Зачастую, регрессия подаётся в виде простого уравнения, которое раскрывает зависимость и силу связи между двумя группами числовых переменных, одна из которых называется зависимой (эндогенной), а вторая - независимой (экзогенной или фактором). Если есть группа взаимосвязанных показателей, то зависимая переменная выбирается логическими размышлениями, а остальные выступают независимыми. То есть, если у нас есть расстояние между городами и затраты на путешествие, то вполне ясно, что затраты будут зависеть от расстояния. Уравнения бывают двух видов: линейные и нелинейные (это уже чистая математика). Стоит рассмотреть каждый из видов.
Линейное уравнение иллюстрирует строго линейную связь между переменными, то есть в нём отсутствуют степени, дроби, тригонометрические функции. Решается стандартными математическими способами.
Уравнение линейной регрессии имеет вид: 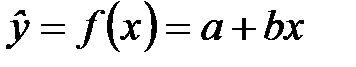 .
.
Логично предположить, что в нелинейный класс уравнений входит всё то, что не вошло в линейный. Решаются такие уравнения сведением к линейному типу, а дальше – по накатанной дорожке.
Уравнения нелинейной регрессии:
¾ полиномиальная функция 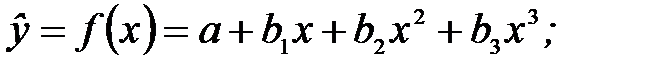
¾ гиперболическая 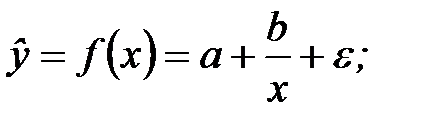
¾ степенная модель 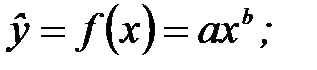
¾ показательная модель 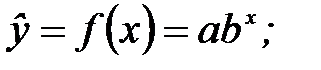
¾ экспоненциальная модель 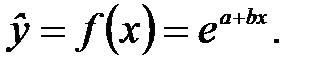
Регрессия бывает двух видов: парная (линейная и нелинейная) и множественная (линейная и нелинейная). Разница между ними в виде уравнения и количестве независимых переменных. Парная регрессия – это, когда одна зависимая переменная и одна независимая, в множественной – независимых переменных несколько. В природе имеет место исключительно множественная регрессия, так как нельзя ограничить внешнее влияние на какое-то явление строго одним фактором.
Парная (её ещё называют двухфакторной) модель проста в использовании, так как имеется всего две переменные: эндогенная и экзогенная. Что позволяет просто решить уравнение и провести анализ.
 2017-12-14
2017-12-14 526
526








