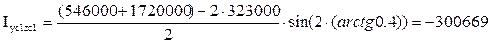Центробежный момент инерции уголка

мм⁴

Центробежный момент инерции всего сечения относительно осей Z_cY_c:

I_yczc= (-300669+(-10)∙(-99)∙1390)+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)

I_yczc= -19761573 мм⁴

Для проверки правильности выбора знака угла b следует разбить уголок на два прямоугольника (рис.3) пересчитать и сравнить их расхождение в центробежном моменте инерции. Если расхождение велико это означает, что угол выбран не с тем знаком.

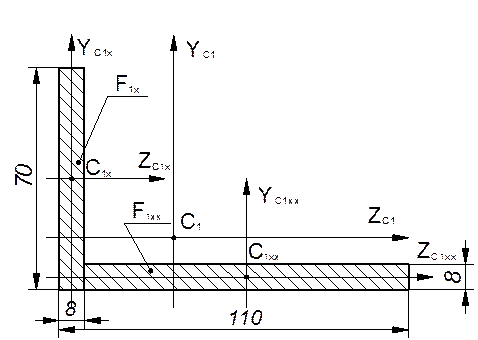
рис.3

Центробежный момент для всего сечения с уголком, разделенным на два простых прямоугольника равен:

F_1x=560 мм² – площадь поперечного сечения

F_1xx=880 мм² – площадь поперечного сечения

a_1x= 8.4 мм – координата от оси Z_c1x до Z_с

b_1x= -131 мм – координата от оси Y_c1x до Y_с

a_1xx= -76 мм – координата от оси Z_c1xx до Z_с

b_1xx= -22.5 мм – координата от оси Y_c1xx до Y_с

I_yczc=(I_yc1zc1+((a_1x∙ b_1x∙F_1x)+(a_1xx∙ b_1xx∙F_1xx)))+(I_yc2zc2+a₂∙ b₂∙F₂)+(I_yc3zc3+a₃∙ b₃∙F₃)

I_yczc= (0+((8.4)∙(-131)∙560)+((-76)∙(-22.5)∙880))+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)

I_yczc= -19785224 мм⁴

Как видно из расчетов центробежные моменты инерции вычисленные разными способами расходятся в значениях не более чем на 0.12%. Это означает, что знак угла α выбран правильно.

3. Нахождение положения главных осей и моментов инерции:

Угол наклона главных осей инерции, проходящих через центр тяжести составного сечения, к центральным осям инерции Z_cY_c определим по формуле:

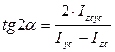
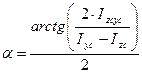
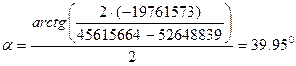
Так как угол a>0, то откладываем его по оси Z против движения часовой стрелки.

Определение величин главных моментов инерции I_u и I_v сечения:

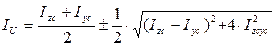
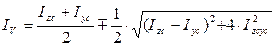
Верхние знаки следует брать при I_zc > I_yc, а нижние I_zc < I_yc

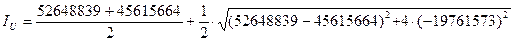= 69204276мм⁴

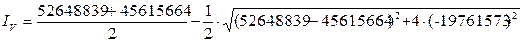= 29060227 мм⁴

Проверка

I_U + I_V = I_zc + I_yc Þ69204276+29060227 = 52648839+45615664 Þ 98264503=98264503

Главная центральная ось U получается на чертеже поворотом оси Z_c против часовой стрелки, так как a>0 и ось U будет являться осью относительно которой момент инерции будет максимальным.

РАЗДЕЛ II

ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЕЙ.

СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ.