Теорема об изменении кинетического момента. Теорема Резаля. Кинетический момент при сложном движении тела. Закон сохранения кинетического момента

1) теорема моментов относительно центра: производная по времени от момента количества движения системы относительно некоторого центра, равна главному моменту действующих на систему внешних сил относительно того-же центра

2) теорема моментов относительно оси: производная по времени от кинетического момента механической системы относительно некоторой оси равна алгебраической сумме моментов, приложенных к системе внешних сил относительно той же оси.

Закон сохранения кинетического момента механической системы:

1)если главный момент внешних сил действующих на систему относительно произвольного центра остаётся равным 0 в процессе движения, то кинетический момент системы относительно этого центра не изменяется:

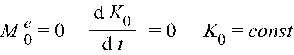
2)если сумма моментов действующих внешних сил относительно какой либо оси координат равна 0, то кинетический момент системы относительно этой оси остаётся постоянным:

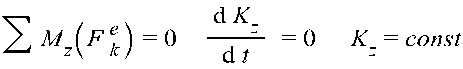
Кинетический момент системы в сложном движении

Наряду с инерциальной системой отсчета с осями xyz введем поступательно движущиеся С координаты с началом в центре масс С (Рис.3). Теперь движение каждой точки можно представить как сложное. Скорость точки будет складываться из переносной скорости, равной для всех точек скорости центра масс С и относительной скорости v_jr

v_j=v_C+v_jr (7)

Кроме того, из рисунка видно, что

r_j=r_C+r_j (8)

Теперь

K_o= S m_j(r_C+r_j)×(v_C+v_rj)=

r_C×v_C S m_j+ r_C×S m_j v_rj+(S m_j r_j)×v_C+S m_j r_j×v_rj (9)