1. Изменить в двойном интеграле 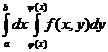 порядок интегрирования
порядок интегрирования
| a | b | 
| 
|
| 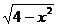
| ||
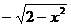
| 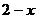
| ||
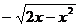
| 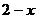
| ||
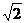
| 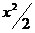
| 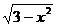
| |
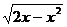
| 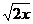
| ||
| 3/2 | 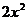
| 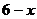
| |
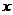
| 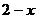
|
2. Вычислить площадь плоской области D, ограниченной
а) прямой 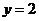 и параболой
и параболой 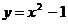 .
.
б) прямыми 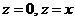 и окружностью
и окружностью 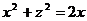
в) кривой 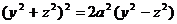
г) кривой 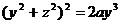
Вычислить объём тела, ограниченного
а) плоскостями 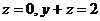 и цилиндром
и цилиндром 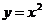
б) плоскостью 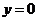 и параболоидом
и параболоидом 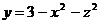
г) Вычислить объём тела, вырезанного цилиндром 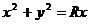 из сферы
из сферы 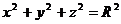
4. С помощью тройного интеграла вычислить объём тела 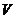 , переходя к цилиндрическим или сферическим координатам
, переходя к цилиндрическим или сферическим координатам
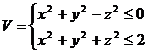
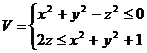
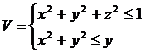
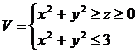
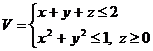
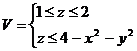
Вычислить площади части поверхности П, заключённую внутри цилиндрической поверхности Ц
1. П: 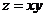 , Ц:
, Ц: 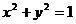 , 2. П:
, 2. П: 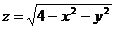 , Ц:
, Ц: 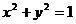 ,
,
3. П: 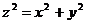 , Ц:
, Ц: 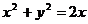 , 4. П:
, 4. П: 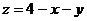 Ц:
Ц: 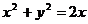 ,
,
5. П: 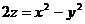 , Ц:
, Ц: 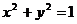 , 6. П:
, 6. П: 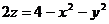 , Ц:
, Ц: 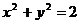 ,
,
Тема 9. Криволинейные и поверхностные интегралы. Элементы теории поля
1. Вычислить двумя способами: непосредственно и по формуле Грина криволинейный интеграл
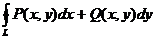 по замкнутому контуру
по замкнутому контуру 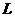 , пробегаемому против часовой стрелки
, пробегаемому против часовой стрелки
| N | L | P(x,y) | Q(x,y) |
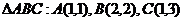
| 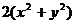
| 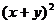
| |
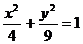
| 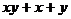
| 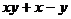
| |
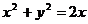
| 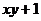
| 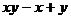
| |
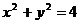
| 
| 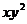
| |
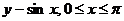
| 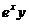
| 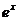
| |
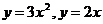
| 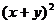
| 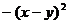
|
2. Найти поток векторного поля 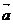 через замкнутую поверхность П двумя способами:
через замкнутую поверхность П двумя способами:
a) непосредственно, вычисляя потоки через все гладкие куски поверхности П
б) по теореме Остроградского-Гаусса
| N | 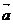
| П |
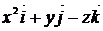
| 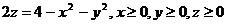
| |
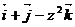
| 
| |
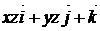
| 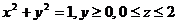
| |
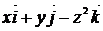
|  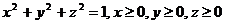
| |
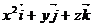
| 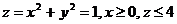
| |
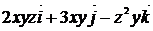
| 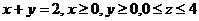
|
3. Найти циркуляцию векторного поля 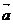 по замкнутому контуру Г двумя способами:
по замкнутому контуру Г двумя способами:
а) непосредственно, вычисляя (криво)линейный интеграл векторного поля по контуру Г
б) по теореме Стокса
| N | 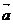
| Г |
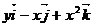
| 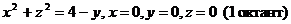
| |
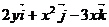
| 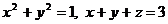
| |
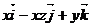
| 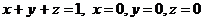
| |
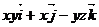
| 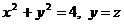
| |
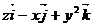
| 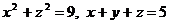
| |
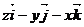
| 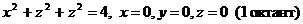
|
Тема 10. Ряды
1. Исследовать на сходимость числовые ряды:
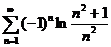 ;
; 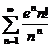 ;
; 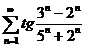 ;
; 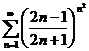 ;
; 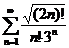 ;
;
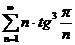 ;
; 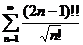 ;
; 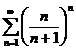 ;
; 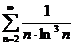 ;
; 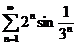 ;
;
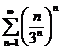 ;
; 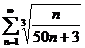 ;
;  ;
; 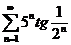 ;
; 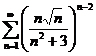 ;
; 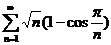 ;
; 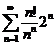 ;
; 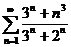 ;
; 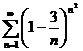 ;
; 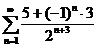 ;
; 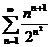 ;
; 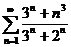 ;
;
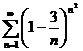 ;
; 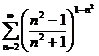 ;
; 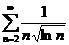 ;
; 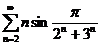 ;
; 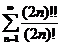 ;
; 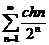 ;
;
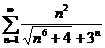 ;
; 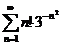 ;
; 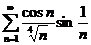 ;
; 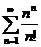 ;
; 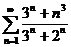 ;
; 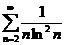 ;
;
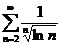 ;
; 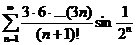 ;
; 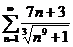 .
. 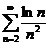 ;
;
1а. Исследовать на сходимость числовые ряды:
(признак сравнения) 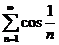 ;
; 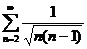 ;
; 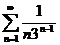 ;
; 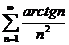 ; (предельный признак сравнения, сходимость рядов с эквивалентными членами)
; (предельный признак сравнения, сходимость рядов с эквивалентными членами) 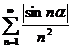 ;
; 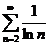 ;
; 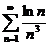 ;
; 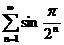 ;
; 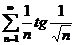 ;
;
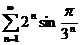 ;
; 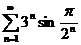 ;
; 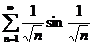 ;
; 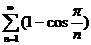 ;
; 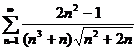 ;
; 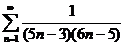 ; (признак Даламбера)
; (признак Даламбера) 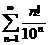 ;
; 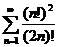 ;
; 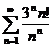 ;
; 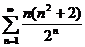 ; (признак Коши)
; (признак Коши) 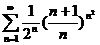 ;
; 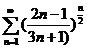 ;
; 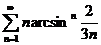 ; (интегральный признак)
; (интегральный признак) 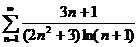 ;
; 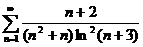 ;
; 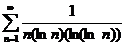 ;
; 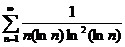 ;
;
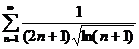 ; (признак Лейбница, указать абсолютную или условную сходимости рядов)
; (признак Лейбница, указать абсолютную или условную сходимости рядов)
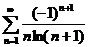 ;
; 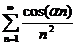 ;
; 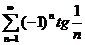 ;
; 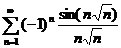 ;
; 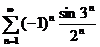 ;
; 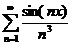 ;
;
2. Разложить данную функцию в ряд Тейлора по степеням (х-х0) и указать радиус сходимости ряда:
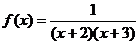 , х0=1;
, х0=1; 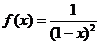 , х0=0; f(x)=ln(1+x-2x2), x0=0;
, х0=0; f(x)=ln(1+x-2x2), x0=0;
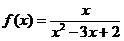 , х0=0;
, х0=0; 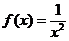 , х0=1;
, х0=1; 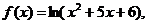 x0=0.
x0=0.
3. Разложить данную функцию в ряд Тейлора по степеням (х-х0) и указать значение 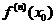 :
:
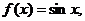
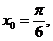 n=28;
n=28; 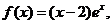
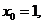 n=7;
n=7; 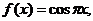
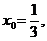 n=21;
n=21; 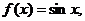
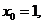 n=19;
n=19; 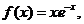
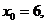 n=17.
n=17.
4. Разложить данную функцию в ряд Тейлора по степеням (х-х0) и указать область сходимости:
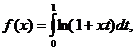
 ;
; 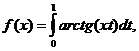
 ;
; 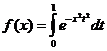 ,
,  ;
;
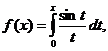
 .
. 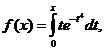
 ;
; 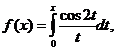
 ;
;
5. Найти интервал сходимости степенного ряда, исследовать поведение ряда на концах интервала сходимости:
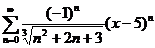 ;
; 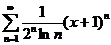 ;
; 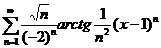 ;
;
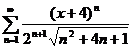 ;
; 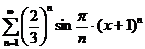 ;
; 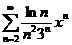 ;
;
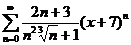 ;
; 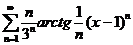 ;
; 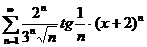
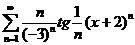 ;
; 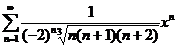 ;
; 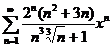
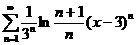 ;
; 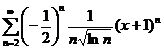 ;
; 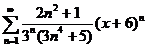
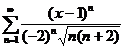 ;
; 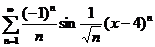 ;
; 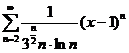
6. Найти область сходимости функционального ряда:
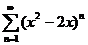 ;
; 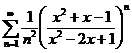 ;
; 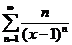 ;
; 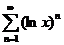 ;
; 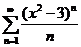 ;
; 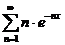
 2017-12-14
2017-12-14 512
512







