Непрерывно-стохастические модели 3 страница

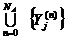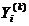Поэтому можно ввести однозначный оператор с областью определения в множестве и областью значений в множестве , сопоставляющий входному контакту выходной контакт , связанный с ним элементарным каналом. Если в А-схеме к контакту не подключен никакой элементарный канал, то оператор R не определен на этом контакте .Оператор R называется оператором сопряжения элементов (агрегатов) в А-схему. Совокупность множеств , и оператор R образуют схему сопряжения элементов в систему S.

Рассмотрим оператор сопряжения для А-схемы, структура кото­рой показана на рис. 2.11. Оператор сопряжения R можно задать в виде таблицы, в которой на пересечении строк с номерами элементов (агрегатов) n и столбцов с номерами контактов i рас­полагаются пары чисел k, l,указывающие номер элемента k и номер контакта l, с которым соединен контакт (табл. 2.7).

Если столбцы и строки такой таблицы пронумеровать двой­ными индексами п, i и k, l, соответственно и на пересечении поме­щать 1 для контактов п, i и к, l,соединенных элементарным каналом и 0 в противном случае, то получим матрицу смежности ориен­тированного графа, вершинами которого являются контакты аг­регатов, а дугами — элементарные каналы А-схемы.

Рассмотренная схема сопряжения агрегатов в А-схему,заданная совокупностью множеств , и оператором R,является одноуровневой схемой сопряжения. В более сложных случаях могут быть использованы многоуровневые иерархические схемы сопряже­ния. Схема сопряжения агрегата, определяемая оператором R, мо­жет быть использована для описания весьма широкого класса объектов. Однако взаимодействие элементов реальных систем даже в рамках механизма обмена сигналами не сводится к одному лишь сопряжению. Помимо сопряжения контактов серьезную роль игра­ют также согласование совокупности элементарных сигналов, по­ступающих в элементарный канал от выходных контактов и воспри­нимаемых входными, а также влияние реальных средств передачи сигналов на их содержание. Кроме того, оказываются полезными некоторые дополнительные ограничения на структуру сопряжения агрегатов системы S с внешней средой Е. Поэтому с практической точки зрения представляет интерес понятие А-схемы как типовой ма­тематической, отражающей наши представления о взаимодействии реальных объектов в рамках механизмов обмена сигналами.

 

Таблица 2.7

	1,1 0,1 1,3 1,2 3,2 2,2 5,2	3,1   0,2 2,1 2,1   0,4	4,1   0,3   2,2	5,1	6,1

 

Упорядоченную совокупность конечного числа агрегатов , системы S, агрегата , характеризующего внешнюю среду Е,и оператора R,реализующего отображение , будем называть А-схемой при следующих условиях:

1) для любых и в данной А-схеме ;

2) если , то

, (2.18)

где — соответствующие множества элементарных сигналов; для любого момента t' выдачи непустого элементарного сигнала

, (2.19)

имеет место

, (2.20)

, (2.21)

где .

Ограничение (2.18) относится к структуре сопряжения агрегатов А-схемы системы S с внешней средой Е и требует, чтобы каждый элементарный канал, передающий сигналы во внешнюю среду, начинался в одном из выходных контактов одного из агрегатов системы, каждый элементарный канал, передающий сигналы из внешней среды, заканчивался на одном из входных контактов А-схемы. Ограничение (2.19) предусматривает, что сигналы в А-схеме передаются непосредственно от одного агрегата к другому без устройств, способных отсеивать сигналы по каким-либо признакам. Ограничение (2.20) относится к согласованию функционирования агрегатов А-схемы во времени. Ограничение (2.21) предусматривает, что сигналы между агрегатами А-схемы передаются мгновенно, без искажений и перекодирования, изменяющего структуру сигнала. Для многих реальных систем ограничения (2.19) и (2.21) оказывают­ся несправедливыми. Для того чтобы А-схема была адекватной моделью реального объекта, достаточно описать селектирующие устройства, реальные средства передачи сигналов и всевозможные вспомогательные устройства как самостоятельные агрегаты, связи между которыми удовлетворяют перечисленным ограничениям.

 

Пример 2.11. Рассмотрим представление некоторой системы в виде отдельного агрегата [4]. Для того чтобы упростить описание объекта моделирования и просле­дить связи с уже рассмотренными схемами, воспользуемся в качестве объекта такого моделирования схемой массового обслуживания (Q-схемой)и представим ее в виде агрегата (А-схемы).Для определенности полагаем, что имеется однофазная одноканальная система ,показанная на рис. 2.6. В моменты времени , образующие однородный поток случайных событий, в прибор (П) поступают заявки, каждая из которых характеризуется случайным параметром . Если обслуживающий канал (К) занят, то заявка поступает в накопитель (Н) и может ждать там не более чем , где h — параметр, характеризующий производительность системы обслуживания. Если к моменту заявка не будет принята к обслуживанию, то она теряется. Время обслуживания заявки .

При представлении этой Q-схемы в виде А-схемы опишем ее состояния вектором со следующими компонентами: — время, оставшееся до окончания обслуживания заявки, которая находится в канале (К); — количество заявок в приборе (П); , где — параметр k -йзаявки в накопителе (H); оставшееся время ожидания k -й заявки в накопителе (Н) до момента, когда она получит отказ, , , .

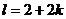Входные сигналы (заявки) поступают в А-схему в моменты и принимают значения . Рассмотрим случайные операторы V, U и G,описывающие такой агрегат. Пусть в момент поступает новая заявка. Тогда оператор V можно записать следующим образом:

Пусть 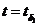,т. е. обслуживание очередной заявки окончено. Этот момент является особым, так как в этот момент достигает , т. е. . Поэтому скачок состояний определяется оператором вида

Рассмотрим еще один особый момент времени ,не являющийся моментом поступления входного сигнала. В момент , когда истекает время ожидания одной из заявок, например i -й, число заявок в системе уменьшается на 1. Состояние А-схемы определяется оператором вида

В полуинтервалах между особыми моментами времен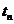и и , к которым относятся моменты поступления в А-схему входных сигналов и выдачи выходных сигналов, состояния А-схемы изменяются по закону, задаваемому опера­тором U,который можно записать так:

Выходными сигналами А-схемы будем считать сведения о заявках, покидающих прибор (П). Пусть , где — признак (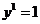, если заявки обслужены; , если заявки не обслужены); — совокупность сведений о заявке, например , т. е. заявки поступили в систему обслуживания с параметром , обслуживались при значении параметра системы , покинули систему в момент . Таким образом, действия оператора G сводятся к выбору признака и формированию сведений о заявке . Для моментов и выходной сигнал у определяется параметром G и может быть записан в следующем виде:

где находят из , a — из .

На основания состояний системы можно оценить ее вероятностно-временные характеристики, например вероятность нахождения в обслуживающем приборе (П) заданного числа заявок, среднее время ожидания заявок в накопителе (Н) и т. д.

 

Таким образом, дальнейшее использование обобщенной типо­вой математической схемы моделирования, т. е. А-схемы, в принци­пе не отличается от рассмотренных ранее D-, F-, Р-, N-, Q-схем. Для частного случая, а именно для кусочно-линейных агрегатов, резуль­таты могут быть получены аналитическим методом. В более слож­ных случаях, когда применение аналитических методов неэффектив­но или невозможно, прибегают к имитационному методу, причем представление объекта моделирования в виде А-схемы может яв­ляться тем фундаментом, на котором базируется построение ими­тационной системы и ее внешнего и внутреннего математического обеспечения. Стандартная форма представления исследуемого объекта в виде А-схемы приводит к унификации не только алгорит­мов имитации, но и к возможности применять стандартные методы обработки и анализа результатов моделирования системы S.

Рассмотренные примеры использования типовых математичес­ких схем (D-, F-, Р-, Q-, N-, А-схем)позволяют формализовать достаточно широкий класс больших систем, с которыми приходится иметь дело в практике исследования и проектирования сложных систем. Особенности и возможности применения типовых схем при разработке машинных моделей систем рассмотрены в гл. 8 и 10.

 

Контрольные вопросы

 

2.1.Что называется математической схемой?

2.2.Что является экзогенными и эндогенными переменными в модели объекта?

2.3.Что называется законом функционирования системы?

2.4.Что понимается под алгоритмом функционирования?

2.5.Что называется статической и динамической моделями объекта?

2.6.Какие таловые схемы используются при моделировании сложных систем и их элементом?

2.7.Каковы условия и особенности использования при разработке моделей систем различных типовых схем?

 

 

ГЛАВА III

ДИСПЕРСИОННЫЙ АНАЛИЗ

 

1. Задача дисперсионного анализа. Влюбом эксперименте средние значения наблюдаемых величин меняются в связи с изменением основных факторов (качественных и количественных), определяющих условие опыта, а также и случайных факторов. Исследование влияния техили иных факторов на изменчивость средних является задачей дисперсионного анализа.

В дисперсионном анализе используется рассмотренное в гл. 1,3 свойство аддитивности дисперсии изучаемой случайной величины, обусловленной действием независимых факторов. Р. А. Фишер в 1938 г. впервые определил дисперсионный анализ как «отделение дисперсии, приписываемой одной группе причин, от дисперсии, приписывае­мой другим группам». В зависимости от числа источников дисперсии различают однофакторный и многофакторный дисперсионный анализ.

Дисперсионный анализ особенно эффективен при изучении не­скольких факторов. При классическом методе исследования варьируют только один фактор, а остальные оставляют постоянными. При этом для каждого фактора проводится своя серия наблюдений, не используемая при изучении других факторов. Кроме того, при таком методе исследования не удается определить взаимодействие факторов при одновременном их изменении. При дисперсионном анализе каждое наблюдение служит для одновременной оценки всех факторов и их взаимодействий.

Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость изучаемой случайной величины. Для этого производится разложение суммарной выборочной дисперсии на составляющие, обусловленные независимыми факторами. Каждая из этих составляющих представляет собой оценку дисперсии генераль­ной совокупности. Чтобы решить, значимо ли влияние данного фактора, необходимо оценить значимость соответствующей выборочной дисперсии в сравнении с дисперсией воспроизводимости, обусловлен­ной случайными факторами. Проверка значимости оценок дисперсий проводится по критерию Фишера (см. гл. II, 11). Если рассчитанное значение критерия Фишера окажется меньше табличного, то влияние рассматриваемого фактора нет оснований считать значимым. Если же рассчитанное значение критерия Фишера окажется больше таблич­ного, то рассматриваемый фактор влияет на изменчивость средних. В дальнейшем будем полагать, что выполняются следующие допуще­ния: 1) случайные ошибки наблюдений имеют нормальное распреде­ление; 2) факторы влияют только на изменение средних значений, а дисперсия наблюдений остается постоянной; эксперименты равноточны.

Требование нормального распределения определяет выбор основ­ных факторов при исследовании процесса методом дисперсионного анализа. Если нужно получить нормальное распределение выходной величины, к случайным желательно относить только те факторы, влияние которых на выходную величину очень мало. Исключение можно делать лишь для тех факторов, которые сами по себе (из каких-либо других соображений) дают нормальное распределе­ние результатов.

Факторы, рассматриваемые в дисперсионном анализе, бывают двух родов: 1) со случайными уровнями и 2) с фиксированными. В первом случае предполагается, что выбор уровней производится из бесконечной совокупности возможных уровней и сопровождается рандомизацией. При этом результаты эксперимента имеют большеезначение, поскольку выводы по эксперименту можно распространить на всю генеральную совокупность. Если все уровни выбираются случайным образом, математическая модель эксперимента называется моделью со случайными уровнями факторов (случайная модель). Когда все уровни фиксированы, модель называется моделью с фиксирован­ными уровнями факторов. Когда часть факторов рассматривается на фикси­рованных уровнях, а уровни остальных выбираются случайным образом, модель называется моделью смешанного типа. Иногда отсутствует различие в критериях, применяемых для разных моделей, и единствен­ное различие состоит в общности выводов, в других случаях существует различие в критериях.

Дисперсионный анализ может применяться в различных формах в зависимости от структуры исследуемого процесса; выбор соответ­ствующей формы является обычно одной из главных трудностей в практическом применении анализа.

2. Однофак т орный дисперсионный анализ. Рассмотрим действие единичного фактора А (количественного или качественного), который принимает k различных значений (уровней фактора). На i -м уровне производится 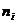наблюдений, результаты которых можно записать следующим образом:

Будем предполагать, что результат любого наблюдения можно представить в виде модели

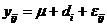(III.1)

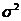где —суммарный эффект во всех опытах; — эффект фактора А на i -м уровне (i =1,2..., k); —ошибка измерения на i -м уровне. Предположим также, что наблюдения на фиксированном уровне фактора нормально распределены относительно среднего значения общей дисперсией . Общее число опытов равно N:

(III.2)

Проверяется нулевая гипотеза равенства средних значений на раз­личных уровнях фактора А:

Наиболее простые расчеты получаются при равном числе опытов на каждом уровне фактора А: (табл. 5).

При этом общее число наблюдений N равно kп. Обозначим через y среднее значение наблюдений на i -м уровне

(III.3)

 

Таблица 5. Исходные данные для однофакторного дисперсионного анализа сравнымчислом повторений опытов

Номер наблюдений	Уровни фактора А
		…
. . . n	. . .	. . .		. . .
Итоги

 

а общее среднее значение для всей выборки из N наблюдений

(III.4)

Для проведения дисперсионного анализа необходимо общую выбороч­ную дисперсию

(III.5)

разложить на составляющие, которые характеризовали бы вклад фак­тора А и фактора случайности. Фактор случайности при этом легко оценить благодаря наличию повторных опытов на каждом уровне. Определим выборочную дисперсию на каждом уровне:

(III.6)

 

Если нет уверенности в равноточности экспериментов, однородность дисперсий можно проверить по критерию Кохрена (см. гл. 11,13).

Если между дисперсиями нет значимых различий, для оценки генеральной дисперсии 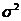, характеризующей фактор случайности, используют выборочную дисперсию :

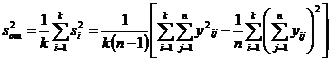(III.7)

Число степеней свободы дисперсии равно . При­ближенную оценку для дисперсии фактора А можно получить следую­щим образом:

(III.8)

Более точную оценку для можно получить, рассматривая отклоне­ния средних на отдельных уровнях от общего среднего всей выборки .Действительно,

(III.9)

Отсюда

(III.10)

Дисперсия фактора А для модели с фиксированными уровнями не связана ни с какой случайной величиной, это условное название для математического ожидания среднего квадрата отклонений, обусловленного влиянием фактора А. Такое обозначение удобно, так как определяет рассеяние, вызванное влиянием фактора А анало­гично показателю влияния случайного фактора, что позволяет не­посредственно сравнить фактор А с эффектом случайности. Введем также следующее обозначение:

(III.11)

Эта дисперсия имеет степеней свободы. Если дисперсия 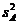значимо отличается от 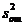, нулевая гипотеза от­вергается и влияние фактора А считается существенным. Проверяет­ся нулевая гипотеза по критерию Фишера. Так как альтернативой 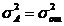, является неравенство 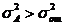, для проверки гипотезы применя­ется односторонний критерий Фишера. Влияние фактора А считается значимым, если