Непрерывно-стохастические модели 5 страница

принимается гипотеза 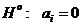. Если

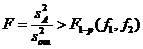(III.42)

нулевая гипотеза отвергается и влияние фактора А считается значи­мым. Аналогично, если

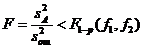
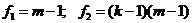(III.43)

принимается гипотеза 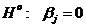. При справедливости неравенства

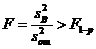(III.44)

влияние фактора В считается значимым. При проверке нулевых гипо­тез применяется односторонний критерий Фишера, так как альтерна­тивой равенству 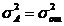служит неравенство 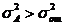. При проведении дисперсионного анализа в условиях линейной модели (III.29) удобно использовать следующий алгоритм расчета. Находят: 1)итоги по столбцам

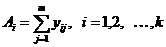(III.45)

2)итоги по строкам

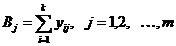(III.46)

3) сумму квадратов всех наблюдений

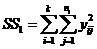(III.47)

4) сумму квадратов итогов по столбцам, деленную на число
наблюдений в столбце,

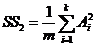(III.48)

5) сумму квадратов итогов по строкам, деленную на число наблюденийв строке,

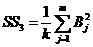(III.49)

6) квадрат общего итога, деленный на число всех наблюдений (коррек­тирующий член),

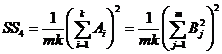(III.50)

7)сумму квадратов для столбца

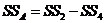(III.51)

8)сумму квадратов для столбца

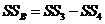(III.52)

9) общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом,

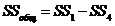(III.53)

10) остаточную сумму квадратов

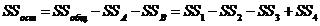(III.54)

11) дисперсию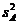

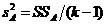(III.55)

12) дисперсию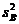

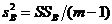(III.56)

13) дисперсию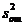

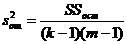(III.57)

Результаты расчета удобно представлять в виде табл. 9.

 

 

Таблица 9. Двухфакторный дисперсионный анализ (без повторения опытов)

Источник дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат	Математическое ожидание среднего квадрата
A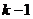
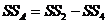
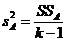
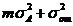
B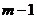
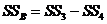
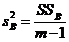
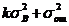
Остаток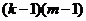
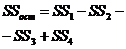
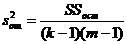
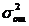
Общая сумма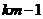

 

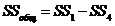
Установив при помощи дисперсионного анализа значимость влияния данного фактора, выясняют затем при помощи критерия Стьюдента или рангового критерия Дункана, какие именно средние значения y различны.

Линейная модель (III.29) справедлива, если между факторами А и В нет взаимодействия. В противном случае этому взаимодействию как факторуприсуща своя дисперсия 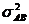. Взаимодействие АВ, 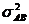служит мерой того, насколько влияние фактора А зависит от уровня фактора В,и наобо­рот, насколько влияние фактора В зависит от уровня А. В приведенном алгоритме при наличии взаимодействия между факторами 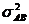, как со­ставная часть, входит в дисперсию 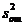. Выделить 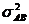можно только при наличии параллельных наблюдений.

Пусть при каждом сочетании уровней факторов А и В проводится п параллельных опытов. Так, в табл. 7 в ячейке, образованной пере­сечением i -го столбца и j -й строки, имеется целая серия наблюдений 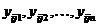. Сохраним обозначение 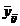за средним результатом в ячейке. Выборочная дисперсия результатов в каждой ячейке

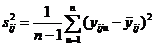(III.58)

имеет 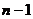степень свободы. Если выборочные дисперсии по всем ячейкам однородны, их можно усреднить и использовать полученную средневзвешенную дисперсию

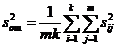(III.59)

в качестве оценки для дисперсии воспроизводимости 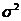. Число степеней свободы 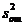равно 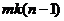. Более удобная формула для вычисления дисперсии воспроизводимости

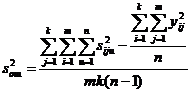(III.60)

где 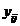— сумма наблюдений в ij -йячейке.

При проведении дисперсионного анализа для нелинейной модели удобно использовать следующий алгоритм расчета. По табл. 7 находят:

1)суммы наблюдений в каждой ячейке

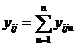(III.61)

2)квадрат сумм наблюдений в каждой ячейке

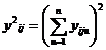(III.62)

3) итоги по столбцам

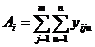(III.63)

4)итоги по строкам

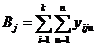(III.64)

5)сумму всех наблюдений (общий итог)

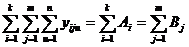(III.65)

6)сумму квадратов всех наблюдений

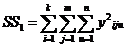(III.66)

7)сумму квадратов итогов по столбцам, деленную на число наблюде­ний в столбце,

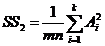(III.67)

8)сумму квадратов итогов по строкам, деленную на число наблюде­ний в строке,

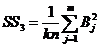(III.68)

9)квадрат общего итога, деленный на число всех наблюдений (коррек­тирующий член),

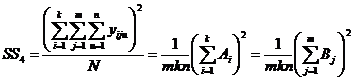(III.69)

10)сумму квадратов для столбца

(III.70)

11)сумму квадратов для строки

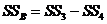(III.71)

12)сумму квадратов для дисперсии воспроизводимости

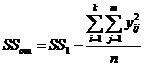(III.72)

13)общую сумму квадратов, равную разнице между суммой квадра­тов всех наблюдений и корректирующим членом,

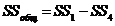(III.73)

14)остаточную сумму квадратов отклонений для эффекта взаимо­действия

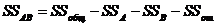(III.74)

15) дисперсию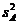

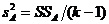(III.75)

16) дисперсию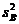

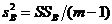(III.76)

17) Дисперсию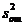

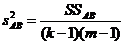(III.77)

18) дисперсию воспроизводимости

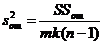(III.78)

Проверка гипотезы о значимости взаимодействия факторов А и В проводится по F -критерию одинаково для моделей со случайными и фиксированными уровнями. Однако проверки гипотез о значимости факторов А и В проводят неодинаково для разных моделей. В табл. 10 приведен двухфакторный дисперсионный анализ с повторными опытами для модели со случайными уровнями.

 

Таблица 10. Двухфакторный дисперсионный анализ для модели со случайными уровнями (с повторными опытами)

Источник дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат	Математическое ожидание среднего квадрата
A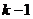
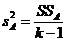
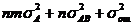
B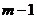
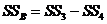
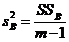
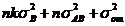
AB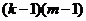
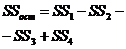
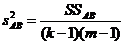
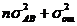
Остаток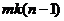
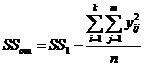
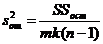
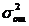
Общая сумма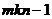

 

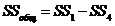
Из табл. 10 видно, что для оценки значимости фактора А необходимо составить дисперсионное отношение вида

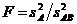(III.79)

Влияние фактора Л признается значимым, если

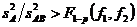(III.80)

где p —уровень значимости; 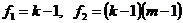. Аналогично, влияние фактора В считается значимым, если

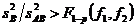(III.80 a)

Если неравенства (III.80) и (III.80 а) не выполняются, влияние фак­торов А и В следует считать незначимым.

Для математической модели с фиксированными уровнями члены, соответствующие взаимодействию, исчезают из сумм квадратов откло­нени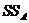й и .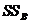

Вследствие этого для оценки значимости фактора А составляют дис­персионное отношение вида

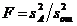(III.81)

в знаменателе которого стоит оценка дисперсии воспроизводимости. Полученное дисперсионное отношение сравнивается с табличным 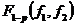для чисел степеней свободы 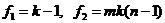. Ана­логично, для оценки фактора В рассматривают отношение

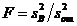(III.81 a)

которое сравнивают с табличным 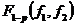для чисел степеней свободы 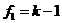и .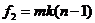

Если дисперсионные отношения (III.81) и (III.81 a) больше табличных

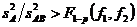
и (III.81 б)

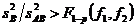
влияние факторов А и В следует считать значимым. Если же неравен­ства (III.81 6) не выполняются, влияние факторов А и В незначимо. Для проверки значимости эффекта взаимодействия составляют диспер­сионное отношение вида

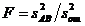
и сравнивают его с табличным 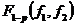при уровне значимости р и числах степеней свободы 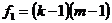и 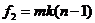.Если получен­ное дисперсионное отношение больше табличного 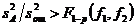, влияние эффекта взаимодействия факторов надо считать значимым. В противном случае, если 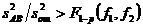, влияние эффекта взаимо­действия следует считать незначимым.

 

Пример 2. Исследовалось влияние на процесс органического синтеза двух факто­ров: А — тип растворителя на уровнях 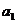, , 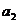, 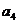и В — тип галогеналкила на уровнях 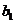, , 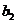, 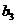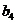. Результаты (выход полимера в процентах) представлены в таблице:

 

B	A
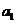
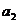
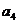
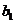
	13,2 13,9	4,7 5,8	53,4 48,3	13,6 13,2
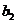
	18,9 21,0	19,8 17,9	14,0 13,2	9,5 8,6
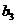
	7,3 8,5	38,2 37,7	5,1 5,9	54,4 55,2
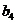
	20,0 20,8	60,1 60,9	19,6 18,5	58,2 59,7

 

При каждом сочетании типа растворителя и галогеналкила сделано два параллель­ных опыта. Требуется оценить значимость влияния типа растворителя и галогеналкила на процесс синтеза.

Решение. Математическая модель эксперимента представляет собой модель с фиксированными уровнями. Уровни факторов А и В выбраны не случайно, поскольку необходимо установить влияние на процесс синтеза только данных четырех типов растворителей и галогеналкилов. Расчет проводится в соответствии с приведенным алгоритмом по формулам (III.61) — (III.78):

1. Определим суммы наблюдений в каждой ячейке (таблица).

 

B	A	Итоги
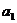
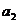
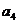
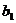
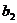
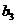
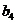
	27,1 39,1 15,8 40,8	10,5 37,7 75,9	101,7 27,2 11,0 38,1	26,8 18,1 109,6 117,9	166,1 122,1 212,3 317,8
Итоги	122,8	245,1	178,0	272,4	818,3

 

2. Возведем полученные суммы в квадрат. Результаты 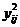представим в виде таб­лицы:

 

B	A
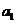
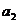
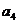
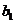
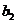
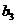
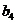
	734,41 1528,81 249,64 1064,64	110,25 1421,29 5760,81	10342,89 739,84 121,0 1451,61	718,24 327,61 12012,16 13900,41

 

3. Подсчитаем итоги по столбцам. Например,

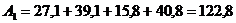
4.Подсчитаем итоги по строчкам. Например,

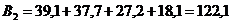
5. Определим общий итог — сумму всех наблюдений:

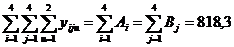
6. Определим сумму квадратов всех наблюдений:

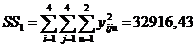
7. Определим сумму квадратов итогов по столбцам, деленную на число наблюде­ний в столбце,

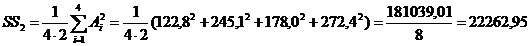
8. Определим сумму квадратов итогов по строкам, деленную на число наблюдений в строке,

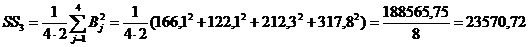
9. Определим квадрат общего итога, деленный на число всех наблюдений.

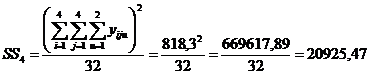
10. Определим суммы квадратов отклонений для факторов А и В:

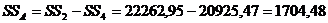
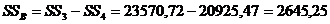
11. Определим сумму квадратов для дисперсии воспроизводимости:

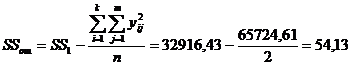
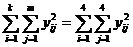
12. Определим общую сумму квадратов;

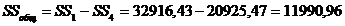
13. Определим сумму квадратов отклонений для эффекта взаимодействия;

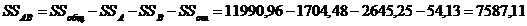
14.Определим соответствующие дисперсии;

 

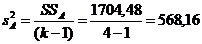
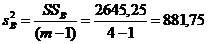
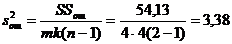
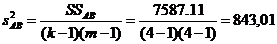
Результаты расчета сведены в таблицу двухфакторного дисперсионного анализа.

 

 

Источник дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат
A B AB Ошибка Общая сумма		1704,48 2645,25 7587,11 54,13 11990,97	568,16 881,75 843,01 3,38

 

Значимость линейных эффектов А и В иэффекта взаимодействия проверялась по критерию Фишера. Дисперсионное отношение для эффекта А

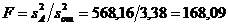
Для эффекта В

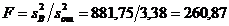
Табличное значение критерия Фишера для уровня значимости 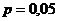и числа сте­пеней свободы 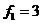и .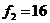

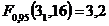Поскольку рассчитанные дисперсионные отношения больше табличного, факторы A и В значимы, т.е. выход полимера существенно зависит от типа растворителя и галогеналкила. Для проверки значимости эффекта взаимодействия составлено отношение

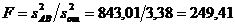
Табличное значение критерия Фишера для 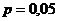, 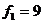и .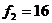

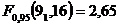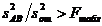
и, следовательно, эффект взаимодействия следует считать значимым. Таким образом, интенсивность влияния типа растворителя на процесс полимеризации зависит от того, с каким галогеналкилом проводится полимеризация, и наоборот, влияние галогеналкила зависит от выбранного растворителя.

 

4. Планирование эксперимента при дисперсионном анализе. Латинские и гипер-греко-латинские квадраты. При изучении влияния на процесс двух факторов число необходимых экспериментов N (без повторения опытов) определялось произведением уровней изучаемых факторов. Если число уровней n одинаково, то объем эксперимента при двух-факторном дисперсионном анализе равен 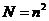. При таком числе опытов в эксперименте встречаютсявсе возможные сочетания уровней изучае­мых факторов. Такой эксперимент называется полным факторным экспе­риментом (ПФЭ). Эксперимент, в котором пропущены некоторые сочета­ния уровней, называется дробным факторным экспериментом (ДФЭ).

Сокращение перебора уровней всегда приводит к потере части ин­формации. Поэтому при ДФЭ важно так спланировать эксперимент, чтобы терялась наименее существенная при данной постановке задачи информация. Особенно широко используется ДФЭ, в котором теряется лишь информация о взаимодействиях изучаемых факторов. Это право­мерно в тех случаях, когда эффекты взаимодействия заведомо отсутству­ют или настолько малы, что их можно не учитывать. Рассмотрим трехфакторный дисперсионный анализ при одинаковом числе уровней п для каждого фактора. Полный перебор сочетаний уровней факторов потре­бует N опытов