
Табличное значение критерия Фишера для уровня значимости  и чисел степеней свободы сравниваемых дисперсий
и чисел степеней свободы сравниваемых дисперсий  и
и 
Сравнение полученных дисперсионных отношений с табличным значением критерия Фишера показывает, что влияние факторов А и С следует признать незначимым. Значимо влияет на процесс только фактор В,так как

Проранжируем эффекты фактора В на разных уровнях при помощи множественного рангового критерия Дункана (см. гл. II, 14). Средние значения выхода полимера для различных типов растворителя:
Тип растворителя 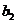
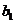
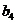
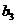
 ........
........ 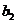
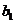
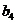
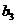
Расположим средние в порядке возрастания:
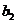
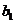
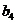
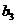




Дисперсия воспроизводимости  с числом степеней свободы
с числом степеней свободы  (см. табл. на с. 101).
(см. табл. на с. 101).
Определим нормированную ошибку среднего:

Выпишем из табл. 7 приложения значимые ранги для  и
и  :
:
Ранги, 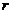 ...... 3,46 3,58 3,64
...... 3,46 3,58 3,64
 ...... 21,4 21,9 22,3
...... 21,4 21,9 22,3
Определив разницу между средними, оценим значимость различия между растворителями:
 - различие значимо
- различие значимо
 - различие значимо
- различие значимо
 - различие незначимо
- различие незначимо
 - различие значимо
- различие значимо
 - различие незначимо
- различие незначимо
 - различие незначимо
- различие незначимо
Приведенный дисперсионный анализ справедлив в условиях линейной модели. Однако, не имея параллельных (повторных) наблюдений, нельзя проверить адекватность принятой линейной модели. Если в каждой ячейке латинского квадрата проделать одинаковое число параллельных опытов, это позволит оценить значимость взаимодействий между факторами. При этом наличие параллельных наблюдений используется только для оценки ошибки опыта. Если эффекты взаимодействия незначимы (линейная модель), то остаточная дисперсия незначимо отличается отдисперсии случайности, обусловленной ошибкой опыта. При этом значимость линейных эффектов может быть легко проверена. Если же линейная модель неадекватна и существуют взаимодействия между факторами, невозможно оценить значимость линейных эффектов, так как все они смешаны с эффектами взаимодействия. В этом случае плодотворным может оказаться выдвижение дополнительных гипотез о незначимости некоторых взаимодействий.
Планирование эксперимента по латинскому квадрату позволяет ввести в исследование три фактора. Для четырех факторов хорошими свойствами обладает план эксперимента по схеме греко-латинского квадрата. Задача состоит в том, чтобы к трем исследуемым факторам, не меняя общего числа опытов n, добавить четвертый фактор D. Это удастся сделать, если найти такое расположение уровней факторов C и D, при котором в каждой строке и в каждом столбце имеются все n уровней фактора С и все n уровней фактора D и в то же время никакие два уровня факторов С и D не встречаются во всей таблице больше одного раза. Расположение такого типа называется латинским квадратом второго порядка, который получается комбинацией двух ортогональных латинских квадратов.
Рассмотрим следующие два латинских квадрата, составленных соответственно из латинских и греческих букв:

 (III.102)
(III.102)
Если наложить эти два латинских квадрата один на другой и составить третий квадрат, каждая клетка которого содержит как латинскую, так и греческую букву соответствующих клеток исходных квадратов, то получим
 (III.103)
(III.103)
В полученном квадрате каждая буква одного квадрата связана один и только один раз с каждой буквой другого квадрата. Такие два латинских квадрата называются ортогональными. Полученный квадрат второго порядка называют также греко-латинским квадратом. Задача о нахождении ортогональных латинских квадратов в комбинаторной математике еще полностью не решена. Доказано существование ортогональных латинских квадратов для n = 3, 4, 5, 7, 8 и 9. Известно, что их нет для  . Для
. Для  поэтому можно построить обычный латинский квадрат и нельзя построить квадрат второго порядка. Латинский квадрат для
поэтому можно построить обычный латинский квадрат и нельзя построить квадрат второго порядка. Латинский квадрат для  не исследован. Если имеется
не исследован. Если имеется  попарно ортогональныхлатинских квадратов, то они образуют так называемую полную систему ортогональных латинских квадратов. Показано, что существуют полные системы латинских квадратов для
попарно ортогональныхлатинских квадратов, то они образуют так называемую полную систему ортогональных латинских квадратов. Показано, что существуют полные системы латинских квадратов для  (p — простое число) и
(p — простое число) и  (степени простого числа). Полную систему ортогональных латинских квадратов для
(степени простого числа). Полную систему ортогональных латинских квадратов для  (p — простое число) можно построить, используя поля Галуа. Построим, например, поле Галуа вычетов по модулю 5. Два целых числа a и b конгруэнтны по модулю 5; если
(p — простое число) можно построить, используя поля Галуа. Построим, например, поле Галуа вычетов по модулю 5. Два целых числа a и b конгруэнтны по модулю 5; если  , где
, где  — какое-либо целое число, это можно записать в виде
— какое-либо целое число, это можно записать в виде
 (III.104)
(III.104)
Конгруэнция (III.104) определяет поле. В этом поле содержится пять различных элементов 0, 1, 2, 3, 4. Составим таблицу сложения и таблицу умножения в этом поле:
Сложение Умножение

 (III.105)
(III.105)
Рассмотрим латинский квадрат, образованный таблицей сложения. Если в этом квадрате заменить p -юстроку, начинающуюся с элемента p (р =0, 1, 2, 3, 4), строкой, полученной прибавлением (по модулю 5) к элементам первой строки первого квадрата числа  , получим второйквадрат:
, получим второйквадрат:

 (III.106)
(III.106)
Для получения p -йстроки третьего и четвертого латинских квадратов прибавляют (по модулю 5) к элементам первой строки первого квадрата соответственно числа  и
и  :
:


 (III.107)
(III.107)

Таким образом, получили полную систему ортогональных латинских квадратов.
Таблица 16. Греко-латинские квадраты

| A | B | ||
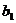
| 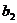
| 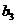
| |
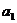
| 
| 
| 
|
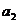
| 
| 
| 
|

| 
| 
| 
|

| A | B | |||
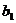
| 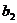
| 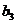
| 
| |
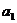
| 
| 
| 
| 
|
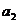
| 
| 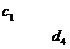
| 
| 
|

| 
| 
| 
| 
|
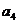
| 
| 
| 
| 
|
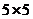
| A | B | ||||
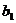
| 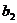
| 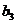
| 
| 
| |
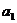
| 
| 
| 
| 
| 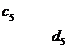
|
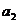
| 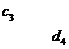
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
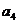
| 
| 
| 
| 
| 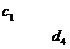
|

| 
| 
| 
| 
| 
|
Планирование эксперимента по схеме греко-латинского квадрата применяется для четырех факторов. Число уровней для всех факторов должно быть одинаково. В табл. 16 приведены греко-латинские квадраты размерности  ,
,  и
и 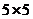 .
.
Греко-латинский квадрат является частью четырехфакторного плана—по схеме греко-латинского квадрата вводятся в план эксперимента факторы С и D Например, в последнем плане (табл. 16) уровни фактора С соответствуют латинским, а уровни фактораD—греческим буквам греко-латинского квадрата (III. 103):  ,
,  ,
,  ,
,  ,
,  и
и  ,
,  ,
,  ,
,  ,
,  . Однако принято греко-латинским квадратом называть весьчетырехфакторный план (табл. 16). Матрица планирования, соответствующая греко-латинскому квадрату
. Однако принято греко-латинским квадратом называть весьчетырехфакторный план (табл. 16). Матрица планирования, соответствующая греко-латинскому квадрату  , приведена в табл. 17.
, приведена в табл. 17.
Таблица 17. План эксперимента  ,
, 
| Номер опыта | A | B | C | D | y | Номер опыта | A | B | C | D | y |
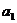
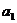
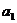
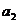
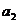
|
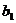
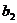
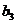
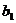
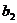
|
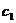
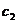
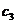
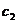
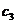
|


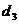
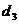

|


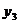


| 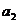



| 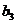
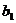
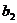
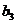
| 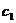
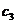
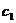
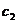
| 

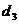

| 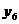



|
Таблица 18. Гипер-греко-латинский квадрат четвертого порядка
| A | B | ||||

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
|
В греко-латинском квадрате имеется 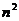 различных комбинаций уровней факторов вместо
различных комбинаций уровней факторов вместо  комбинаций полногочетырехфакторного эксперимента. Поэтому греко-латинский квадрат представляет собой
комбинаций полногочетырехфакторного эксперимента. Поэтому греко-латинский квадрат представляет собой  реплику от полного факторного эксперимента (ПФЭ). Так, приведенный в табл. 16 греко-латинский квадрат
реплику от полного факторного эксперимента (ПФЭ). Так, приведенный в табл. 16 греко-латинский квадрат  представляет собой
представляет собой  реплику от ПФЭ
реплику от ПФЭ 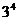
 , греко-латинский квадрат
, греко-латинский квадрат 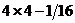 реплику от ПФЭ
реплику от ПФЭ 
 ,
,  реплику от ПФЭ
реплику от ПФЭ 
 .
.
 2017-12-16
2017-12-16 622
622








