Моменты инерции сечений простой формы

Теории прочности

В общем случае опасное напряженное состояние элемента конструкции зависит от соотношения между тремя главными напряжениями (s₁,s₂,s₃). Т.е., строго говоря, для каждого соотношения нужно экспериментально определять величину предельного напряжения, что нереально. Поэтому были приняты такие методы расчета прочности, которые позволяли бы оценить степень опасности любого напряженного состояния по напряжению растяжения – сжатия. Они называются теориями прочности (теории предельных напряженных состояний).

1-ая теория прочности (теория наибольших нормальных напряжений): причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. s_max= s₁£ [s]. Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.

2-ая теория прочности (теория наибольших относительных деформаций): причиной наступления предельного напряженного состояния являются наибольшие удлинения. e_max= e₁£ [e]. Учитывая, что e₁= , m — коэффициент Пуассона, получаем условие прочности s_эквII= s₁ — m(s₂ + s₃)£ [s]. s_экв — эквивалентное (расчетное) напряжение. В настоящее время теория используется редко, только для хрупких материалов (бетон, камень).

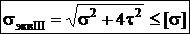3-я теория прочности (теория наибольших касательных напряжений): причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения t_max £ [t], t_max= , условие прочности: s_эквIII= s₁ — s₃£ [s]. Основной недостаток – не учитывает влияние s₂. При плоском напряженном состоянии: s_эквIII= £ [s]. При s_y=0 получаем Широко используется для пластичных материалов.

4-я теория прочности (энергетическая теория): причиной наступления предельного напряженного состояния являются величина удельной потенциальной энергии изменения формы. u_ф£[u_ф]. .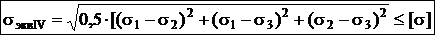

Учитывает, все три главных напряжения. При плоском напряженном состоянии: . При s_y=0,

Широко используется для пластичных материалов.

Теория прочности Мора Получена на основе кругов напряжений Мора. . Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [s_p] и сжатие [s_с] не одинаковы (чугун).

Для пластичных материалов [s_p]=[s_с] теория Мора превращается в 3-ю теорию.

 

Чистый сдвиг

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s₁= — s₃ = t; s₂= 0. Главные площадки составляют с площадками чистого сдвига угол 45^о.

При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,

g» — относительный сдвиг или угол сдвига.

Закон Гука при сдвиге: g = t/G или t = G×g.

G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).

Потенциальная энергия при сдвиге: .

Удельная потенциальная энергия деформации при сдвиге: ,

где V=а×F — объем элемента. Учитывая закон Гука, .

Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.

Круг Мора при чистом сдвиге.

Геометрические характеристики плоских сечений

Площадь: , dF — элементарная площадка.

Статический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние "y" от оси 0x: dS_x = y×dF

Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и x: ; 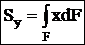[см³, м³, т.д.].

Координаты центра тяжести: . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями F_i и координатами центров тяжести x_i, y_i.Статический момент площади всей фигуры = сумме статических моментов каждой ее части: .

Координаты центра тяжести сложной фигуры:

Моменты инерции сечения

Осевой (экваториальный) момент инерции сечения — сумма произведений элементарных площадок dF на квадраты их расстояний до оси.

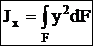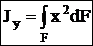; [см⁴, м⁴, т.д.].

Полярный момент инерции сечения относительно некоторой точки (полюса) — сумма произведений элементарных площадок на квадраты их расстояний от этой точки. ; [см⁴, м⁴, т.д.]. J_y + J_x = J_p.

Центробежный момент инерции сечения — сумма произведений элементарных площадок на их расстояния от двух взаимно перпендикулярных осей. .

Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с осями симметрии, равен нулю.

Осевые и полярные моменты инерции всегда положительны, центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.

Момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

 

Моменты инерции сечений простой формы

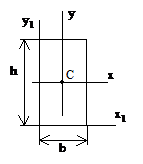
Прямоугольное сечение Круг

Кольцо

Треугольник

равнобедренный

Прямоугольный

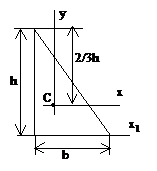треугольник

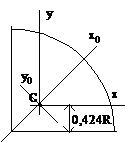Четверть круга

J_y=J_x=0,055R⁴

J_xy=±0,0165R⁴

на рис. (—)

J_x0=0,0714R⁴

J_y0=0,0384R⁴

 

Полукруг

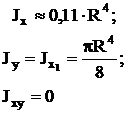
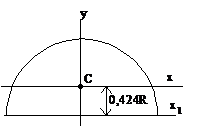Моменты инерции стандартных профилей находятся из таблиц сортамента:

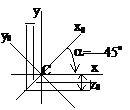
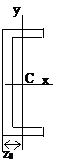
ДвутаврШвеллерУголок

 

Моменты инерции относительно параллельных осей:

J_x1=J_x + a²F;

J_y1=J_y + b²F;

 

момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. J_y1x1=J_yx + abF; ("a" и "b" подставляют в формулу с учетом их знака).

 

Зависимость между моментами инерции при повороте осей:

J_x1=J_xcos²a + J_ysin²a — J_xysin2a; J_y1=J_ycos²a + J_xsin²a + J_xysin2a;

J_x1y1= (J_x — J_y)sin2a + J_xycos2a;

Угол a>0, если переход от старой системы координат к новой происходит против час.стр. J_y1 + J_x1= J_y + J_x

Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если a₀>0 Þ оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:

J_max + J_min= J_x + J_y. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:

J_x1=J_maxcos²a + J_minsin²a; J_y1=J_maxcos²a + J_minsin²a; J_x1y1= (J_max — J_min)sin2a;

Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных центральных осей инерции. Радиус инерции — ; J_x=F×i_x², J_y=F×i_y².

Если J_x и J_y главные моменты инерции, то i_x и i_y — главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции i_x1 для любой оси х₁. Для этого надо провести касательную к эллипсу, параллельную оси х₁, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х₁: . Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, J_xy=0, эллипс инерции обращается в круг инерции.

 

Моменты сопротивления.

Осевой момент сопротивления — отношение момента инерции относительно оси к расстоянию от нее до наиболее удаленной точки сечения. [см³, м³]

Особенно важны моменты сопротивления относительно главных центральных осей:

прямоугольник: ; круг: W_x=W_y= ,

трубчатое сечение (кольцо): W_x=W_y= 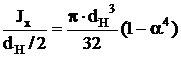, где a= d_Н/d_B.

Полярный момент сопротивления — отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения: .

Для круга W_р= .

Кручение

Такой вид деформации, при котором в поперечных сечениях возникает только одни крутящие моменты — М_к. Знак крутящего момента М_к удобно определять по направлению внешнего момента. Если при взгляде со стороны сечения внешний момент направлен против час.стр., то М_к>0 (встречается и обратное правило). При кручении происходит поворот одного сечения относительно другого на угол закручивания -j. При кручении круглого бруса (вала) возникает напряженное состояние чистого сдвига (нормальные напряжения отсутствуют), возникают только касательные напряжения. Принимается, что сечения плоские до закручивания остаются плоскими и после закручивания — закон плоских сечений. Касательные напряжения в точках сечения изменяются пропорционально расстоянию точек от оси. Из закона Гука при сдвиге: t=gG, G — модуль сдвига, , 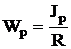— полярный момент сопротивления круглого сечения. Касательные напряжения в центре равны нулю, чем дальше от центра, тем они больше. Угол закручивания , GJ_p — жесткость сечения при кручении. 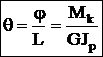— относительный угол закручивания. Потенциальная энергия при кручении: . Условие прочности: , [t] = , для пластичного материала за t_пред принимается предел текучести при сдвиге t_т, для хрупкого материала – t_в – предел прочности, [n] – коэффициент запаса прочности. Условие жесткости при кручении: q_max£[q] – допустимый угол закручивания.