Геометрические характеристики поперечных сечений бруса

1 2 3 4 5 6 7

Контрольные вопросы

1.Чем занимается наука о сопротивлении материалов?

2.Что такое прочность, жёсткость и устойчивость элементов конструкций?

3. Что понимается под расчётной схемой?

4. Какие силы называются внешними? Какие внутренними?

5. Для чего используется в сопротивлении материалов метод сечений? В чём он

заключается?

6. Количество внутренних усилий в поперечном сечении бруса, как они определяются?

7. Что такое напряжение? Какова его размерность?

8. Какие простые деформации может испытывать брус при его нагружении внешними силами?

2.1 Основные определения

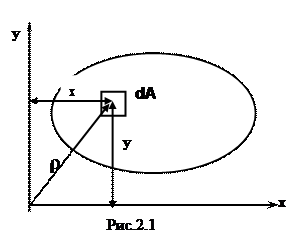При решении задач сопротивления материалов возникает необходимость оперировать определенными геометрическими характерис-тиками поперечных сечений бруса. В силу своего узкого прикладного значения в общем курсе геометрии они не изучаются.

Рассмотрим некоторое поперечное сечение бруса площадью А в системе координат х,у (рис.2.1 ). Интегралы

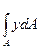S_х=и S_y=

называются статическими моментами площади поперечного сечения. Здесь dA – элементарная часть рассматриваемой площади (элементарная площадка) с координатами х,у. Размерность статического момента сечения [м³] или [см³]. Он может быть больше нуля, меньше нуля или равен нулю.

Если известны координаты центра тяжести сечения и его площадь, то статические моменты определятся по формулам

S_х= y_c А·, S_Y = x_с А,

из которых следуют выражения для определения координат центра тяжести

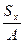y_с= , x_с= .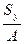

Интегралы

І_х =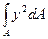, І_у =

называются осевыми моментами инерции сечения относительно соответственно осей х и у

Интеграл

І_ху =

называется центробежным моментом инерции сечения относительно осей х, у

Интеграл

І_ρ =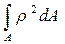

называется полярным моментом инерции сечения.

Размерность рассмотренных моментов инерции [м⁴] или [см^4]].

Так как ρ²= у²+ х²,тоІ_ρ = 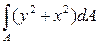= 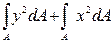,таким образом,

І_ρ= І_х+ І_у.

Осевые и полярный моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным или равным нулю.

Отношение осевого момента инерции к ординате наиболее удаленной от оси точки называется моментом сопротивления при изгибе: 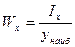-момент сопротивления при изгибе относительно оси х, 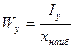- момент сопротивления при изгибе относительно оси у.

Отношение полярного момента инерции к радиусу наиболее удаленной точки от начала координат 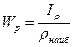называется полярным моментом сопротивления или моментом сопротивления при кручении.