 Пусть задана система координат главных центральных осей x0,y0, для которой известны моменты инерции
Пусть задана система координат главных центральных осей x0,y0, для которой известны моменты инерции 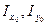 , центробежный момент инерции в этих осях равен нулю (рис.2.9). Вычислим моменты инерции этого сечения относительно новых осей x,y, повернутых по отношению к главным на угол α - угол между осямиx0 и x.Он будет положительным, если поворот от оси x0 к оси x происходит против часовой стрелки и отрицательным - если по часовой стрелке.
, центробежный момент инерции в этих осях равен нулю (рис.2.9). Вычислим моменты инерции этого сечения относительно новых осей x,y, повернутых по отношению к главным на угол α - угол между осямиx0 и x.Он будет положительным, если поворот от оси x0 к оси x происходит против часовой стрелки и отрицательным - если по часовой стрелке.
Из рис. 2.9 следует:
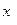 =
=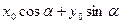 ,
,
y = 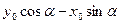
С учетом этих формул запишем выражения для моментов инерции рассматриваемого сечения в координатных осях x, y:
Iх =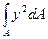 =
=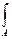 (у0 cоsα - х0 sinα)2dA =
(у0 cоsα - х0 sinα)2dA =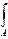 у
у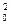 cоs2 α dA –
cоs2 α dA –
-2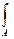 х 0у0cоsα· sinαdA+
х 0у0cоsα· sinαdA+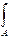
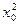 sin 2αdA,
sin 2αdA,
т.е. 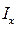 =
= 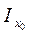 cоs 2α - 2 Іх 0у0cоsα·sinα +
cоs 2α - 2 Іх 0у0cоsα·sinα + 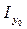 sin 2α.
sin 2α.
Іу = 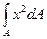 =
=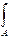 (х0csα + у0sinα)2dA =
(х0csα + у0sinα)2dA =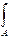 х
х cоs 2αdA ++2
cоs 2αdA ++2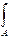 х 0 у0cоsα· sinαdA+
х 0 у0cоsα· sinαdA+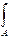 у
у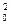 sin
sin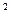 α dA=
α dA=
= 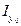 cоs 2α + 2 Іх 0у0cоsα · sinα +
cоs 2α + 2 Іх 0у0cоsα · sinα +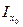 sin 2α.
sin 2α.
Іху= 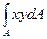 =
= 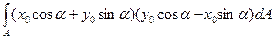 =
=
=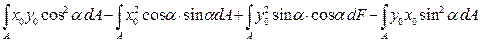 =
=
= 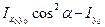 cos2α ·cоsα ·sinα +
cos2α ·cоsα ·sinα +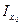 cоsα∙ sinα -
cоsα∙ sinα - 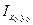 sin2α.
sin2α.
Так как 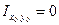 , cоsα ∙sinα =
, cоsα ∙sinα =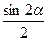 , то окончательно получим
, то окончательно получим
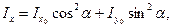
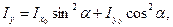
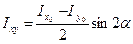 .
.
Складывая выражения Іх и Іу, получим
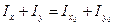 .
.
Таким образом, при повороте координатных осей сумма осевых моментов инерции не изменяется.
 2014-02-02
2014-02-02 1516
1516
