Использование коэффициента текущей ликвидности (КТЛ) для объективной оценки риска

Оценка риска с помощью леммы Маркова. Лемма Маркова гласит:
если случайная величина X не принимает отрицательных значений, то для любого положительного числа a справедливо следующее неравенство:

,

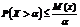где М (х) – математическое ожидание, т.е. среднее значение случайной.
величины; X – любая случайная величина.

Пример 1. Покупатель просит поставщика отпустить продукцию без предоплаты, т.е. в долг. Чему равна вероятность того, что поставщик получит оплату отпущенной продукции вовремя и не понесет потерь, если известно, что продолжительное время КТЛ покупателя находился на среднем уровне, равном 1.8? На какую минимальную прибыль должен рассчитывать поставщик, чтобы признать сделку целесообразной?

Решение:

При той информации, что здесь имеется, для оценки вероятности возврата долга можно использовать лишь лемму Маркова либо попытаться оценить упомянутую вероятность чисто субъективно. Первый вариант на вопрос о вероятности возврата долга дает такой ответ:

,

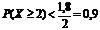т.е. вероятность возврата долга менее 90%, а потерь как минимум 10%. При таком риске потерь следует заключать сделку только в том случае, если она принесет прибыль более

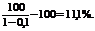
Последнее равенство получено из следующих соображений. Пусть долг выдан в размере Р. Тогда математическое ожидание величины возврата долга равно 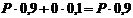, т.е. меньше выданной суммы. Чтобы матожидание возвращенной суммы хотя бы равнялось Р, нужно выдать долг под некоторый процент х. Тогда приравнивая матожидание возвращенной суммы выданной сумме Р получаем уравнение

.

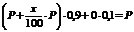Откуда получаем, что

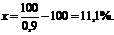
В качестве величины а здесь был взят тот порог, который отделяет платежеспособные предприятия от неплатежеспособных и которым согласно постановлению Правительства РФ от 20 мая 1994 г. № 498 «О некоторых мерах по реализации законодательства о несостоятельности предприятий» является КТЛ > 2. Значит, чтобы отдать долги поставщику, покупатель должен будет повысить значение КТЛ до 2.

Лемма Маркова может быть использована и тогда, когда математическое ожидание имеет вид не обычной средней величины, а ее доли. Пример такого использования леммы Маркова приводится ниже.

Оценка риска с помощью неравенства Чебышева. Неравенство Чебышева имеет такой вид:

.

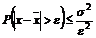Оно позволяет находить верхнюю границу вероятности того, что случайная величина X отклонится в обе стороны от своего среднего значения на величину больше .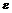

Эта вероятность равна или меньше (как максимум равна, не больше), чем

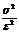, где 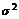- дисперсия СВ X, исчисляемая по формуле:

.

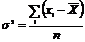Если нас интересует вероятность отклонения только в одну сторону, например, в большую, то вышеприведенное неравенство Чебышева надо было бы записать так:

.

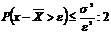Пример 2. У банка имеются два должника, значения КТЛ у которых за три прошедших месяца составили: у первого -1.5, 1.3 и 1.7 и у второго - 1.6, 1.4 и 1.5. Какова вероятность того, что они в течение ближайшего месяца погасят свои долги перед банком?

Решение:

Среднее значение КТЛ у обоих должников равно одной и той же величине: 1.5. В силу этого лемма Маркова здесь показала бы совершенно одинаковую вероятность погашения долга у двух должников:

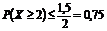, т.е. менее 75 %.

Вероятность же невозврата долга у обоих но лемме Маркова здесь со­ставила бы как минимум 25%.

Неравенство же Чебышева даст разные значения этих вероятностей для упомянутых должников, ибо оно кроме среднего уровня КТЛ учитывает еще и его колеблемость, которая у первого больше, чем у второго, что видно по величине дисперсий:

,

.

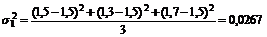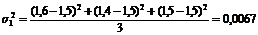Упомянутые должники погасят свой долг перед банком, если восстановят свою платежеспособность, т.е. повысят свой КТЛ до уровня 2. Для этого он у них должен будет отклониться в большую сторону от нынешнего своего значения как минимум на 0.5.

Вероятность такого отклонения в обе стороны по неравенству Чебышева равна:

для первого должника - ;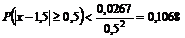

для второго - .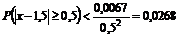

Нам, как уже отмечалось, нужна вероятность отклонения только в одну – большую сторону. Она составит для первого должника меньше
10.68% / 2 = 5.34%; для второго должника меньше 2.68%: 2=1.34%.

Таким образом, вероятность невозврата долга первым должником будет как минимум 100-5.34 = 94.66%, а вторым - как минимум 100 - 1.34 = = 98.66%.

Почему должник с меньшей колеблемостью показателей вернет ссуду с меньшей вероятностью? Ведь чем ниже колеблемость, тем выше, казалось бы, должна быть его надежность! Объясняется это очень просто. В данном примере меньшая колеблемость КТЛ у второго должника говорит о его большей устойчивости в состоянии неплатежеспособности. Быть устойчивым неплательщиком – отнюдь не положительное качество. Поэтому и вероятность невозврата им долга оказалась выше. Если бы у него была меньшая колеблемость вблизи значения КТЛ, равного, например, 2.5, тогда все обстояло бы у него по-другому. Но он «застрял» на КТЛ куда меньше 2.

Большим достоинством леммы Маркова и неравенства Чебышева является то, что они пригодны для употребления при любом количестве наблюдений и любом законе распределения вероятностей.

Платой за отсутствие жестких ограничений является некоторая неопределенность оценок уровня вероятности, причем при использовании леммы Маркова она значительно больше, чем при применении неравенства Чебышева.

Неопределенность оценок существенно снижается, если можно допустить наличие закона нормального распределения. Как известно, условия существования этого закона довольно широки, что позволяет допускать его наличие в очень многих случаях. Тогда при числе наблюдений, равном или более 30, для оценки вероятности того, что некая случайная величина X превысит заданный предел, можно воспользоваться выражением .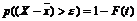

При числе наблюдений меньше 30, когда закон нормального распределения реализуется с известными отклонениями, расчет может быть выполнен по формуле: 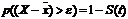, где F (t) – нормированная функция нормального распределения, S (t) – функция распределения Стьюдента.

Обе упомянутые функции табулированы. Их значения находятся по таблицам, входом в которые является величина t, определяемая как ,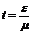

где m - стандартная ошибка.

Стандартная ошибка при числе наблюдений больше 30 находится по формуле:

.

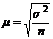При меньшем числе наблюдений

.

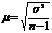В рассматриваемом примере КТЛ у первого должника принимал значения 1.5, 1.3 и 1.7, а дисперсия оказалась равной 0.0267. Стандартная ошибка для этого случая составит:

.

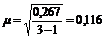Отсюда

.

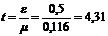По таблицам функции распределения Стьюдента S₂(4.31) = 0.975.

Здесь 2 = n –1 = 3 – 1 – число степеней свободы в распределении Стьюдента.

Следовательно, вероятность восстановления платежеспособности составит 1-0.975 = 0.025 или «точно 2.5%» вместо «не больше 5.34%» но неравенству Чебышева и «не более 75%» по лемме Маркова.

Ответы «точно 2.5%», «не больше 5.34%» и «не больше 75%», хотя и различаются между собой, однако по смыслу не противоречат друг другу. Они просто имеют разную меру неопределенности.

Использование модели равномерного распределения. Если предположить, что риск невозврата долга равномерно уменьшается с ростом значений КТЛ у заемщика, то для расчета вероятности невозврата им долга можно воспользоваться такой формулой:

.

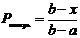Здесь b – верхняя граница зоны риска, а – нижняя граница зоны риска, х – фактическое значение КТЛ.

Приведем пример использования данной формулы.

Пример 3. Фирме предстоит заключение сделки с предприятием о поставке ему продукции на крупную сумму. Согласно бухгалтерским данным, фактическое значение КТЛ у этого предприятия равно 1.6.

Фирма ведет статистику неплатежей. Согласно ей, у контрагентов фирмы, оказавшихся должниками, КТЛ находился в интервале 1.2 - 1.8.

Чему равна вероятность того, что предприятие окажется неплатежеспособным и не сможет расплатиться за поставленную ему продукцию?

Решение:

Согласно приведенным выше данным, зону неопределенности или риска для значений КТЛ у контрагентов данного конкретного предприятия можно определить как 1.2 - 1.8. Отсюда вероятность невозврата долга за поставленную продукцию можно определить так:

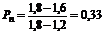, т.е. 33%.

На сделку с таким риском потерь можно идти только в том случае, если ожидаемая прибыль превысит:

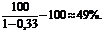
Если бы у предприятия не было собственной статистики неплатежей, то расчет уровня риска потерь здесь выглядел бы так:

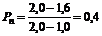, т.е. 40%.

Допущение о существовании закона равномерного распределения вероятностей банкротств является, конечно, в определенной мере натяжкой. Но когда нет точных данных о действительно существующем законе распределения вероятностей, то, естественно, приходится идти на подобные допущения. К тому же равномерный закон распределения вероятностей оказывается очень простым и легким к употреблению, а для использования других законов могут понадобиться основательные знания в области математики.

Противоположным понятию риска потерь выступает понятие надежности. Вероятность того, что партнер окажется надежным и не подведет, можно определить как:

.

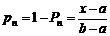При 33%-ном риске потерь надежность партнера будет равна 100% -33% = 67%.

Приведенные выше формулы можно использовать для перевода значений не только КТЛ, но и многих других показателей в вероятностные оценки риска. В частности, их можно применять для перевода баллов надежности банков, исчисляемых но методике В. Кромонова, являющейся сейчас одной из лучших. Рейтинги банков с ее использованием регулярно публикуются. По этим публикациям мы, например, установили что среди банков, у которых ЦБ РФ в то или иное время отозвал лицензию на право осуществления банковской деятельности, не было ни одного, который бы перешагнул границу в 60 баллов. В то же. время ни один банк из числа сохранивших лицензию не опускался ниже 30 баллов. Учитывая это, мы подсчитали вероятности отзыва лицензии у банков, находившихся в зоне неопределенности, т.е. имеющих баллы надежности по В. Кромонову в интервале 30 – 60.

Например, входивший в первую сотню крупнейших российских банков Тверьуниверсалбанк имел на 1 января 1996 г. 37.4 балла, исчисленных по методике В. Кромонова. По своим масштабам он считался очень надежным. Ведь лопаются чаще мелкие банки. Но наш расчет показал следующую вероятность краха этого банка:

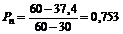, т.е. более 75%.

И действительно, в июле 1996г. ЦБ РФ отобрал у Тверьуниверсалбанка лицензию.

Оценка уровня риска с помощью выборки. Определить уровень риска можно и с помощью выборочного наблюдения за частотой появления тех или иных событий, которые ведут к потерям. Поскольку при этом данные, относящиеся к прошлому периоду, приходится распространять на будущее, постольку любые, самые обширные собранные сведения о частоте появления событий следует рассматривать как некую выборку из бесконечной совокупности со всеми вытекающими отсюда последствиями. А они сводятся к тому, что надо обязательно рассчитывать ошибки выборки.

Как известно, последние для доли исчисляются по формуле:

,

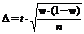где 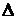– предельная ошибка выборки,

t – кратность ошибки, связывающая размер ошибки с заданной вероятностью,

w – выборочная доля или частость наступления события в эксперименте,

n – объем выборки.

Приведенная формула дает верные результаты, если величина w не слишком мала. При очень малых значения w, т.е. для очень редких событий, этой формулой пользоваться нельзя. Надо переходить на применение формулы вида:

.

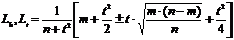Здесь L _h, L _t – верхний и нижний пределы генеральной доли (вероятности появления события),

n – объем выборки (число наблюдений),

m – число появлений события,

t – кратность ошибки.

Рассмотрим на следующем примере применение этих формул для оценки вероятности риска.

По статистике коммерческого банка «Восток» из 100 ссуд, выданных первоклассным заемщикам (группа А), по которым для расчета резервов на покрытие потерь от непогашения кредитов установлен коэффициент риска на уровне 2%, только одну ссуду, т.е. 1%, пришлось списать как безнадежную. Из 200 ссуд, выданных заемщикам, допустившим просрочки погашения ссуд до 30 дней (группа Б), по которым коэффициент риска установлен на уровне 5%, таких ссуд оказалось 10, т.е. 5% от числа выданных ссуд.

Даже если это абсолютно полные данные за прошлый период времени, то при попытке распространить их на предстоящее время они как бы превращаются в выборку из бесконечно большой совокупности и потому содержат ошибку репрезентативности. Ее обязательно надо учесть, если по этим данным надо будет принимать решения, касающиеся будущего. Нельзя считать, что в будущем по заемщикам группы А невозврат ссуд так иостанется на уровне 1%, а в группе Б - на уровне 5%. Он может оказаться в каком-то интервале, т.е. выше либо ниже В или 5%. Для банка главное –чтобы он не оказался выше. Ориентируясь на принятие решений в будущем, рассчитаем верхнюю границу упомянутого интервала.

Этот расчет для ссуд, выданных заемщикам группы Б, следует сделать так:

а) определить предельную ошибку выборки, имеющую 90%-ную вероятность по первой формуле:

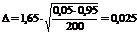, или 2,5%.

Здесь величина 1.65 – квантиль нормального распределения для 90%-ного доверительного интервала.

б) найти верхнюю границу заданного интервала

w + D =5%+2.5% = 7.5%.

Для ссуд, выданных заемщикам группы А, где невозврат ссуд является очень редким событием, для расчета верхней границы заданного интервала надо прибегнуть к помощи второй формулы:

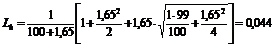, т.е. 4,4%.

Проделанные расчеты говорят о том, что реальная вероятность невозврата ссуд в двух вышеупомянутых группах заемщиков может превысить установленные коэффициенты риска, в результате чего созданного на их основе резерва для погашения потерь по ссудам может не хватить на полное возмещение убытков банка из-за невозврата ссуд.

Так, в группе А вероятность невозврата ссуд может достигнуть 4,4%, а в группе Б – 7.5% и даже оказаться выше этих пределов, но это маловероятно. Вероятность такого превышения составляет (100% - 90%): 2 = 5%.

Риск невозврата ссуд нельзя занижать, ибо это грозит банку прямыми убытками. Чтобы этого не произошло, при обработке статистических данных о невозвратах ссуд надо правильно пользоваться вышеприведенными формулами. Надо помнить, что при обработке информации о редких событиях следует применять только вторую формулу. Первая в таких условиях может существенно занизить уровень риска. Например, если известно, что из 100 выданных ссуд не было ни одной непогашенной, т.е. доля невозврата ссуд оказалась равной нулю, то не следует думать, что и в будущем этот показатель будет равен нулю, как это получится, если пользоваться первой формулой. Верхняя граница 90% -ного доверительного интервала, исчисленная с помощью второй формулы, здесь составит:

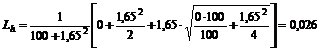, т.е. 2,6%.

Если при решении каких-то деловых проблем в прошлом только в одном случае из 10 произошел сбой, то не следует рассчитывать на 10%-ную вероятность сбоев в будущем. 90%-ный доверительный интервал вероятности сбоев в таком случае составит:

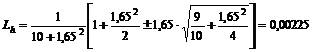, 0,3486.

Другими словами, вероятность сбоев здесь может быть в пределах 0,2% – 35%. К тому, что она может оказаться значительно меньше 10%, можно отнестись без особого внимания. Игнорировать же возможность появления сбоев на уровне 35% очень опасно, поскольку это может привести к серьезным потерям. Чтобы избежать их, надо с особой тщательностью подходить к определению верхнего предела доверительного интервала, используя для этого правильную схему расчета.

Надо хорошо помнить, что применять первую из приведенных выше формул для определения предельной ошибки, а затем и границ доверительного интервала можно только при достаточно большом числе наблюдений и для событий, которые нельзя назвать редкими. Если бы мы воспользовались ею в нашем последнем примере, то получили бы верхний предел доверительного интервала на уровне только 26%, что давала бы довольно заниженное представление о действительном уровне риска.