2017-12-16
2715
Применение в анализе рядов динамики методов укрупнения интервалов, скользящей средней, экспоненциального сглаживания позволяет выявить тренд для его описания, но получить обобщенную статистическую оценку тренда посредством этих методов не возможно. Решение этой более высокого порядка задачи достигается методом аналитического выравнивания.
Метод аналитического выравнивания. Он позволяет получить обобщенную статистическую оценку тренда. Тренд yt рассчитывается как функция времени.
. (22)
Определение теоретических (расчетных) уровней 
производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития ряда динамики.
Подбор математической функции осуществляется методом наименьших квадратов
. (23)
Таким образом, сумма отклонений между теоретическими и эмпирическими (полученными на практике) уровнями 
должна быть минимальна.
Формула (8.23) – это критерий соответствия расчетных и фактических уровней РД.
Главное здесь – подбор математической функции.
Различают следующие эталонные типы развития явлений во времени:
а) равномерное развитие – если абсолютные приросты в РД постоянны:
∆уц ≈ const.
Основная тенденция развития в РД со стабильными абсолютными приростами отображается уравнением прямолинейной функции (линейный тренд):
(24)
Здесь а0, а1 - параметры уравнения; t - обозначение времени.
Параметр а1 является коэффициентом регрессии, определяющим направление развития. Если а1 > 0, то уровни РД равномерно возрастают, при а1 < 0 происходит равномерное снижение уровней РД.
б) равноускоренное (равнозамедленное) развитие – уровни таких РД изменяются с постоянными темпами прироста:
Tпцi ≈ const
Основная тенденция развития в РД со стабильными темпами прироста отображается функцией параболы второго порядка (квадратичный тренд):
(25)
Здесь значения параметров а0, а1 идентичны параметрам линейного тренда,
а2 - параметр, характеризующий изменение интенсивности развития в единицу времени (ускорение развития или процесс замедления роста).
в) развитие с переменным ускорением (замедлением) – парабола третьего порядка:
(26)
а3 - параметр, отображающий изменение ускорения.
г) развитие по экспоненте – для стабильных темпов роста. Математически это показательная функция:
(27)
д) развитие с замедлением роста в конце периода (показание абсолютного прироста сокращается в конечных уровнях ряда динамики). Математически это полулогарифмическая функция:
(28)
При изучении неудовлетворенного и реализованного спроса применяют:
е) степенную функцию:
(29)
ж) функцию гиперболы:
(30)
На практике выбор эталонной математической функции достаточно сложная и трудоемкая операция (даже при использовании соответствующего программного обеспечения). Особенно это имеет место для криволинейных функций, теория которых разработана недостаточно.
Для вычисления параметров функции линейного тренда на основе метода наименьших квадратов составляется система нормальных уравнений:
(31)
Для решения системы применяется способ определителей, позволяющий получать более точные результаты за счет сведения к минимуму ошибки из-за округлений в расчетах параметров:
(32)
Здесь значения времени – это целые числа (коды).
Для упрощения расчетов используется специальный подбор показателей времени так, чтобы их сумма равнялась нулю (способ расчета времени от условного начала):
Например, если число уровней в РД нечетное и равно 7, условные значения показателей времени равны:
-7 -5 -3 -1 0 1 3 5 7
Тогда расчет коэффициентов линейного тренда значительно упрощается и м.б. выполнен по формулам:
(33)
После определения параметров линейного тренда подставляем их в искомое линейное уравнение и находим теоретические (выровненные) значения .
Одним из наиболее часто применяемых показателей адекватности математической функции (математической модели) является стандартизованная ошибка аппроксимации:
(34)
Она должна быть минимальна у выбранной теоретической модели тренда.
Практическое использование: Компания Wm. Wrigley Jr. Company имеет штаб-квартиру в г.Чикаго. Эта компания является крупнейшим производителем жевательной резинки в США, управляет 12 фабриками и продает свою продукцию в более чем 100 странах. Рыночная стоимость компании составляет 13 млрд.долл.
Фактические доходы компании приведены в табл. и на рис. Затем с помощью индекса потребительских цен (Consumer Price Index – CPI), вычисляемого Бюро статистики Министерства труда США фактические доходы были преобразованы в реальные. Для этого величина фактического дохода делится на CPI и умножается затем на 100. Значения и график реального дохода в ценах 1982г. приведены в табл. и на рис.
| Год | Код | Фактический доход | CPI-U | Реальный доход |
| 581,5 | 96,5 | 602,59 | ||
| 581,7 | 99,6 | 584,04 | ||
| 590,5 | 103,9 | 568,33 | ||
| 620,3 | 107,6 | 576,49 | ||
| 699,0 | 109,6 | 637,77 | ||
| 781,1 | 113,6 | 687,59 | ||
| 891,4 | 118,3 | 753,51 | ||
| 992,9 | 124,0 | 800,73 | ||
| 1110,6 | 130,7 | 849,73 | ||
| 1148,9 | 136,2 | 843,54 | ||
| 1301,3 | 140,3 | 927,51 | ||
| 1440,4 | 144,5 | 996,82 | ||
| 1661,3 | 148,2 | 1120,99 | ||
| 1769,7 | 152,4 | 1161,22 | ||
| 1850,6 | 156,9 | 1179,48 | ||
| 1954,2 | 160,5 | 1217,57 | ||
| 2023,4 | 163,0 | 1241,35 | ||
| 2079,2 | 166,6 | 1248,02 | ||
| 2145,7 | 172,2 | 1246,05 | ||
| 2429,6 | 177,1 | 1371,88 |
Значения переменной t (показатель времени) обозначим с помощью целых чисел от 0 до 19. Затем обработаем модифицированные значения показателя времени и реального дохода с помощью программы McExcel.
| Модель линейного тренда для реального годового дохода | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,984 | |||||
| R-квадрат | 0,968 | |||||
| Нормированный R-квадрат | 0,966 | |||||
| Стандартная ошибка | 50,205 | |||||
| Наблюдения | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 498,656 | 21,636 | 23,048 | 8,21605E-15 | 453,201 | 544,111 |
| Код | 45,485 | 1,947 | 23,363 | 6,48317E-15 | 41,394 | 49,575 |
Тогда уравнение линейного тренда (линейной регрессии) примет вид:
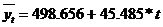
Регрессионные коэффициенты (параметры уравнения) интерпретируются следующим образом:
а0 =498,656 - среднее значение реальных доходов компании,
а1 - повышение реальных доходов кампании в среднем на 45,485 млрд. долл. в год.
Модель полученного линейного тренда реальных доходов компании представлена на рис.
Теоретические (расчетные) значения доходов можно определить, подставляя в полученное уравнение значения t в пределах от 0 до 19 с шагом 1.
Расхождения между теоретическими и практическими значениями доходов характеризуются среднеквадратической ошибкой аппроксимации.
Аналогичным образом строится модель квадратичного, экспоненциального и других видов тренда.
Применение понятий:
По данным о розничном товарообороте региона (см. табл.) синтезировать трендовую модель товарооборота.
Выполнение задания:
| Год | Объем розничного товарооборота, млрд.руб. | Темп роста по годам, % | Абсолютный прирост по годам, млрд.руб. |
|
По виду функции (см. рис.) наметим типы функций для анализа:
1) - прямолинейная,
2) - показательная функция,
3) - парабола второго порядка.
|
|
Используем способ отсчета времени от условного начала
n = 5;
тогда условные значения показателей времени представим в виде:
t = -2, -1, 0, 1, 2.
1) для прямолинейной функции:
| год |
2) для показательной функции
3) для параболы 2-го порядка:
Составим для определения параметров в уравнениях тренда вспомогательную таблицу:
| Год | Условные обозначения времени | yi | ti yi | ti2 yi | lg yi | ti lg yi | |||
| ti | ti2 | ti4 | |||||||
| -2 | 16.4 | -32.8 | 65.6 | 1.21484 | -2.43 | ||||
| -1 | 16.9 | -16.9 | 16.9 | 1.22789 | -1.23 | ||||
| 17.8 | 1.25042 | ||||||||
| 18.3 | 18.3 | 18.3 | 1.26245 | 1.26 | |||||
| 19.1 | 38.2 | 76.4 | 1.28103 | 2.56 | |||||
| å | 88.5 | 6.8 | 177.2 | 6.23663 | 0.17 |
1) Вычислим параметры для уравнения линейного тренда. Далее подставим найденные параметры в исходное уравнение и рассчитаем теоретические значения для каждого анализируемого года:
определим стандартизованную ошибку аппроксимации для прямолинейного тренда:
млрд.руб.
2) Вычислим параметры для уравнения показательной функции:
lg a0=6,24/5=1.25 или a0=17.67
lg a1=0.17/10=0.02 или a1=1.04
С использованием рассчитанных параметров составим уравнение трендовой модели для показательной функции: lg 
=1.25+t*0.02 или 
=17.67 * 1.04t
Определим для каждого года по синтезированной модели теоретические (расчетные) уровни. Для этого в теоретическое уравнение подставим условные значения показателей времени:
lg yt1=1.2/395=1.25+(-2)*0.02 => yt1 =16.37 млрд. руб. для 2000г.
lg yt2=1.23 => yt2 =17.01 млрд. руб. для 2001г.
lg yt3=1.24 => yt3 =17.67 млрд. руб. для 2002г. =>
=> lg yt4=1.26 => yt4 =18.36 млрд. руб. для 2003г.
lg yt5=1.28 => yt5 =19.09 млрд. руб. для 2004г.
Определим стандартизованную ошибку аппроксимации для показательного тренда:
млрд.руб.
3) Аналогичные расчеты выполним для уравнения параболы 2-го порядка. Вычислим параметры:
a0=17.67; a1=6.6/10=0.68; a2=0.014.
С использованием этих параметром синтезируем трендовую модель:
=> =17.67+ 0.68t+0.014t2
Подставляя в эту модель условные значения показателей времени определим теоретические значения уровней (млрд.руб):
=> yt1=16.37; yt2=17.0; yt3=17.67; yt4=18.36; yt5=19.1.
Определим стандартизованную ошибку аппроксимации для квадратичного тренда:
=> 
млрд.руб.
В результате сравнения полученных значений стандартизованной ошибки аппроксимации следует, что по критерию минимальности предпочтение для дальнейшего использования следует отдать трендовой модели =17.67 * 1.04t, синтезированной на основе показательной функции 
.
