2017-12-16
737
Теория экстремумов функции имеет многочисленные практические применения.
Пусть функция непрерывна на отрезке 
. Тогда на этом отрезке функция 
достигает наибольшего и наименьшего значений (на основании свойств непрерывных функции). Функция может достигать своего наименьшего или набольшего значения внутри отрезка, или на концах отрезка.
Правило отыскания наибольшего и наименьшего значений непрерывной на отрезке функции.
1) Найти все максимумы и минимумы функции на отрезке.
2)Найти значения функции на концах отрезка, т.е. 
.
3)Из всех полученных значений функции выбрать наибольшее и наименьшее
Пример. На отрезке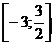 
найти наименьшее и наибольшее значение функции 
.
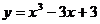1) 
.
.
2) 
1) Итак.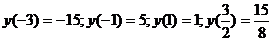 
- следовательно
.
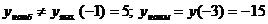Заключение.
Из самых различных областей науки и техники возникает большое количество практических задач, решение которых связано с исследованием функций и, в частности, с нахождением наибольших и наименьших значений. Вместе с тем рассматриваемые в лекции вопросы будут неоднократно встречаться и при дальнейшем изучении математического анализа.
Следует обратить особое внимание на практическую сторону вопроса, то есть на методику исследования функций, построения графиков и решения задач.
