Экстремум функции. Необходимое условие экстремума

Говорят, что функция у=f(х) имеет максимум (минимум) при , если для всех значений и достаточно близких к выполняется неравенство f(x)<f();(f(x)>f())

Точки кривой близки точки максимума расположены выше этой точки().

Максимум и минимум функции называются экстремумами, точка -точка экстремума.

Теорема 1. (Необходимое условие экстремума) Если функция, у=f(х) дифференцируема в промежутке (а, в), имеет в некоторой точке внутри этого промежутка экстремум, то её производная в этой точке равна нулю, т.е

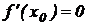(1)

Теорема позволяет установить отсутствие у функции экстремума, если производная исследуемой функции не имеет критических точек, т.е. действительных корней.

Условие (1) означает, что в точке экстремума дифференцируемой функции f(x) касательная параллельна оси Ох.

Функция может иметь экстремум и в точках, где производная не существует, например, графиком такой функции имеет узлом.

Значение аргумента при которых производная равна нулю или не существует, называются критическими.

Таким образом, если функция имеет экстремум, то он может быть только в критических точках.