Условия возрастания и убывания функции.

Исследование функции на экстремум.

1.Условия возрастания и убывания функции.

2. Экстремум функции. Необходимое условие экстремума.

3.Достаточные признаки существования экстремума.

 

Введение.

Основным содержанием данной лекции является исследование функции и построение графиков. Это важнейшие практические результаты математической теории. Аппарат дифференциального исчисления представляет возможность для создания более совершенных методов исследования функции. С помощью производных первого и второго порядка можно, оказывается, достаточно быстро и полно выяснить все наиболее характерные особенности в поведении той или иной функции.

 

Условия возрастания и убывания функции.

 

Функция y=f(x) называется возрастающей (убывающей) в промежутке

(а, в),если большему значению аргумента в этом промежутке соответствует большее (меньшее) значение функции.

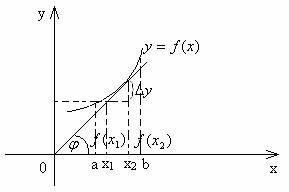
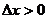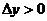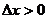Это значит, что для любых и в промежутке (а, в) в случае возрастания функции неравенству соответствует неравенство f()>f(),т.е. и ,а в случае убывания неравенство f ()>f(),т.е. и .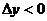

 

Теорема 1. (Необходимый признак возрастания (убывания) функции в данном промежутке)

Если функция y=f(x) дифференцируема в промежутке (а, в),то при всех значениях а<x<в её производная неотрицательна (неположительная).

Из графика возрастающей функции видно, что касательные к кривой наклонены к оси Ох под острым углом, а убывающей под тупым углом. Такое расположение касательных определяет неотрицательные (неположительные) значения угловых коэффициентов, что приводит к условию (), которое равносильно .

 

Теорема 2. (Достаточные признаки возрастания (убывания) функции в данном промежутке)

Если дифференцируемая в промежутке (а, в) функция y=f(x) имеет при любом значение а<x<в положительную (отрицательную) производную, то эта функция возрастает (убывает) в данном промежутке.

 

Для исследования функции на возрастание и убывание необходимо:

1. Найти область определения функции.

2. Найти её производную.

3. Найти значения х, при которых .

4. Разбить всю область существования функции найденными значениями х на отдельные промежутки и для каждого из них найти знак производной: если то на данном промежутке функция возрастает, если - функция убывает.

 

Пример. Исследовать на возрастание и убывание функцию y=2

1) Д(у)=R

2)

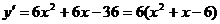
3)

x	(-∞; -3)	-3	(-3; 2)		(2; +∞)
yI	+		-		+
y

Возраст. Убывающ. Возраст.