2017-12-16
985
Из того факта,что 
, ещё не следует,что функция f(х) имеет экстремум при х= 
.
Из графика видно, что в точке х=0 экстремума нет, касательная пересекает кривую. Таким образом, не для всякого критического значения аргумента функция f(х) имеет место экстремум этой функции. Поэтому наряду с необходимым условием дадим достаточные условия экстремума в точке.
Теорема2. Пусть функция f(х) непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала, кроме, быть может самой точки .Если при переходе аргумента слева на право через точку производная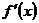 
меняет знак с + на -, то функция в этой точке имеет максимум; если знак меняется с – на +, то функция имеет минимум.
Замечание. Если для дифференцируемой функции 
её производная 
, но при переходе через это значение производная сохраняет постоянный знак, то при 
функция экстремума не имеет.
Правило1. Исследования функции на экстремум.
1) Найти область определения функции.
2) Найти производную функции 
.
|
|
|
3) Найти критические точки.
4) Установить знак производной вблизи критических точек и определить характер экстремума.
5) Вычислить значение функции в точках экстремума.
Пример. Исследовать на экстремум функцию 
1) 
.
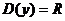2) 
3) 
- не существует при 
.
| x | (-∞;  )
|
| (; 1)
| (1; +∞ | |
| yI | + | - | + | ||
| y | ↑ | 
| ↓ | ↑ |
4)
max min
1
Достаточные условия существования экстремума можно проверить и с помощью второй производной, если исследуемая функция дифференцируема не менее двух раз.
Теорема3. Если для дифференцируемой функции в некоторой точке её первая производная , а вторая производная существует и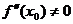 
, то, если 1) 
, то 
- минимум функции ; 2) если 
, то - максимум функции .
Правило2. Исследование функции на экстремум.
1) Найти 
2) Найти
3) Найти 
, при которых 
4) Найти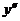 
5) Найти знак второй производной в критических точках.
Пример. Исследовать функцию 
на экстремум.
1)
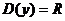
2) 
;
3) 
.
4) 
5) 
