Методы вариационного исчисления

Основная задача вариационного исчисления - исследование функционалов на экстремум и отыскание тех функций, на которых этот экстремум достигается.

Приведем примеры таких задач.

1 Из всех кривых на плоскости, соединяющих точки А и В, найти ту, которая имеет наименьшую длину. Ответ очевиден: отрезок прямой, соединяющей точки А и В.

2. Из различных дорог, соединяющих пункты А и В, выбрать ту, по которой стоимость проезда из А в Б минимальна.

Здесь ответ уже не столь очевиден. Прямолинейный путь из А в Бможет оказаться труднопроходимым и дорогим, а более длинный путь может оказаться более выгодным.

Большую роль в развитии вариационного исчисления сыграли следующие классические задачи.

1 Задача о брахистохроне - линии, по которой материальная точка быстрее всего соскальзывает под действием силы тяжести из точки А в точку В (А и В не лежат на одной вертикали) (Иоганн Бернулли).

2. Задача о геодезической линии — линии наименьшей длины, расположенной на заданной поверхности и соединяющей две данные точки (Якоб Бернулли).

3. Задача Дидоны — легендарной карфагенской царевны, которой понадобилось ремешком данной длины ограничить участок земли наибольшей площади (Леонард Эйлер).

Определение вариации. Рассмотрим функционал V[ y(x) ]. Зафиксируем функцию у₀(х) из области определения функционала V[y]. Тогда любую другую функцию у(х) из этой области можно представить в виде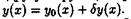

Изменение аргумента функционала V[y] — функцию δ· у(х) называют вариацией аргумента у₀(х).

Приращением функционала V[y] в точке у₀(х), отвечающим вариации аргумента δ· у(х), называется величина

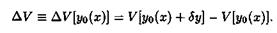
Выражение ΔV является функционалом от δ· у(х).

Дадим определение вариации функционала,удобное с технической точки зрения.

Если приращение функционала

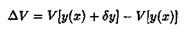
можно представить в виде

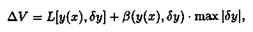
где L[y(x), δy] — линейный по отношению к δ у функционал, max / δ у / — максимальное значение \6у\ и β(y(x), δy)→ 0 при max / δ у / → 0, то линейная по отношению к δ у часть приращения функционала, т. е. L[y(x),δy], называется вариацией функционала и обозначается δ V.

Зафиксируем теперь аргумент у(х) функционала V[ у(х) ], зададим и тоже зафиксируем некоторую вариацию δ у аргумента у(х) и рассмотрим семейство кривых у(х, а) = у(х)+аδу, где а — произвольный параметр. На кривых у(х, а) функционал V[у] превращается в функцию V(a) параметра а.

Вариацией δ V функционала V[y] при у = у(х) называется производная при а = 0:

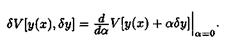
1°. Экстремум, функционала. Говорят, что функционал V[y] достигает локального минимума (максимума) на кривой у = 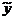(х) в рассматриваемом линейном нормированном пространстве Е (например, в С или в С¹), если в этом пространстве существует такая ε-окрестность кривой у = 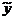(х), что для любой кривой у = у(х) из этой окрестности справедливо неравенство

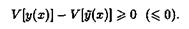
Кривые у = у(х) из ε -окрестности 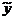называют кривыми сравнения.

В случае строгого неравенства говорят о строгом минимуме (максимуме). Если нет ограничений на размер ε-окрестности кривой 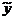в определении минимума (максимума), то говорят, что на кривой 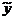достигается абсолютный минимум (максимум) функционала.

2°. Необходимое условие экстремума функционала. Пусть на кривой у = 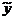(х) € Е достигается локальный экстремум функционала и пусть на 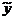существует вариация δ V[ 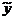,δy]. Тогда выполняется условие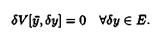

Простейшая задача вариационного исчисления. Рассмотрим функционал

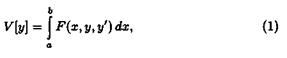
где 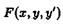— дважды непрерывно дифференцируемая функция.

Граничные точки допустимых кривых будем считать закреплен­ными: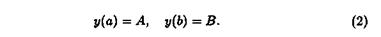

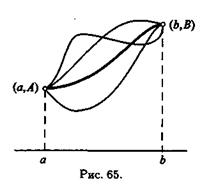
Простейшая задача вариационного исчисления ставится так: среди всех функций у(х), имеющих непрерывную производнуюи удовлетворяющих условиям (2), найти ту, которая доставляет экстремум функционалу (1). Эту задачу называют также задачей с закрепленными границами (рис. 65).

2°. Уравнение Эйлера. Усилим требования к гладкости кривых, на которых рассматривается функционал (1). Пусть кривая у = 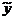(х) реализующая экстремум функционала (1), имеет вторую непрерывную производную. Для того, чтобы функционал (1), определенный на множестве кривых у(х) € С²[а,b], удовлетворяющих граничным условиям (2),

достигал экстремума на кривой у(х) G € С²[а,Ь], необходимо, чтобы эта кривая удовлетворяла уравнению Эйлера

Решения (интегральные кривые) уравнения Эйлера будем называть экстремалями (иногда экстремалью называют только у(х)).

Учитывая граничные условия (2), приходим к граничной задаче, которой должна удовлетворять функция у(х), доставляющая экстремум функционалу (1) с граничными условиями (2):

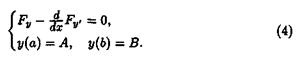
Уравнение Эйлера является при уравнением второго порядка, которое в развернутом виде выглядит так:

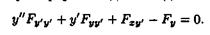
Как известно, краевая задача (4) для уравнения второго порядка может иметь единственное решение, может иметь множество решений, а может не иметь ни одного.

Решения задачи (4) аналогичны стационарным точкам в задаче исследования на экстремум функции одной или нескольких переменных. Дальнейшее исследование того, действительно ли на решениях задачи (4) достигается экстремум, проводится с использованием достаточных условий экстремума.