2017-10-31
828
ИССЛЕДОВАНИЕ ВРЕМЕННЫХ И ЧАСТОТНЫХ ХАРАКТЕРИСТИК ДЕТЕРМИНИРОВАННЫХ
СИГНАЛОВ
к лабораторной работе №1 по курсу
«Теория передачи сигналов»
САНКТ-ПЕТЕРБУРГ
Цель работы: углубление и закрепление знаний о связях между формами сигналов и их спектрами напряжений, о спектрах мощности и автокорреляционных функциях сигналов.
Содержание работы:
1) построение формы сигналов заданных аналитическим выражением u(t);
2) определение спектра напряжения сигнала 
при различном числе гармоник и построение графиков;
3) воспроизведение формы сигнала при ограниченном его спектре 
и оценка погрешности воспроизведения;
4) определение спектра мощности 
детерминированного сигнала по его спектру напряжения ;
5) определение функции автокорреляции 
по форме сигнала идеального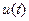 
и восстановленного при ограничении спектра .
Краткие теоретические сведения
Многообразие сигналов, применяемых в системах передачи информации, приводит к необходимости выявления и использования их закономерностей для решения задач обработки сигналов при передаче и приёме информации. В зависимости от имеющихся априорных данных сигналы разделяются на детерминированные и случайные. Детерминированными сигналами являются периодические и непериодические сигналы.
Для детерминированных сигналов существует аналитическое описание, полностью определяющее значения их характеристик во временной и частотной областях. К характеристикам во временной области относится форма сигнала u(t) и функция автокорреляции R(τ). В частотной области такими характеристиками являются спектральная плотность напряжения U(jω) и спектральная плотность мощности S(ω), далее – спектр напряжения и спектр мощности соответственно.
Взаимосвязь между характеристиками показана на рис.1 Направление стрелок отражает возможность перехода от одной характеристики к другой.
Рис. 1
Как видно из рис.1 форма сигнала u(t) и спектр напряжения U(jω), функция автокорреляции R(τ) и спектр мощности S(ω) образуют две взаимосвязанные пары. Внутри каждой пары переход от одной характеристики к другой осуществляется с помощью ряда Фурье для периодического сигнала или преобразования Фурье для непериодического сигнала.
Между характеристиками внутри каждой области (временной и частотной) существует также односторонняя связь: функция автокорреляции может быть определена по известной форме сигнала, а спектр мощности получен из спектра напряжения. Таким образом, форма сигнала и спектр напряжения являются базовыми характеристиками при описании детерминированных сигналов: зная любую из них можно определить остальные. Обычно известна форма сигнала 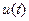, исходя из которой вычисляются другие характеристики.
Так, исследование сигнала в частотной области по его спектрам напряжения и мощности является задачей анализа, которая состоит в определении уровней частотных составляющих и количественных соотношений между ними с целью выявления более существенных из них. Для периодического сигнала анализ заключается в его разложении на ортогональные компоненты элементарной формы (например, гармонические: cos ωkt и sin ωkt), уровни которых в своей совокупности образуют спектр.
Восстановление сигнала (его формы) по спектральным компонентам является задачей синтеза. Обработка сигнала состоит в решении совокупности этих задач, либо одной из них.
Детерминированные сигналы используются в системах передачи дискретных сообщений, в которых нули и единицы передаются видеоимпульсами прямоугольной, косинусоидальной или другой формы, либо радиоимпульсами – гармоническими сигналами определённой частоты и длительности.
Знание временных и частотных характеристик таких сигналов позволяет осуществить рациональный выбор их формы (амплитуды, длительности); метода приёма; оценить взаимные влияния между сигналами; дальность передачи и помехоустойчивость.
Допустим сигнал задан аналитическим выражением:
Спектр напряжения сигнала определяется прямым преобразованием Фурье от u(t):
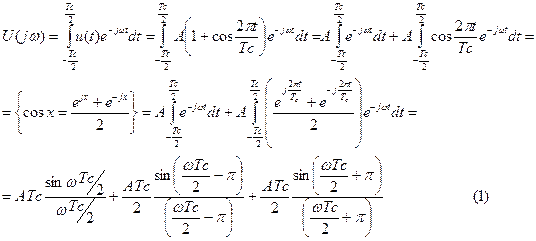
Огибающая спектра напряжения этого сигнала определяется суммой трёх слагаемых: огибающей спектра напряжения прямоугольного импульса, симметричной относительно оси ординат и максимумом равным АТс (первое слагаемое), и двух огибающих напряжения этого же импульса, сдвинутых относительно начала координат на π: влево (второе слагаемое) и вправо (третье слагаемое) и максимумами равными АТс/2, рис.2.
Рис. 2
Приведённая на рис.2 зависимость огибающей спектра напряжения сигнала от частоты содержит информацию об изменении амплитуд и фаз частотных составляющих спектра, который характеризуется следующими основными параметрами: монотонным (гладким) или немонотонным поведением; интенсивностью изменения амплитуд частотных составляющих; наличием точек перегиба; полярностью и видом фазовой характеристики.
Спектр мощности детерминированного сигнала связан со спектром напряжения соотношением:
В отличие от спектра напряжения он не содержит сведений о фазах частотных составляющих сигнала.
Функция автокорреляции детерминированного сигнала может быть определена через обратное преобразование Фурье его спектра мощности S(ω):
либо как интеграл свёртки:
,
который характеризует взаимозависимость (меру сходства) между значениями одного и того же сигнала, сдвинутых на время τ. При τ = 0 значение R(τ = 0) определяет энергию сигнала. Так как эта функция симметрична относительно τ = 0, её значения можно вычислять только при положительных (или отрицательных) значениях τ:
Вычисленная по этому значению функция автокорреляции для треугольного сигнала:
определяется выражением:
Энергия этого сигнала при τ = 0 равна 
.
Для расчётов R(τ) удобно пользоваться дискретным представлением сигнала, рис.3. В этом случае форма сигнала аппроксимируется импульсами шириной ∆t.
Рис. 3
В каждом импульсе записывается его амплитуда, соответствующая значению m. Тогда значения дискретной функции автокорреляции вычисляются при последовательном сдвиге копии сигнала относительно самого сигнала шагами m∆τ = ∆t·m:
,
где ∆τ = ∆t; 
; 
- для четных значений 
;
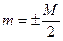- для нечетных значений .
Для каждого значения сдвига на m шагов составляются расчётные выражения вида:
,
,
и т.д.
