Теоретическое введение. Магнитное поле порождается движущимися электрическими зарядами

 

Магнитное поле порождается движущимися электрическими зарядами. Движущиеся заряды (токи) изменяют свойства окружающего их пространства – создают магнитное поле. Обнаружить магнитное поле можно тоже только с помощью проводника с электрическим током. Выражение для силы 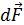, действующей на элемент тока 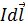в магнитном поле с индукцией 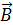, было получено экспериментально Ампером и носит название закона Ампера:

,

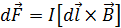или в скалярном виде

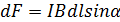(1),

где α – угол между вектором магнитной индукции 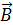и направлением тока в элементе .

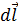Рассмотрим поведение контура с током в однородном магнитном поле. Магнитное поле однородно, если в каждой точке поля величина и направление вектора 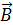одни и те же ( 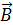=const).

Пусть силовые магнитные линии (линии вектора 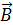) перпендикулярны плоскости рис.1. и выходят на нас, а плоскость прямоугольной рамки с током совпадает с плоскостью рисунка.

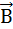
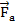
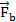
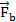
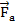
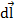
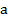
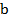
Рис.1

 

Обозначим стороны рамки через a и b, а направление тока – по часовой стрелке. Выберем бесконечно малый элемент 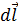с током I. На этот элемент со стороны магнитного поля действует сила

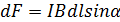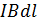= , (2)

т.к. α=90⁰. Интегрируя (2) по длине стороны a, получим 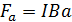(3). Направление этой силы, определяемое с помощью правила левой руки, показано на рис.1. Такая же сила 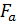действует и на противоположную сторону рамки a.

Аналогично запишем силы, действующую на стороны рамки b, т.е. 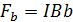(направления этих сил 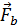показано на рис.1).

Ясно, что результирующая сила Ампера, действующая на рамку, равна нулю, и рамка будет оставаться в покое.

Пусть теперь плоскость рамки с током I параллельна силовым линиям поля (параллельна вектору ).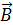

 

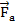
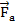
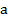
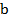
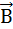
Рис.2

 

В этом случае сила Ампера (рис. 2) действует только на стороны рамки a. Две равные силы 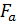, действующие на эти стороны, образуют пару сил. Появляется вращательный момент пары сил:

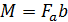, (4)

где b – плечо пары сил. Подставляя (3) в (4), получаем

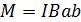(5)

Но 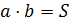(площадь, охватываемая рамкой с током), следовательно,

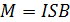(6)

Из (6) видно, что вращающий момент пропорционален силе тока I в рамке и площади рамки. Таким образом, действие магнитного поля на плоский контру с током определяется величиной

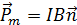, (7)

которую называют магнитным моментом контура. (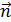 - единичный вектор нормали). Единицей измерения момента является ампер-квадратный метр (А⋅м²).

Ориентацию рамки в пространстве принято характеризовать направлением положительной нормали 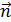к рамке, связанной с направлением тока в рамке правилом правого винта (рис.3).

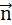
Рис.3 Положительная нормаль к рамке с током.

 

Вращающий момент (6) стремится повернуть рамку так, чтобы она заняла равновесное положение (рис.1), при котором М=0.

Имея ввиду (7), окончательно вращающий момент, действующий на рамку с током в магнитном поле, можно представить в виде:

,

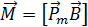или в скалярной форме

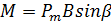(8)

Здесь β – угол между положительной нормалью к рамке с током и направлением вектора 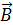магнитного поля.

Отметим, что полученное выражение (8) для вращающего момента 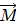справедливо для плоского контура любой формы.