2018-01-08
327
Предположим, инвестор решает задачу об оптимальном вложении капитала в набор n видов ценных бумаг. Известен размер прибыли 
, получаемой, если вложить весь капитал в ценные бумаги вида 
, где 
. Структура портфеля ценных бумаг определяется набором долей 
, 
вложения капитала в бумаги вида , т.е. набором неотрицательных чисел, удовлетворяющих условию 
. Ожидаемая прибыль 
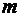является случайной величиной вида 
и является выпуклой линейной комбинацией величин 
в соответствии с их долями. По условию, прибыль должно быть не меньше заданной нижней границы 
, т.е. 
. При этом должен быть минимизирован финансовый риск вложения капитала, определяемый величиной дисперсии 
размера ожидаемой прибыли. Так как случайная величина прибыли является линейной комбинацией заданных случайных величин с числовыми коэффициентами , то указанная дисперсия вычисляется по формуле
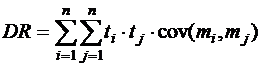, (1)
где ковариация 
случайных величин 
вычисляется по формуле 
и для случая i=j совпадает с их дисперсией. Формула (1) может быть записана в матричном виде:
, (2)
где 
вектор долей, 
результат его транспонирования,
- матрица ковариаций случайных величин . На практике матрица 
может быть получена в результате эконометрических исследований инвестора или из справочных данных. Например, очень часто оказывается, что случайные величины некоррелированны (вложение капитала в ценные бумаги вида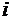 
не влияет на вложение капитала в ценные бумаги типа 
), т.е. =0, если 
В этом случае матрица 
является диагональной, причем по диагонали расположены дисперсии случайных величин . С учетом сформулированных условий, задача выбора оптимального портфеля ценных бумаг имеет вид:
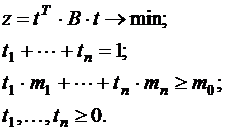(3)
Задача (3)- это задача квадратического программирования с двумя линейными ограничениями и условиями неотрицательности переменных . В общем случае каноническая задача квадратического программирования записывается в виде
(4)
Здесь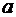 
- число, 
- вектор неизвестных, 
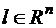- вектор линейной формы квадратической функции, 
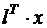- линейная форма, входящая в состав квадратической функции, 
- квадратическая форма, входящая в состав квадратической функции, 
- матрица квадратичной формы, симметрическая квадратная матрица,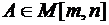 
- матрица коэффициентов линейных ограничений, 
- вектор правых частей линейных ограничений. С помощью введения новых переменных и изменения обозначений изучаемая задача (3) может быть приведена к каноническому виду (4). Пусть инвестор имеет возможность вложить капитал в ценные бумаги с отдачей . Тогда задача оптимизации портфеля ценных бумаг может быть записана в виде
(5)
Если инвестор имеет возможность вложить долю 
капитала в сферу с гарантированной (но относительно малой) отдачей 
, тогда задача оптимизации портфеля ценных бумаг может быть записана в виде
(6)
В качестве характеристики решения задачи об оптимизации портфеля инвестиций можно использовать доверительный интервал с уровнем доверия P для величины ожидаемой прибыли. Предполагая случайные величины нормально распределенными, получаем, что доверительный интервал 
, где
- значение интегральной функции Лапласа.
Примечание: В выводах по найденному оптимальному решению указать математическое ожидание прибыли, дисперсию прибыли, структуру портфеля инвестиций, доверительный интервал с уровнем доверия P=0.95 для ожидаемой прибыли.
