А=  [1.10]- основная матрица, её элементами являются коэффициенты при неизвестных;
[1.10]- основная матрица, её элементами являются коэффициенты при неизвестных;
В=  [1.11]- матрица столбец свободных членов; Х=
[1.11]- матрица столбец свободных членов; Х=  [1.12]- матрица столбец неизвестных; С=
[1.12]- матрица столбец неизвестных; С=  [1.13]- расширенная матрица.
[1.13]- расширенная матрица.
Пример
 , А=
, А=  - основная матрица;
- основная матрица;
В=  - матрица столбец свободных членов; Х=
- матрица столбец свободных членов; Х=  - матрица столбец неизвестных; С=
- матрица столбец неизвестных; С=  - расширенная матрица.
- расширенная матрица.
Решение систем линейных уравнений матричным методом
 , А=
, А=  - основная матрица; В=
- основная матрица; В=  - матрица столбец свободных членов; Х=
- матрица столбец свободных членов; Х=  - матрица столбец неизвестных.
- матрица столбец неизвестных.
Х= А-1В [1.14]- формула для решения систем линейных уравнений матричным методом.
Пример
1)  , А=
, А=  , В=
, В=  , Х=
, Х=  , А-1=
, А-1= 
 ;
;
применим формулу: Х= А-1В= 

 =
=  , значит х=2, у=1.
, значит х=2, у=1. 
2)  , А=
, А= 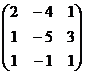 , В=
, В=  , Х=
, Х=  , А-1=-
, А-1=- 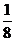
 ;
;
применим формулу: Х= А-1В=- 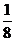

 =
=  , значит х1=2, х2=0, х3=-1.
, значит х1=2, х2=0, х3=-1.
Решение систем линейных уравнений методом Крамера
Для решения система n линейных уравнений с n неизвестными применяются формулы: х1=  , х2=
, х2=  , …, хn=
, …, хn=  [1.15]; где х1, х2, …, хn- неизвестные, Д- определитель основной матрицы; ДХ1- определитель основной матрицы в котором первый столбец заменили столбцом свободных членов, ДХ2- определитель основной матрицы в котором второй столбец заменили столбцом свободных членов, …., ДХn- определитель основной матрицы в котором n-ый столбец заменили столбцом свободных членов.
[1.15]; где х1, х2, …, хn- неизвестные, Д- определитель основной матрицы; ДХ1- определитель основной матрицы в котором первый столбец заменили столбцом свободных членов, ДХ2- определитель основной матрицы в котором второй столбец заменили столбцом свободных членов, …., ДХn- определитель основной матрицы в котором n-ый столбец заменили столбцом свободных членов.
Частные случаи
1) Пусть Д≠0, ДХ1≠0, ДХ2≠0, …, ДХn≠0- тогда система имеет единственное решение.
2) Пусть Д=0, ДХ1≠0, ДХ2≠0, …, ДХn≠0- тогда система не имеет решений.
3) Пусть Д=0, ДХ1=0, ДХ2=0, …, ДХn=0- тогда система имеет бесконечное множество решений (см. метод Гаусса).
 2018-01-08
2018-01-08 1398
1398
