Свойства определителей. 1) Значение определителя не изменится при замене всех строк соответствующими столбцами и наоборот: =а11а22-а21а12; = а11а22-а21а12

1) Значение определителя не изменится при замене всех строк соответствующими столбцами и наоборот: =а₁₁а₂₂-а₂₁а₁₂; 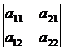= а₁₁а₂₂-а₂₁а_12.

Пример

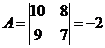
2) Если поменять местами две строки или два столбца определителя, то он изменит знак на противоположный: =а₁₁а₂₂-а₂₁а₁₂;

= а₂₁а₁₂- а₁₁а₂₂=- а₁₁а₂₂-а₂₁а₁₂.

Пример

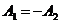
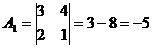
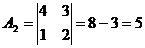
3) Определитель с двумя равными строками или столбцами равен нулю.

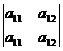=а₁₁а₁₂- а₁₁а₁₂=0.

4) Если умножить элементы, какой- либо строки или столбца на λ≠0, λ=conct, то определитель увеличится в λ раз: 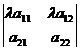= λа₁₁а₂₂- λа₂₁а₁₂= λ(а₁₁а₂₂-а₂₁а₁₂).

Пример

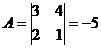
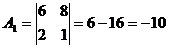
5) Если все элементы строки или столбца определителя равны нулю, то весь определитель равен нулю: = а₁₁0- а₂₁0=0.

6) Определитель не изменится, если прибавить к элементам некоторой строки (столбца) элементы другой строки (столбца) умноженные на λ≠0, λ=conct:

=а₁₁а₂₂-а₂₁а₁₂,

=а₂₂(а₁₁+ λа₂₁)-а₂₁(а₁₂+ λа₂₂)= а₂₂а₁₁+ а₂₂ λа₂₁- а₂₁ а₁₂-

-а₂₁ λа₂₂= а₁₁а₂₂-а₂₁а₁₂.

Пример

(к 2 строке + 1 строку)

(к 1 столбцу + 2 столбец)

Минор и алгебраическое дополнение

 

Минором М_ij элемента а_ij называется определитель n-1-го порядка, полученный из определителя n-го порядка, вычеркиванием i-ой строки и j-го столбца.

Пример

а) А= 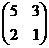, М₁₁=1, М₁₂=2, М₂₁=3, М₂₂=5.

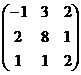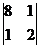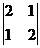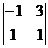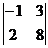б) В= , М₁₁= =15, М₁₂= =3, М₁₃= =-6, М₂₁= =4, М₂₂= =-4, М₂₃= =-4, М₃₁= =-13, М₃₂= =-5, М₃₃= =-14.

Алгебраическим дополнением А_ij элемента а_ij называется выражение равное

А_ij=(-1)^i+jМ_ij А₁₁=(-1)¹⁺¹М₁₁ А₁₂=(-1)¹⁺²М₁₂

Пример

А= 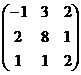, А₁₁=(-1)²М₁₁=15, А₁₂=(-1)³М₁₂=-3, А₁₃=(-1)⁴М₁₃=-6, А₂₁=(-1)³М₂₁=-4, А₂₂=(-1)⁴М₂₂=-4, А₂₃=(-1)⁵М₂₃=4, А₃₁=(-1)⁴М₃₁=-13, А₃₂=(-1)⁵М₃₂=5,А₃₃=(-1)⁶М₃₃=-14.

 

 

Невырожденные матрицы

Обратная матрица

Квадратная матрица называется невырожденной, если её определитель не равен нулю.

Матрица А^-1, удовлетворяющая условию А А^-1= А^-1А=Е [1.7], называется обратной матрицей к матрице А.

Обратная матрица вычисляется по формуле: А^-1= [1.8], где Д_А- определитель матрицы А,

А^*- присоединённая матрица её элементами являются алгебраические дополнения А^Т.