Действия над матрицами. Всё что выделено красным, это для самост.изучения

Всё что выделено красным, это для самост.изучения

Глава I. Линейная алгебра

Матрицы

Матрицы. Виды матриц.

Матрицей называется упорядоченная таблица чисел, состоящая из m строк и n столбцов.

Число строк и столбцов (m n) называется размером матрицы.

а_ij называется элементом матрицы, где i-номер строки, j-номер столбца матрицы.

Пример

а) А= размер матрицы 2 2, а₁₁=1, а₂₁=3.

б) В= размер матрицы 4 3, а₃₃=13, а₄₁=4, а₁₂=0.

Виды матриц

Матрица называется квадратной, если в ней число строк равно числу столбцов.

Если в матрице число строк не равно числу столбцов, то такая матрица называется прямоугольной.

Пример

А= -квадратная матрица; В= -прямоугольная матрица.

Матрица, элементы которой составляют строку, называется матрица строка.

Матрица, элементы которой составляют столбец, называется матрица столбец.

Пример А= 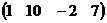- матрица строка; В= - матрица столбец.

Главная диагональ квадратной матрицы - это диагональ, которая начинается с элемента а₁₁.

Квадратная матрица, у которой на главной диагонали единицы, а все остальные элементы равны нулю, называется единичной матрицей.

Матрица, у которой все элементы равны нулю, называется нулевой матрицей.

Пример

Е= - единичная матрица; О= - нулевая матрица.

Матрица, в которой строки и столбцы заменены местами, называется транспонированной матрицей А^т.

Пример

Если А= , тогда А^т= .

Действия над матрицами

Равенство матриц.

Две матрицы называются равными, если они одного размера и равны их соответствующие элементы.

Пусть А= , В= , тогда А=В, если а_ij=в_ij.

Сложение матриц.

При сложении матриц (одного размера) складываются их соответствующие элементы.

Пусть А= , В= , А+В=С, С= , где с_ij= а_ij+в_ij. [1.1]

Пример

А= , В= , А+В= .