Способ угловой засечки применяют для разбивки недоступныхточек, находящихся на значительном расстоянии от исходныхпунктов.
Различают прямую и обратную угловые засечки.
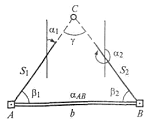
В способе прямой угловой засечки положение наместности проектной точки С (рис. 1) находят отложением наисходных пунктах А и В проектных углов β1 и β2.
 На точность разбивки способом прямой угловой засечки оказывают влияние погрешности: собственно прямой засечки тсз, исходных данных тИСХ, центрирования теодолита и визирных целей т ц, фиксации разбивочной точки, т.е.
На точность разбивки способом прямой угловой засечки оказывают влияние погрешности: собственно прямой засечки тсз, исходных данных тИСХ, центрирования теодолита и визирных целей т ц, фиксации разбивочной точки, т.е.
тС2 = тсз2 + тИСХ2 + т ц 2 + тф2
Рис. 1 Схема разбивкиСредняя квадратическая погрешность
способами прямой собственно засечки
угловой и линейной тсз= 
засечекили
тсз= 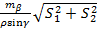
где тβ - средняя квадратическая погрешность отложения углов β1 и β2.
тИСХ = 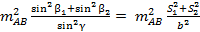
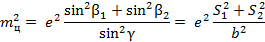
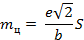
где е — величина линейного элемента центрирования.
Распределив невязку в треугольникепоровну на все три угла, определяют координаты точки С. Сравнивая их с проектными значениями, находят поправки (редукции), по которым в натуре смещают(редуцируют) 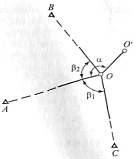 приближенно вынесенную точку С. Такой способ называют способом замкнутого треугольника.
приближенно вынесенную точку С. Такой способ называют способом замкнутого треугольника.
На принципе редуцирования основано и применение для разбивки способа обратной угловой засечки (рис. 2).
На точность разбивки способом обратной угловой засечки оказывают влияние погрешности: собственно засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки и редуцирования. Рис. 2 Схема способа
Погрешность собственно обратной засечки обратной угловой может быть подсчитана по приближенной формуле засечки
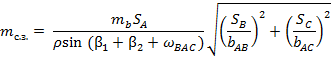
где S — расстояние от определяемого до соответствующих опорных пунктов; b — расстояние между соответствующими опорными пунктами; 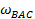 — угол между исходными сторонами.
— угол между исходными сторонами.
Если для приближенных расчетов принять SA = SB = SC = S ср; 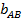 =
= 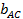 = bср, то формула
= bср, то формула
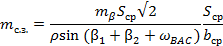
Погрешности исходных данных учитывают по формуле
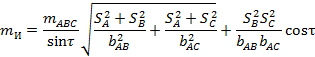
где тА = тB = тC = тАВС — погрешность в положении исходногопункта;  =
= 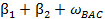 - 180°.
- 180°.
Для приближенных расчетов
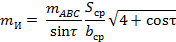
 2018-01-08
2018-01-08 599
599








