2020-01-14
154
Рассмотрим квадратный трехчлен 
.
Квадратный трехчлен - это многочлен второй степени. Значения 
, при которых квадратный трехчлен обращается в нуль, называются корнями квадратного трехчлена. Для нахождения корней квадратного трехчлена нужно решить квадратное уравнение 
.
Мы уже знаем, что число действительных корней квадратного уравнения, а значит, и квадратного трехчлена зависит от знака дискриминанта 
. Пусть дан квадратный трехчлен 
с неотрицательным дискриминантом 
.
Теорема. Если 
и 
- корни квадратного трехчлена , то 
. (1)
Доказательство. Так как и - корни квадратного уравнения 
с дискриминантом 
, то по теореме Виета
, 
.
Поэтому
.
Полученное равенство (1) называется формулой разложения квадратного трехчлена на линейные множители. [5, c.129]
Пример 1. Упростить выражение 
.
Решение. Для квадратного трехчлена 
дискриминант 
. Найдем корни трехчлена, решив квадратное уравнение 
. Получим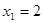 
и 
. Поэтому по формуле (1) 
. Следовательно,
. [2, c.121]
Пример 2. Доказать, что выражение
|
|
|
при всех допустимых значениях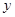 
есть величина постоянная.
Решение. 1) Разложим знаменатель второй дроби на линейные множители. Решив уравнение 
, найдем 
, 
. Получаем разложение квадратного трехчлена: 
.
2) 
;
3) 
;
4) 
- величина, постоянная при всех допустимых значениях 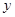(т.е. при любых значениях 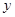, для которых 
, 
, 
). [5, c.130]
