Найдя дифференциал dy данной функции 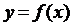 , можем затем найти дифференциал от этого дифференциала. Тем самым получим так называемый дифференциал второго порядка
, можем затем найти дифференциал от этого дифференциала. Тем самым получим так называемый дифференциал второго порядка 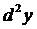 данной функции
данной функции 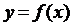 :
:
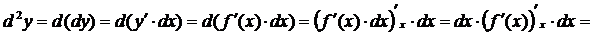
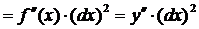 .
.
Итак, если 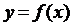 – некоторая дважды дифференцируемая функция, то ее дифференциал второго порядка
– некоторая дважды дифференцируемая функция, то ее дифференциал второго порядка 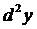 (дэ два игрек) находится по формуле:
(дэ два игрек) находится по формуле:
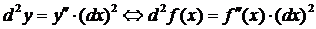 (7)
(7)
Отсюда, кстати, получаем:
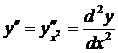 , где
, где 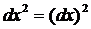 (8)
(8)
Тем самым находит свое оправдание обозначение Лейбница (1) для производной второго порядка функции 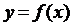 . Аналогично получает оправдание и обозначение (2) для производной третьего порядка, которая выражается через дифференциал
. Аналогично получает оправдание и обозначение (2) для производной третьего порядка, которая выражается через дифференциал 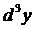 (дэ три игрек) третьего порядка
(дэ три игрек) третьего порядка
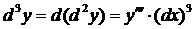 , откуда
, откуда 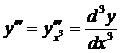 , (9)
, (9)
и т.д.
Отметим еще одно существенное обстоятельство. Дифференциал dy функции y (дифференциал первого порядка), как показано выше, имеет инвариантную (неизменную) форму 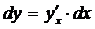 независимо от того, является ли аргумент x функции y независимой переменной или, наоборот, сам является функцией от другой переменной. А вот для дифференциалов высших порядков (
независимо от того, является ли аргумент x функции y независимой переменной или, наоборот, сам является функцией от другой переменной. А вот для дифференциалов высших порядков (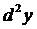 ,
, 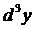 , …) эта инвариантность места не имеет.
, …) эта инвариантность места не имеет.
Действительно, пусть 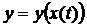 – сложная функция от t. Тогда, согласно инвариантности формы первого дифференциала dy, имеем:
– сложная функция от t. Тогда, согласно инвариантности формы первого дифференциала dy, имеем:
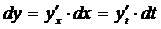 .
.
А вот
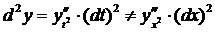 (10)
(10)
Действительно,
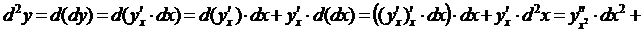
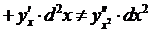
Упражнения
1. Найти дифференциалы первого и второго порядков следующих функций:
а) 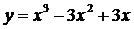 ; б)
; б) 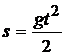 ; в)
; в) 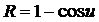 , где u – дифференцируемая функция некоторой независимой переменной.
, где u – дифференцируемая функция некоторой независимой переменной.
Ответ:
а) 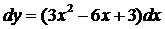 ;
; 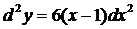 .
.
б) 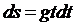 ;
; 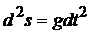 .
.
в) 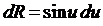 ;
; 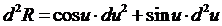 .
.
2. С помощью приближенной формулы 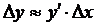 найти абсолютную и относительную погрешности вычисления объема куба со стороной x, если при измерении x допущена ошибка
найти абсолютную и относительную погрешности вычисления объема куба со стороной x, если при измерении x допущена ошибка  .
.
Ответ: 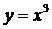 ;
;
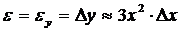 – абсолютная погрешность;
– абсолютная погрешность;
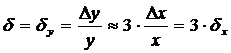 – относительная погрешность.
– относительная погрешность.
 2018-01-08
2018-01-08 500
500








