Лекция 25. Некоторые теоремы о дифференцируемых функциях. Правило Лопиталя. Производные высших порядков. Формула Тейлора. Разложение функций по формуле Тейлора.
Некоторые теоремы о дифференцируемых функциях.
Теорема Ролля: (теорема о корнях производной)
Если функция f(x) непрерывна на отрезке 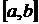 , дифференцируема во всех внутренних точках этого отрезка и на концах x=a и x=b обращается в нуль f(a)=f(b)=0, то существует внутри отрезка
, дифференцируема во всех внутренних точках этого отрезка и на концах x=a и x=b обращается в нуль f(a)=f(b)=0, то существует внутри отрезка 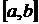 по крайней мере одна точка x=с, a<c<b, в которой производной
по крайней мере одна точка x=с, a<c<b, в которой производной 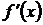 обращается в нуль, т.е.
обращается в нуль, т.е. 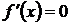 .
.
(см. рис.1)

Геометрическое истолкование: если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ох в точках с абсциссами a и b, то на этой кривой найдется по крайней мере одна точка с абсциссой с, 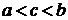 , в которой касательная параллельна оси Ох.
, в которой касательная параллельна оси Ох.
Теорема Лагранжа: (теорема о конечных приложениях)
Если функция f(x) непрерывна на отрезке 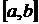 , дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка
, дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка 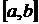 найдется по крайней мере одна точка с, a<c<b, что
найдется по крайней мере одна точка с, a<c<b, что 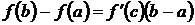 . (см. рис.2)
. (см. рис.2)
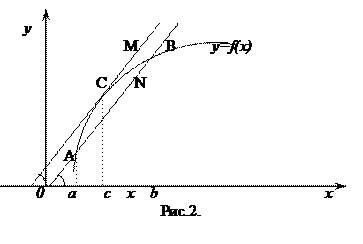
Геометрическое истолкование: если во всех точках дуги AB существует касательная, то на этой дуге найдется точка С между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.
Теорема Коши: (теорема об отношении приращений двух функций)
Если f(x) и 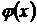 - две функции, непрерывные на отрезке
- две функции, непрерывные на отрезке 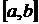 и дифференцируемых внутри него, причем
и дифференцируемых внутри него, причем 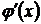 нигде внутри отрезка не обращается в нуль, то внутри отрезка
нигде внутри отрезка не обращается в нуль, то внутри отрезка 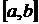 найдется по крайней мере одна точка с, a<c<b, что
найдется по крайней мере одна точка с, a<c<b, что 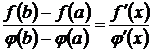 .
.
 2018-01-08
2018-01-08 429
429







