Если 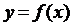 – уравнение движения точки по ее траектории, то, как мы знаем, ее производная
– уравнение движения точки по ее траектории, то, как мы знаем, ее производная  (производная первого порядка) представляет собой скорость v (x) движения точки (мгновенную скорость движения). Но тогда производная второго порядка
(производная первого порядка) представляет собой скорость v (x) движения точки (мгновенную скорость движения). Но тогда производная второго порядка  будет иметь смысл «скорость изменения скорости» движения точки. В физике такая величина называется ускорением. Поэтому
будет иметь смысл «скорость изменения скорости» движения точки. В физике такая величина называется ускорением. Поэтому
 (3)
(3)
– ускорение движения точки в момент x. В этом и состоит физический смысл производной второго порядка.
Пример 4. Как известно, уравнение движения свободно падающего в безвоздушном пространстве тела, начавшего свое падение в момент  , имеет вид:
, имеет вид: 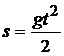 (s – путь, пройденный падающим телом за время t). Найдем скорость
(s – путь, пройденный падающим телом за время t). Найдем скорость  и ускорение
и ускорение 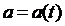 падающего тела:
падающего тела:
 ;
;
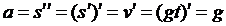 .
.
То есть ускорение a падающего тела неизменно и равно g – ускорению свободного падения (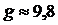 м/сек2). А скорость v падающего тела возрастает пропорционально времени по формуле
м/сек2). А скорость v падающего тела возрастает пропорционально времени по формуле 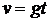 .
.
Упражнения
1. Найти угол наклона к оси ох касательной, проведенной к параболе 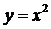 в точке
в точке  .
.
Ответ: 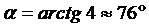 .
.
2. Найти на параболе 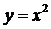 такую точку
такую точку 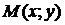 , чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол
, чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол  .
.
Ответ:  .
.
3. В момент времени  найти скорость v и ускорение a точки, движущейся по оси ох по закону
найти скорость v и ускорение a точки, движущейся по оси ох по закону 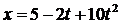 .
.
Ответ: 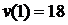 ;
;  .
.
4. Найти производную 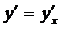 функций:
функций:
а) 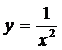 ; б)
; б) 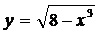 ; в)
; в) 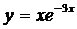 ; г)
; г)  ; д)
; д) 
Ответ: а) 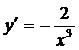 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
5. Найти производную  функций:
функций:
а) 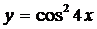 ; б)
; б)  ; в)
; в)  .
.
Ответ: а) 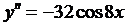 ; б)
; б) 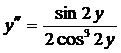 ; в)
; в) 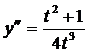 .
.
Правило Лопиталя вычисления пределов.
Это правило состоит в следующем. Если требуется найти предел вида
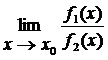 , (4)
, (4)
где x0 – число или символ  , и этот предел приводит к неопределенности вида
, и этот предел приводит к неопределенности вида 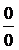 или
или 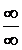 , то
, то
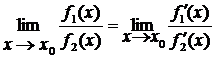 , (5)
, (5)
Словесная формулировка правила Лопиталя (5) такова: предел отношения бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует.
Доказательство. Исчерпывающее доказательство правила Лопиталя довольно громоздко. В связи с этим ограничимся рассмотрением случая, когда предел (4) приводит к неопределенности вида 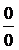 :
:
 ;
;  ;
;  . (6)
. (6)
При этом будем считать, что x 0 – некоторое конечное число.
Если функции  и
и  непрерывны в точке x 0, то в силу определения непрерывности функций верны следующие равенства
непрерывны в точке x 0, то в силу определения непрерывности функций верны следующие равенства  и
и  . Если же эти функции в точке x 0 разрывны, то их значения при x 0 не равны нулю (у них другие значения или они там вообще не определены). Тогда переопределим (или доопределим) их в точке x 0 так, чтобы стало
. Если же эти функции в точке x 0 разрывны, то их значения при x 0 не равны нулю (у них другие значения или они там вообще не определены). Тогда переопределим (или доопределим) их в точке x 0 так, чтобы стало  и
и  . После этого, в силу того же определения непрерывности функций, функции
. После этого, в силу того же определения непрерывности функций, функции  и
и  станут непрерывными в точке x 0. Далее, будем считать, что обе эти функции будут непрерывно дифференцируемыми в окрестности точки х0, включая саму точку х0, причем
станут непрерывными в точке x 0. Далее, будем считать, что обе эти функции будут непрерывно дифференцируемыми в окрестности точки х0, включая саму точку х0, причем  . Тогда получим:
. Тогда получим:
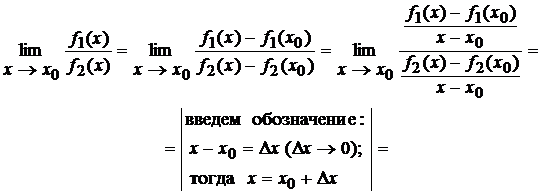


Примечание. Предел отношения производных, стоящий в правой части равенства (5), тоже может приводить к неопределенности вида 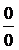 или
или 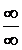 . Тогда правило Лопиталя можно применить и к нему. То есть применить это правило повторно.
. Тогда правило Лопиталя можно применить и к нему. То есть применить это правило повторно.
Пример 5.
 .
.
Пример 6.

Пример 7.
 .
.
Пример 8.
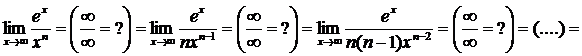
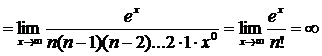 .
.
Последние два примера показывают, что при 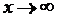
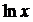 растет несравненно медленнее, чем x, а
растет несравненно медленнее, чем x, а  – несравненно быстрее, чем
– несравненно быстрее, чем 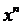 при любом значении n.
при любом значении n.
Пример 9.

Пример 10.  .
.
Для вычисления этого предела введем обозначение:  . Тогда
. Тогда  . Учитывая, что
. Учитывая, что 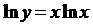 , находим:
, находим:

Итак, 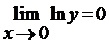 . То есть при
. То есть при  и
и  , а значит,
, а значит, 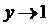 , ибо
, ибо  . Таким образом,
. Таким образом, 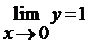 , а значит,
, а значит, 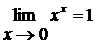 .
.
Упражнения
1. С помощью правила Лопиталя найти пределы:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
Ответ: а) 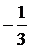 ; б)
; б) 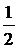 ; в)
; в)  ; г) 2; д)
; г) 2; д)  .
.
2. С помощью правила Лопиталя доказать второй замечательный предел:
 .
.
3. С помощью правила Лопиталя доказать, что при  и любом n
и любом n
 .
.
 2018-01-08
2018-01-08 846
846








