Закон больших чисел – это
действия над большими числами
правила выполнения арифметических действий над большими числами
закон распределения большого числа случайных величин
+группа теорем о средних характеристиках случайных величин при большом числе испытаний
Последовательность случайных величин  называется сходящейся по вероятности при
называется сходящейся по вероятности при  к случайной величине Х, если при любом сколь угодно малом
к случайной величине Х, если при любом сколь угодно малом 
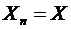

+ 

Лемма Маркова оценивает вероятность того, что положительная случайная величина Х не превзойдет
ее дисперсии
ее среднего квадратического отклонения
предельной ошибки
+  - кратного математического ожидания
- кратного математического ожидания
Из обобщенной теоремы Чебышева следует, что если дисперсии попарно независимых случайных величин ограничены сверху константой  , то
, то
средняя арифметическая случайных величин равна средней арифметической их математических ожиданий
средняя арифметическая случайных величин равна математическому ожиданию одной из них
средняя арифметическая случайных величин больше средней арифметической их математических ожиданий
+ средняя арифметическая случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий
Из обобщенной теоремы Чебышева следует, что 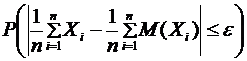
равна 1
равна 0
+больше, чем 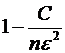
равна 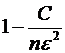
Неравенство Чебышева оценивает вероятность того, что отклонение случайной величины Х от ее математического ожидания
положительно
отрицательно
+по абсолютной величине не превзойдет определенного положительного числа 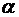
по абсолютной величине превзойдет определенное положительное число 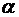
Из неравенства Чебышева с вероятностью, большей, чем  можно утверждать, что абсолютная величина отклонения случайной величины Х от ее математического ожидания
можно утверждать, что абсолютная величина отклонения случайной величины Х от ее математического ожидания
больше, чем 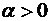
+не превзойдет 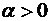
равна 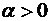
равна 0
 2018-01-08
2018-01-08 684
684







