промежуточному аргументу, умноженной на дифференциал
этого аргумента.
Доказательство. Пусть y=f(u) и u=j(x),тогда
dy=y¢u×du
По правилу дифференцирования сложной функции
y¢=y¢u×u¢x и dy=y¢u×u¢x×dx,но
u¢x×dx=du Þ
dy=y¢u×du
Это свойство дифференциала называют инвариантностью, то есть неизменностью формы записи дифференциала для простой и сложной функций.
Благодаря этому свойству формулы дифференцирования основных функций оказываются одними и теми же как для простых, так и для сложных функций.
Сводка правил и формул нахождения дифференциалов.
Правила
1. dc=0
2. d(u+v)=du+dv
3. d(u×v)=du×dv
4. d(c×u)=c×du
5. 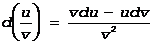
Формулы
1. d(au)=aulna×du; deu=eu×du
2. 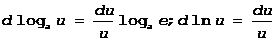
3. d(um)=m×um-1du
4. d(sin u)=cos u×du; d(cos u)=-sin u×du;
5. 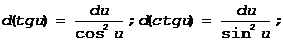
6. 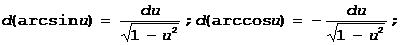
7. 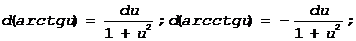
Для получения этих формул достаточно было умножить равенства в формулах дифференцирования на dx и заменить u¢dx и v¢dx на du и dv.
Из формулы для нахождения дифференциала следует, что
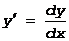
Поэтому этот символ 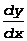 используют наряду с y¢ и f¢(x).
используют наряду с y¢ и f¢(x).
Производные и дифференциалы высших порядков.
Пусть задана любая дифференцируемая f(x). y¢=f¢(x) есть также функция x. Поэтому можно ставить вопрос об отыскании производной и от этой функции.
Определение. Производную от производной данной функции, если она существует, называют производной второго порядка или второй производной и обозначают символом y¢¢=f¢¢(x).
Таким образом (y¢)¢=y¢¢=f¢¢(x).
В связи с этим y¢=f¢(x) в дальнейшем будем называть производной первого порядка или первой производной.
Вторая производная имеет простой механический смысл. Если задан закон прямолинейного движения материальной точки S=f(t) Þ v=S¢=f¢(t)
- есть мгновенная скорость движения.
Вторая же производная от пути по времени, как производная от скорости, есть скорость изменения скорости движения, то есть ускорение
w =v¢=S¢¢=f¢¢(t).
Аналогично можно ввести производные более высоких порядков: y¢¢¢ - производная 3-го порядка, y(IV) - 4-го и так далее.
Вообще говоря производной порядка n+1 от f(x) называют производную от производной n -го порядка для f(x):
(y(n))¢=y(n+1)= f(n+1)(x)
В силу принятого определения производная m порядка от производной n порядка равна производной n+m порядка (при условии существования всех производных):
(y(n)) (m)=y(n+m)= f(n+m)(x)
Примеры.
1. y=ek×x Þ y(n)=knek×x
2. y=sin x, y¢=cos x=sin(x+p/2) Þ y¢¢=(sin(x+p/2))¢= sin(x+p/2+p/2) … y(n)=sin(x+p×n/2)
Аналогично, (cos x)(n)=cos(x+p×n/2)
3. 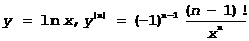
4. y=xn, nÎN, Þ y(n)=n!
5.
В При дифференцировании неявно заданных функций F(x,y) мы установили, что
y¢ =Ф(x,y)
Так как y¢¢=(y¢)¢ Þ y¢¢= Ф¢(x,y(x)),то есть нужно взять производную от Ф по x, считая y=y(x). В результате мы получим
y¢¢=y(x,y,y¢)=y(x,y,Ф(x,y))=y(x,y),
то есть опять y¢¢ будет функцией только x и y. Этот процесс, при условии существования всех производных, может быть продолжен.
С Пусть теперь функция задана параметрически:
y=y(y), x=j(t) Þ
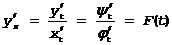
Так как y¢¢xx=(y¢x)¢x, то вопрос сводится к отысканию производной по x от y¢x=F(t), когда x=j(t), то есть опять от функции, заданной параметрически: Применяя правило вторично, получим
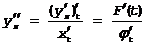
Для отыскания производных 3-го и более высших порядков поступают аналогично:
Пример. x=a(t-sin t), y=a(1-cos t), y¢¢=?, y¢¢¢=?.
Дифференциалы высших порядков.
Дифференциалы высших порядков определяются аналогично производным высших порядков.
Определение. Дифференциалом 2-го порядка (d2y) от f(x) называют дифференциал от ее дифференциала:
d2y=d(dy)
Найдем его выражение через производную. Так как dy=y¢dx Þ (dx не зависит от x и следовательно dx есть постоянная относительно x и (dx)¢=0)
d2y=d(dy)=d(y¢dx)=(y¢dx)¢×dx=(y¢)¢×dx×dx=y¢¢ dx2.
Таким образом второй дифференциал от f(x) есть произведение f¢¢(x) на квадрат dx - dx2
d2y=y¢¢×dx2
Аналогично вводятся дифференциалы высших порядков.
d(n+1)y=d(dny)
Методом индукции можно доказать, что
d(n)y= y(n)(dxn) Þ 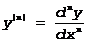
Последнее обозначение эквивалентно y(n), f(n)(x) и тому подобному.
Дифференциалы, начиная со 2-го порядка, не обладают свойством инвариантности. Пусть y=f(u) и u=j(x) Þ dy=y¢udu
Так как u=j(x) Þ du=u¢xdx есть также функция x Þ
d2y=d(y¢u)=d(y¢u)du+y¢ud(du)=y¢¢udu2+y¢ud2u
Таким образом в выражении d2y появляется дополнительное слагаемое.
Формула Лейбница
В заключение этого раздела приведем формулу Лейбница, которая позволяет вычислить производную или дифференциал n -го порядка от произведения 2-х функций.
y=u×v
y¢=u¢×v+v¢×u
y¢¢=u¢¢×v+2×u¢v¢+v¢¢×u
y¢¢¢=u¢¢¢×v+3×u¢¢v¢+3×u¢v¢¢+v¢¢¢×u
…..
Отсюда вытекает общее формальное правило:
Чтобы найти производную (дифференциал) от (u×v)(n) надо по формуле бинома Ньютона разложить n -ю степень суммы (u+v)n и затем заменить показатели степеней u и v указателями порядка производных, причем нулевые степени (u0 и v0),входящие в крайние члены разложения заменить самими функциями u и v (то есть, «производными нулевого порядка»).
Для дифференциала n -го порядка справедлива формула
dn(u×v)=(u×v)(n)×dxn
dy=v×du+u×dv
d2y=v×d2u+2×du×dv+u×d2v
d3y=v×d3u+3×d2u×dv+3×du×d2v +u×d3v и т.п.
Применение производных к исследованию свойств функций.
Возрастание и убывание функций.
Экстремум.
Определение1. Функция y=f(x) называется возрастающей в промежутке (a,b), если для любых x1, x2 Î (a,b) большему из них соответствует и большее значение функции.
x1 Î (a,b), x2 Î (a,b), x2>x1 Þ f(x2)>f(x1)
Определение 2. Функция y=f(x) называется убывающей на (a,b), если для любых x1, x2 Î (a,b) большему x соответствует меньшее значение f(x).
x1 Î (a,b), x2 Î (a,b), x2>x1 Þ f(x2)<f(x1)
Из этих определений следует, что для возрастающих функции sign(Dy)=sign(Dx), в силу чего их отношение положительно:
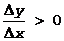
Для убывающей функции sign(Dy)=-sign(Dx) Þ
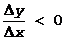
Если функция на переходит от возрастания к убыванию, или наоборот, ее называют колеблющейся на (a,b).
Значения x, при которых f(x) достигает своих наибольших или наименьших значений по сравнению с соседними, называют точками максимума и минимума.
Определение 3. x=x0 -точка максимума f(x), а f(x0) - максимум функции, если существует некоторая окрестность x0 (т.е. x0-d, x0+d) такая, что значение функции в любойточке x1 Î(x0-d, x0+d) будет меньше, чем ее значение в x0, то есть меньше, чем максимум f(x0)
f(x0+Dx)<f(x0) прилюбом |Dx|<d
Аналогично определяются точки максимума и минимума функции
f(x0+Dx)>f(x0) прилюбом |Dx|<d
Дать графические примеры.
Точки минимума и максимума объединяются под общим названием – точки экстремума (экстремальные точки), а минимум и максимум функции – экстремумы функции.
Экстремумы функции, определенные выше, часто называют строгими экстремумами, в отличие нестрогих
f(x0+Dx)£f(x0) и f(x0+Dx)³f(x0)
Из определения вытекает, что вне d-окрестности x0 значения f(x) могут быть любыми, по отношению к f(x0).
Например за пределами (x0-d, x0+d), f(x+Dx)>f(x0) – где x0 - точка максимума, и аналогично f(x+Dx)<f(x0), если x0 - точка минимума f(x).
Таким образом понятия максимальной и минимальной функции носят локальный (местный) характер. Далее мы установим признаки возрастания и убывания функций и признаки экстремума функций, основанные на понятии производной.
Теоремы Ферма, Ролля, Лагранжа и Коши.
Теорема Ферма. Если f(x) непрерывна на (a,b) и в x0Î(a,b) достигает максимума (минимума) и дифференцируема в x0, то ее производная в этой точке равна 0:
f¢(x0)=0
Доказательство. Допустим, что f(x0) –максимум (минимум) функции. При достаточно малых D x, точка x0+Dx независимо от знака D x.
a) Пусть D x>0 Þ 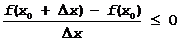 , переходя к пределу при D x®+0 получим:
, переходя к пределу при D x®+0 получим: 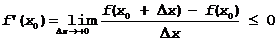 , как предел неположительной величины.
, как предел неположительной величины.
b) D x<0 Þ 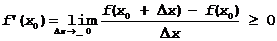
Так как для дифференцируемой в x0 функции производная слева равна производной справа Þ f¢(x0)=0, теорема доказана.
Аналогично проводится доказательство и для x0 - точки минимума, и для случая строгих неравенств.
Геометрический смысл очевиден: касательная к графику f(x) в точке экстремума, в которой f(x) дифференцируема, параллельна оси OX.
рисунок
Теорема Ролля. Если f(x) непрерывна на [a,b] и дифференцируема в (a,b), а на концах [a,b] принимает равные значения: f(a)=f(b)=c,то в промежутке (a,b) найдется точка x0 (по крайней мере одна), в которой f¢(x0)=0.
Доказательство. Рассмотрим случай f(x)ºc, xÎ[a,b], удовлетворяющий условиям теоремы: Þ f¢(x)=(c)¢=0 длялюбых x0.
Если же f(x)¹c будучи непрерывной на [a,b], она достигает своих наибольших и наименьших значений – M и m (см. свойства непрерывной функции). При этом возможны 3 случая:
a) f(a)=f(b)=m, Þ f(x) достигнет наибольшего M в x0Î(a,b), то есть внутренней точке [a,b]. В точке x0 функция дифференцируема и тогда по теореме Ферма Þ f¢(x0)=0.
b) f(a)=f(b)=M, Þ f(x) достигнет минимума в некоторой x0Î(a,b), и снова, по теореме Ферма Þ f¢(x0)=0.
c) Пусть теперь f(x) такова, что f (x0)=M и Þ f (x0 ¢ )=m, x0,x0 ¢ Î(a,b), Þ f¢(x0)=0 и f¢(x0 ¢ )=0 по теореме Ферма.
Геометрический смысл теоремы Ролля: при выполнении условий теоремы Ролля на графике f(x) найдется хотя бы одна точка x0, касательная в которой будет параллельна оси ОХ.
Нарушение хотя бы одного из условий ведет к нарушению вывода из теоремы.
Рисунок Рисунок Рисунок
В частном случае, когда f(a)=f(b)=0 теорема Ролля имеет очень полезное для приложений толкование: Между двумя нулями дифференцируемой функции всегда заключен по крайней мере один нуль ее производной, то есть эта точка может оказаться max или min.
Теорема Коши. Если f(x) и j (x) непрерывны на [a,b] и дифференцируемы в (a,b), при чем j¢ (x)¹0 на (a,b), то отношение конечных приращений этих функций на отрезке [a,b] равно отношению их производных в некоторой точке, которая может быть не единственной:
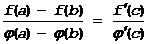
j (b)¹j(a) т.к. j¢(x) ¹0 на (a,b) Û т.Ролля.
Доказательство. Введем вспомогательную F(x)=f(x)-l×j(x),где l =const. Выберем теперь l такое, чтобы F(x) удовлетворяла условиям теоремы Ролля. Достаточно потребовать, чтобы F(a)=F(b). Другими словами:
F(a) -l×j (a)=f(b)- l×j (b) Þ
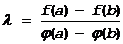 -конечное значение, т.к. j(b)¹j(a)
-конечное значение, т.к. j(b)¹j(a)
Тогда хотя бы в одной точке cÎ(a,b) F¢(c)=0 Þ 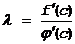 Þ
Þ
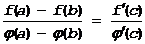
Теорема доказана.
Теорема Лагранжа (частный случай теоремы Коши). Пусть f(x) непрерывна на [a,b] и дифференцируема в (a,b). Тогда конечное приращение f(x) на [a,b] равно произведению длины отрезка [a,b] на значение производной в некоторой внутренней точке (a,b):
f(a)-f(b)=f¢(c)×(b-a)
Полагая в теореме Коши j (x)=x получим: j (b)-j(a)=b-a, j¢(x)º1 Þ j¢(c)=1
Поэтому
(*) 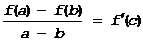 т.е.
т.е.
f(b)-f(a)=f¢(c)×(b-a)
Геометрический смысл теоремы Лагранжа определяется формулой ( * ). В ней левая часть есть угловой коэффициент хорды MN, соединяющей концы графической функции
РИСУНОК 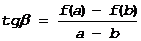
Правая часть формулы – угловой коэффициент в точке P с абсциссой x=cÎ(a,b)
f¢(c)=tg a Þ tg b=tg a, то есть хорда и касательная параллельны.
Таким образом, на произвольной дуге графика дифференцируемой функции всегда найдется хотя бы одна точка, в которой касательная будет параллельна хорде, стягивающей концы дуги.
Тот же геометрический смысл можно придать и теореме Коши, если рассматривать y=f(t) и x=j(t) как параметрические уравнения кривой в плоскости XOY, а x считать параметром этой кривой.
Правило Бернулли-Лопиталя.
Раскрытием неопределенности в математическом анализе называют нахождение предела 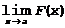 , когда f(x) непрерывна вблизи a, но не определена в самой этой точке, а непосредственная подстановка в функцию x=a приводит к выражению неопределенного вида
, когда f(x) непрерывна вблизи a, но не определена в самой этой точке, а непосредственная подстановка в функцию x=a приводит к выражению неопределенного вида
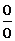 ,
, 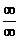 , 0×¥, ¥-¥, 1¥,0¥,¥0.
, 0×¥, ¥-¥, 1¥,0¥,¥0.
Опираясь на теорему Коши, выведем правило Бернулли-Лопиталя для раскрытия неопределенностей, используя производные.
Основными видами неопределенностей являются две:
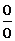 и
и 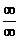 ,
,
раскрытие которых сводится к нахождению предела отношения двух бесконечно малых или бесконечно больших величин. Остальные виды сводятся к двум последним.
1. Рассмотрим неопределенность 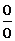 (при x®a), требуется найти
(при x®a), требуется найти 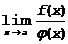 ,когда
,когда 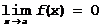 и
и 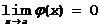 . Примем f(a)=j(a)=0. Тогда f(x) и j (x) будут непрерывными в x=a. Предположим также, что f(x) иj (x) дифференцируемы вблизи x=a причем j¢ (a)¹0. В этом случае:
. Примем f(a)=j(a)=0. Тогда f(x) и j (x) будут непрерывными в x=a. Предположим также, что f(x) иj (x) дифференцируемы вблизи x=a причем j¢ (a)¹0. В этом случае:
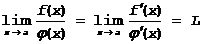 , (L - конечно или нет)
, (L - конечно или нет)
Доказательство. Применим к f(x) и j(x) теорему Коши на отрезке [x0,a),где x0Î окрестности a, в которой f и j непрерывны и дифференцируемы (может за исключением a). Тогда
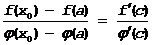
В силу того, что f(a)=j (a)=0 Þ
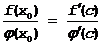 , где cÎ(x0,a)
, где cÎ(x0,a)
Если теперь x0®a, Þ и c®a, поэтому
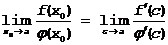
Теперь, если положить x0=x, c=x Þ
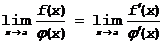
то есть в данном случае правило Бернулли-Лопиталя выполняется.
Примеры: 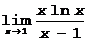
2. Неопределенность 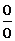 (x®¥). Докажем справедливость правила Бернулли-Лопиталя и в этом случае.
(x®¥). Докажем справедливость правила Бернулли-Лопиталя и в этом случае.
Итак требуется найти 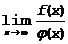 , если
, если 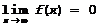 и
и 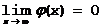 .
.
Предположим, что для достаточно больших x (|x|>M) обе функции дифференцируемы, j¢ (x)¹0 и что существует(конечный или бесконечный) 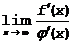 .
.
Докажем, что
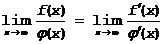
Доказательство. Перейдем к новому аргументу 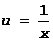 . Тогда, x®¥ Þ u®0. Нетрудно видеть, что к отношению
. Тогда, x®¥ Þ u®0. Нетрудно видеть, что к отношению 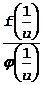 правило Бернулли-Лопиталя применимо: в окрестности u=0 f и j дифференцируемы, а
правило Бернулли-Лопиталя применимо: в окрестности u=0 f и j дифференцируемы, а 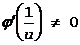 и существует
и существует
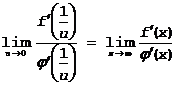
Тогда, принимая правило Бернулли-Лопиталя, получим
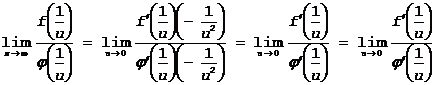
Возвращаясь к x, получим:
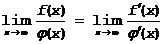
Правило остается в силе при x®+¥ или x®-¥.
Пример. 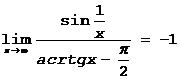 .
.
3. Неопределенность 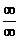 (x®a). Пусть теперь нужно найти
(x®a). Пусть теперь нужно найти 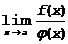 , если
, если 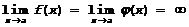 .
.
Как и в случае 1., пусть f и j дифференцируемы вблизи a, и j¢ (x)¹0.
Тогда, если существует (конечный или бесконечный) 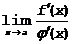 , то
, то
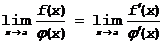
Доказательство. Пусть x1 и x2 Î окрестности x=a, и пусть x1<x2<a, если точки берутся слева от a, или x1>x2>a - если справа.Тогда на отрезке [x1,x2] или [x2,x1]) к отношению f(x) и j (x) применима теорема Коши:
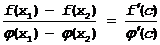 cÎ[ x1,x2 ]
cÎ[ x1,x2 ]
Далее пусть 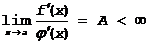
Зададим теперь e >0 и найдем d ( e )>0 такое, что при |x-a|< d ( e ) Þ
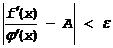 (*)
(*)
Выберем теперь x так, чтобы |x1-a|< d ( e ) и зафиксируем его. Тогда, согласно условию выбора x 2 Þ |x2-a|< d ( e ) и |c-a|< d ( e ), так как cÎ[ x1,x2 ]. Поэтому, в силу ( * ) будем иметь:
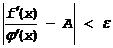 или
или 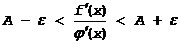
Заменяя в этом неравенстве отношение производных отношением конечных приращений функций, получим
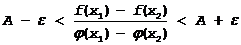 Þ
Þ
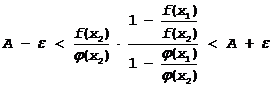 (1)
(1)
Если теперь x2®a, не изменяя x1, то, так как 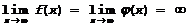 ,
,
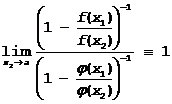
другими словами при заданном e, найдется d 1( e ), что при |x2-a|< d 1( e ) Þ
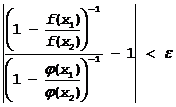 или
или
(1) 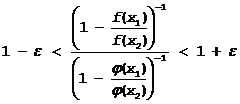
Перемножая теперь почленно неравенства (1) и (2) (что возможно, так как все члены неравенства (2) положительны), получим
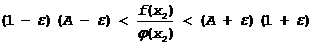
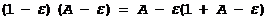 и
и 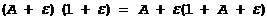
Другими словами разность между 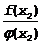 и постоянной A будет бесконечно малой величиной.
и постоянной A будет бесконечно малой величиной.
Следовательно 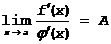 и следовательно
и следовательно
(3) 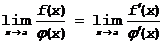
Пусть теперь 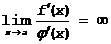 .Тогда f¢(x)¹0 в некоторой малой окрестности a (иначе
.Тогда f¢(x)¹0 в некоторой малой окрестности a (иначе 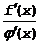 не было бы бесконечно большой величиной). С другой стороны
не было бы бесконечно большой величиной). С другой стороны 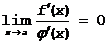 , а поэтому к обратному отношению применимо предыдущее правило:
, а поэтому к обратному отношению применимо предыдущее правило:
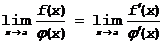
Из последней формулы вытекает справедливость и формулы (3).
Пример. 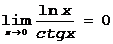
4. Неопределенность 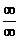 (x®¥). Правило применимо, если f(x) и j(x) дифференцируемы при любом x, |x|<M, причем j¢ (x)¹0 и при условии, что существует (конечный или бесконечный)
(x®¥). Правило применимо, если f(x) и j(x) дифференцируемы при любом x, |x|<M, причем j¢ (x)¹0 и при условии, что существует (конечный или бесконечный) 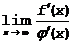 .
.
Для доказательства достаточно перейти к новому 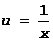 * и использовать правило для случая 3.
* и использовать правило для случая 3.
Пример. 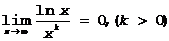 .
.
Правило Бернулли-Лопиталя иногда приходится применять несколько раз, если появляется неопределенность в отношении 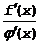 . Для этого необходимо соблюдение условий применимости теоремы Коши к производной
. Для этого необходимо соблюдение условий применимости теоремы Коши к производной
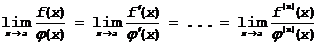 .
.
Примеры 1) 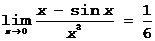 3 раза правило Бернулли-Лопиталя
3 раза правило Бернулли-Лопиталя
2) 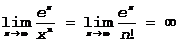 . n раз правило Бернулли-Лопиталя
. n раз правило Бернулли-Лопиталя
Примение правила Лопиталя к раскрытию неоределенности
0×¥, ¥-¥, 1¥,0¥,¥0 покажем на примерах. Идея- эти неопределенности сводятся в виду 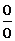 или
или 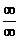 , а в последних 3-х случаях с применением логарифмирования.
, а в последних 3-х случаях с применением логарифмирования.
Пример 1. 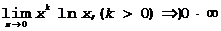
Представим в виде: 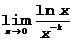 (xk – бесконечно малая величина, Þ
(xk – бесконечно малая величина, Þ 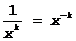 - бесконечно большая величина) Þ
- бесконечно большая величина) Þ 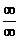 . x®0
. x®0
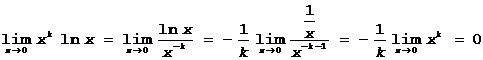
Пример 2. 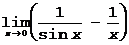 Þ ¥-¥, но
Þ ¥-¥, но
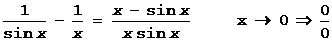 , применяя правило Лопиталя, получим:
, применяя правило Лопиталя, получим:
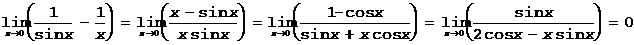
Пример 3.
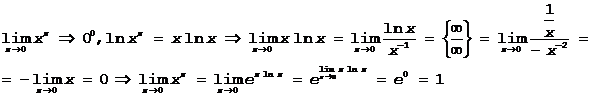 Пример 4.
Пример 4.
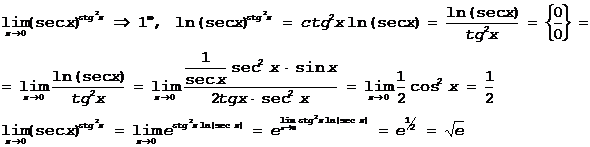
Правило Лопиталя не применимо, если не существует 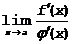 . Однако это еще не означает, что не существует
. Однако это еще не означает, что не существует 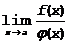 . Просто в этом случае правило Лопиталя нельзя использовать.
. Просто в этом случае правило Лопиталя нельзя использовать.
Пример. 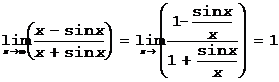 , тогда как
, тогда как 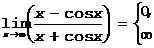 .
.
Признаки возрастания и убывания функций.
Определения возрастания и убывания функций было дано ранее.
Теорема 1) Если f(x), дифференцируемая на отрезке [a,b], возрастает на этом отрезке, то f¢(x) неотрицательна на [a,b], то есть
f¢(x)³0, "xÎ[a,b], если f(x),
2) Если f(x) непрерывна на [a,b] и дифференцируема в (a,b), причем f¢(x)>0, "xÎ(a,b), Þ f(x) возрастает на [a,b].
Доказательство .
1-я часть. Пусть f(x) на [a,b]. Придадим x приращение D x и рассмотрим
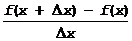 т.к. f(x) Þ
т.к. f(x) Þ
f(x+Dx)>f(x), если Dx>0
f(x+Dx)<f(x), если Dx<0
Но в обоих случаях
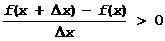 и следовательно
и следовательно
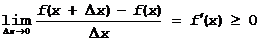 , что и следовало доказать.
, что и следовало доказать.
2-я часть. Пусть f¢(x)>0, " x(a,b). Рассмотрим x1 и x2, x1>x2, x1,x2Î[a,b]. По теореме Лагранжа f(x1)-f(x2)= (x1 - x2). По условию теоремы f¢(x)>0, x1-x2>0 и f(x1)-f(x2)>0 Þ f(x) возрастает.
Аналогично формулируется теорема для убывающей функции:
Теорема. Если f(x), дифференцируемая на отрезке [a,b], убывает на этом отрезке, то f¢(x)£0 на [a,b], то есть
f¢(x)£0, "xÎ[a,b], если
2) Если f(x) непрерывна на [a,b] и дифференцируема в (a,b), причем f¢(x)<0, "xÎ(a,b), Þ f(x) убывает на [a,b].
Геометрический смысл. Если f(x), касательная к кривой образует острый угол j с ОХ, или в некоторых точках угол j=0 Þ касательная параллельна оси ОХ, так как tgj³0. Если f(x)¯, угол j-тупой (или j=180о в отдельных точках Þ параллельна оси ОХ), так как tg j= f ¢(x)£ 0.
Таким образом, теоремы позволяют судить о возрастании или убывании функций по знаку производных.
Пример. Определение области возрастание и убывания функции y=x4
y¢=4×x3, x>0 Þ y¢>0, x<0 Þ y¢<0
Необходимое и достаточное условия существования экстремума функции.
Экстремальные значения f(x) и расположение точек экстремума характеризуют, в некотором смысле, изменение функции в зависимости от изменения аргумента. Определения даны в п….
Теорема 1. (Необходимое условие существования экстремума).
Если f(x) дифференцируема на (a,b) и при x=x1 имеет max или min (x1Î(a,b)), ее производная обращается в нуль в этой точке, то есть f¢(x1)=0. Эта теорема более слабая, чем теорема Ферма, так как требует дифференцируемости функции на (a,b), тогда как теорема Ферма – дифференцируемости только в точке x1.
Доказательство проводится аналогично: Пусть x1 -точка максимума, …
Замечание. Если f(x) определена на [a,b], то она может достигать max или min только на (a,b). Так как ее поведение при x<a или x>b неизвестно.
Геометрический смысл: в точках min и max касательная парллельнаОХ.
Следствие. Если f(x) дифференцируема при любом x, то она может иметь экстремумы только в тех точках, в которых ее производная обращается в нуль. Обратное же, вообще говоря, неверно. То есть max или min не обязательно достигаются в точках, в которых f¢(x)=0.
Например. y=x3, при x=0 имеет y¢=3x2, но при x>0 Þ y>0, а при x<0, то есть y<0,т.е. y=x3 в x=0 не имеет ни минимума, ни максимума.
Рассмотрим теперь случай, когда f(x) в некоторых точках не имеет производной. На примерах покажем, что в этих точках может быть max, min, или не быть ни того, ни другого.
1). Пусть y=|x|. Эта функция не имеет производной в точке x=0, но данная функция имеет в этой точке min Þ y=0 при x=0,а для любого x¹0 Þ y>0.
2). 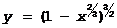 * не имеет производной при x=0, так как
* не имеет производной при x=0, так как 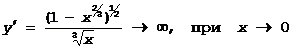
В x=0 функция имеет max: f(0)=1 и f(x)<1 при x¹0.
3). 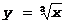 , при x=0 не имеет y¢ (
, при x=0 не имеет y¢ (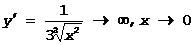 ), но в этой точке нет ни min, ни max, так как y(0)=0, x<0 Þ y<0 и x>0, y>0.
), но в этой точке нет ни min, ни max, так как y(0)=0, x<0 Þ y<0 и x>0, y>0.
Таким образом, функция может иметь экстремум лишь в 2-х случаях: либо в точках, где производная существует и равна 0, либо в точках, где f¢ не существует (терпит разрыв).
Определение. Значения аргумента, при которых f¢(x)=0, или f¢(x) терпит разрыв, называются критическими точками или критическими значениями.
Из выше сказанного следует, что не при всяком критическом значении f(x) достигает min или max, но те точки, в которых достигается экстремум-критические.
Для нахождения экстремумов находят все критические точки, а затем исследуют любые из них. Исследование функции в таких точках опирается на следующие теоремы:
Теорема 2. (Достаточные условия существования экстремума). Пусть f(x) непрерывна в некоторой окрестности критической точки x1 Î (a,b) и дифференцируема в этой окрестности, за исключением может быть самой x1. Если при переходе слева направо через производная меняет знак с + на -, то в x=x1 функция достигает максимального значения, если же с - на + -минимум f(x).
Таким образом, если
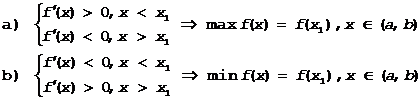
Доказательство. Пусть f¢(x) изменяет знак с + на -, то есть рассмотрим случай a). Применим теорему Лагранжа:
f(x)-f(x1)=f(x)(x-x1), где xÎ(x,x1)
1). Пусть далее x<x1. Þ x< x1, f¢(x)>0, f(x)(x-x1)<0 и следовательно f(x)-f(x1)<0 или f(x)<f(x1) (*)
2). x>x1. Þ x> x1, f¢(x)<0, f(x)(x-x1)<0 и следовательно f(x)-f(x1)<0 или f(x)<f(x1) (**)
Соотношения ( * ) и (* * ) показывают, что для любого x1 Î (a,b) f(x)<f(x1) Þ f(x1)=max f(x), x1 Î (a,b).
Аналогично доказывается вторая часть теоремы о достаточном условии минимума.
Геометрический смысл. Пусть x1 достигается max f(x) Þ x< x1, касательная к кривой образует острый угол a, а при x< x1, a - тупой. То есть до x1 f(x) возрастает, а после x1 f(x) убывает, таким образом в x1 происходит переход от возрастания к убыванию.
Аналогично для минимума Þ f(x) убывает до x1, а затем возрастает.
Если же f¢(x3)=0,но и для x< x3 и x< x3 f ¢(x) не изменяет знака Þ f(x) возрастает или убывает и до и после x3 и экстремум не достигается.
y=x3, y¢=3x2, y¢=f¢(x), при x=0, но при |x|>0 f¢(x)>0 -экстремума нет.
Дать рисунки для всех 3-х случаев.
Схема исследования дифференцируемой f(x) функции на экстремум с помощью первой производной.
1. Находится f¢(x).
2. Находятся критические x:
a) f¢(x)=0 и находятся действительные корни
Б) находятся x, при которых f¢(x) терпит разрыв.
3. Исследуется знак f¢(x) слева и справа от критической точки. Так как sign f¢(x)=const в интервале между критическими точками, то достаточно выбрать наиболее удобные для вычисления точки между критическими.
4. Вычисляются значения f(x) при любом критическом значении x.
В результате могут быть четыре возможных случая:
| x<x1 | x=x1 | x>x1 | |
| + | f¢(x1)=0 или разрыв | - | max |
| - | + | min | |
| + | + | f(x) | |
| - | - | f(x)¯ |
Примеры:
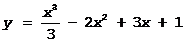
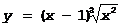
 2018-01-08
2018-01-08 1753
1753