2018-01-08
593
Согласно определению 
Естественно, что такой предел существует далеко не для всякой функции f(x) или не во всех точках области определения f(x).
Определение: Функция, имеющая в точке x=x0 производную, называется дифференцируемой в x0. Функция, имеющая производную во всех точках xÎ(a,b) называется дифференцируемой на (a,b).
Очевидно, что необходимым условием дифференцируемости функции в точке x0 или на (a,b) является ее непрерывность (в точке x0 или на (a,b)).
В самом деле 
существует тогда, когда Dy бесконечно малая одновременно с Dx. Докажем это утверждение:
Пусть y=f(x) - дифференцируема в x0 и y¢(x0)= y¢0. Это значит, что при x=x0, 
так как предел $ Þ 
(*),
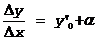где a - бесконечно малая величина.
Умножая (*) на D x получим D y=(y¢0+a)Dx,так как (y¢0+a) - ограниченная величина Þ D y - бесконечно малая величина и следовательно f(x) -непрерывна в x=x0.
Однако непрерывность f(x) не является достаточным условием дифференцируемости, так как для двух бесконечно малых величин предел их отношения может и не существовать (в частности равен ¥). Это означает, что не существует определенной касательной, или a=90 o и tga=¥. (Графические примеры).
Заключение: не всякая непрерывная функция дифференцируема, но всякая дифференцируемая функция непрерывна.
Определение. Дифференцируемая на (a,b) функция называется гладкой.
Определение. Функция f(x) называется дифференцируемой на отрезке [a,b],если она дифференцируема на интервале (a,b) и дифференцируема на концах отрезка в смысле существования правосторонней и левосторонней производной, то есть если существуют
и
Существует класс кусочно-гладких (дифференцируемых) и кусочно-непрерывных функций, для которых условия дифференцируемости (непрерывности) нарушаются в конечном числе изолированных точек.
В качестве примера нахождения производной рассмотрим дифференциацию функции y=xn, nÎN.
Производная от y=xn.
Исходя из определения, необходимо произвести следующие действия:
1) дать x приращение D x и вычислить значение f(x+Dx):
y+Dy=f(x+Dx)
2) найти Dy: Dy=f(x+Dx)-f(x)
3) составить отношение 
: 
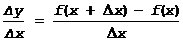
4) найти предел при D x®0:
Теорема. Производная от y=xn, где n>0 и nÎN,равна n×xn-1.
Доказательство. Итак
Далее мы покажем, что эта формула верна и для * дробного и отрицательного.
Примеры: y=x5, y¢=
y=x, y¢=
