Типы задач дискретного программирования

 

4.1.1. Основные понятия. Многие экономические задачи ха­рактеризуются тем, что объемы управляемых ресурсов (в силу тех или иных объективных свойств) могут принимать только целые значения. Математическая формализация данных ситуа­ций приводит к моделям дискретного программирования. В об­щем виде задача дискретного программирования может быть сформулирована как задача нахождения максимума (или мини­мума) целевой функции f (x ₁, x ₂, ...,x_n) на множестве D, опреде­ляемом системой ограничений

 

 

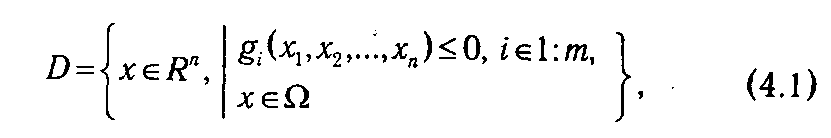
где Ω — некоторое конечное, или счетное*, множество. Ус­ловие х ∊Ω. называется условием дискретности. Особое место среди дискретных задач занимает целочисленная за­дача линейного программирования в канонической форме (ЦКЗЛП):

* Напомним, что примерами счетных множеств являются множества натуральных, целых и рациональных чисел.

 

 

где Z ⁺ ={0; 1; 2;...} — множество неотрицательных целых чи­сел.

Заметим, что в некоторых ситуациях требование «целочисленности» может быть наложено лишь на некоторые перемен­ные x_j, что кардинально не меняет характера задачи.

 

 

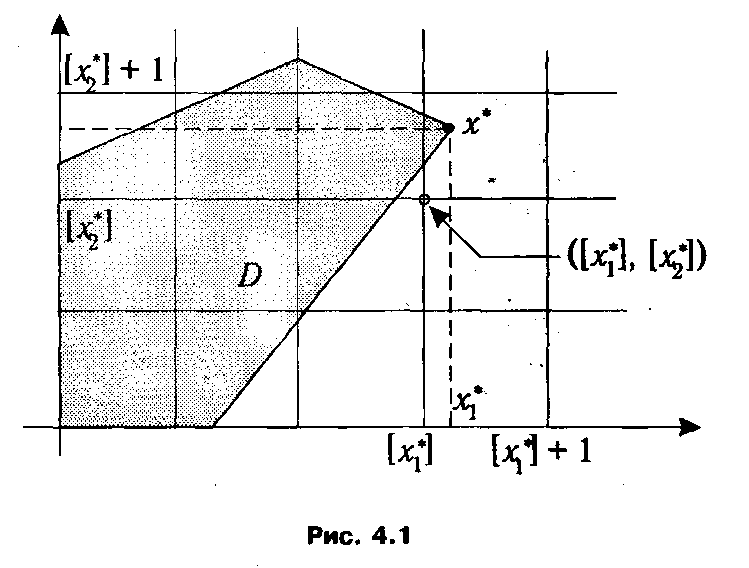
Принципиальная сложность, вызываемая наличием условий целочисленности в системе ограничений оптимизационной задачи, состоит в том, что в значительном количестве случаев невозможно заменить дискретную задачу ее непрерывным ана­логом и, найдя соответствующее решение, округлить его ком­поненты до ближайших целых значений. Пример, показанный на рис. 4.1, демонстрирует, что при округлении оптимального плана х* обычной задачи ЛП до целых значений получается точ­ка ([ х ₁*],[ x ₂^*]), не принадлежащая области допустимых планов задачи D. Условимся целую часть числа х_j. обозначать [ х_j ], а дробную — как { х_j }. Тогда х_j =[ х_j ]+{ х_j }. Отдельно следует до­бавить, что если даже оптимальный план непрерывной задачи, округленный до целых значений компонент, окажется допусти­мым, то целевая функция может вести себя так, что ее значение будет на нем существенно «хуже», чем на оптимальном плане целочисленной задачи.

Перечисленные проблемы предопределили необходимость разработки специальных методов решения дискретных и цело­численных задач. Но прежде чем говорить собственно о мето­дах решения, более подробно остановимся на классификации задач дискретного программирования. В литературе, как пра­вило, выделяют следующие классы дискретных оптимизацион­ных задач:

 

Ø Ø задачи с неделимостями;

Ø Ø экстремальные комбинаторные задачи;

Ø Ø задачи с разрывными целевыми функциями;

Ø Ø задачи на несвязных и невыпуклых областях и др.

 

4.1.2. Задачи с неделимостями. В подавляющем большин­стве случаев наличие условий неделимости определяется физи­ческими свойствами моделируемых объектов. Так, например, они могут появиться в качестве дополнительных ограничений в уже рассматривавшейся нами выше задаче производственного планирования, если в ней осуществляется управление выпуском крупной штучной продукции.

Классическим представителем задач данного класса стала так называемая задача о ранце. Ее фабула носит достаточно услов­ный характер и состоит в том, что солдат (или турист), собираю­щийся в поход, может нести груз весом не более W кг. Этот груз может состоять из набора предметов n типов, каждый предмет типа j весит w_j кг и характеризуется некоторой «полезностью» u_j, j ∊ 1: n. В рамках описанной ситуации вполне естественным представляется вопрос: сколько предметов каждого вида нужно положить в ранец, чтобы его суммарная полезность была макси­мальной? Если в качестве компонент плана х_j. принять количе­ство укладываемых предметов типа j, то данную задачу можно записать:

 

 

Как нетрудно заметить, представленная математическая мо­дель носит универсальный характер, и к ней могут быть сведены многие экономические задачи. Ярким подтверждением этому служит и тот факт, что в литературе она также известна как задача о загрузке судна.

4.1.3. Комбинаторные задачи. К данному классу относят­ся задачи оптимизации функции, заданной на конечном множе­стве, элементами которого служат выборки из n объектов.

Классическим представителем математических проблем та­кого рода стала задача о коммивояжере. Она состоит в состав­лении маршрута посещения торговым агентом, находящимся в некотором начальном пункте, n других городов при условии, что задана матрица стоимостей переездов из города в город

 

(с учетом начального). Причем допустимым является такой мар­шрут, который предусматривает однократное посещение всех городов и возвращение в исходный пункт. Очевидно, что наилучший маршрут должен минимизировать суммарную сто­имость переездов.

Планом задачи является маршрут коммивояжера, и его мож­но задать с помощью так называемой матрицы смежности

 

элементы которой определяются следующим образом:

 

1, если в маршруте предусмотрен переезд из пункта i в j,

x_i,j = 0, если в маршруте не предусмотрен переезд из пункта i в j,

 

причем по условию задачи x_ii =0, i ∊1: n.

Допустимыми планами служат связные маршруты, однознач­но определяемые упорядоченным набором посещаемых пунктов:

 

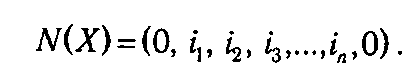
Каждый такой маршрут можно отождествить с перестанов­кой n чисел (упорядоченной выборкой из n элементов по n). В свою очередь, таким перестановкам взаимно однозначно со­ответствуют матрицы X, у которых в каждой строке и каждом столбце содержится точно одна единица.

С учетом сказанного задача коммивояжера принимает вид целочисленной задачи линейного программирования:

 

 

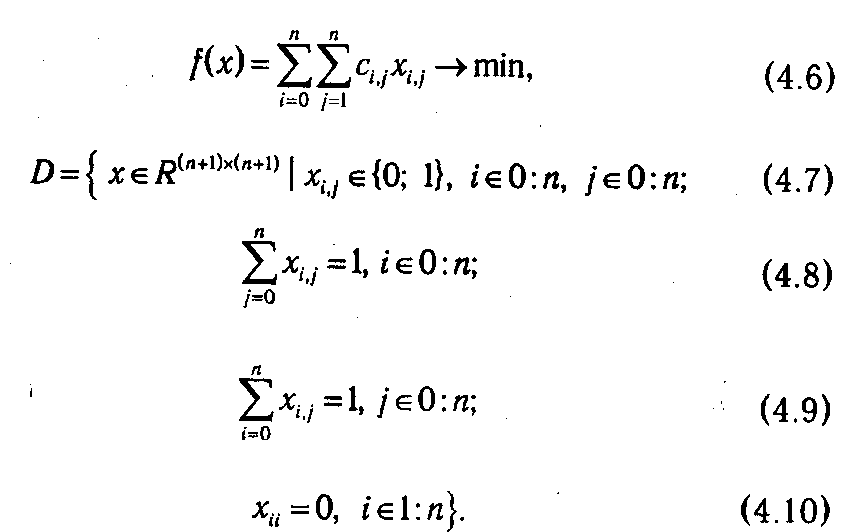
Условия (4.8) и (4.9) с содержательной точки зрения означа­ют, что в каждый пункт можно въехать и выехать только один раз. Приведенная форма записи задачи коммивояжера (4.6)-(4.10) не является самой рациональной и предназначена только для того, чтобы подчеркнуть ее общность с другими задачами дискретного программирования. Существует и другая форма, которая более ярко отражает комбинаторный характер данной проблемы:

 

 

где D — множество перестановок чисел от 1 до n.

Отдельно следует остановиться на том, что задача коммиво­яжера имеет большое количество содержательных аналогов. Скажем, к аналогичной модели приведет задача разработки графика переналадки оборудования, которое может выпускать разные типы изделий, но требует определенных затрат (времен­ных или материальных) при переходе с одного технологическо­го режима на другой.

4.1.4. Задачи с разрывными целевыми функциями. Как уже упоминалось выше, многие экономические системы ха­рактеризуются наличием так называемых постоянных затрат, которые должны быть произведены независимо от объема про­изводства. Учет в моделях этих и подобных факторов приводит к появлению в них целевых функций, не обладающих свойст­вом непрерывности. В качестве примера может быть приведена транспортная задача с фиксированными доплатами. Она отличается от транспортной задачи в матричной постановке, рассмотренной в главе 3, тем, что в ней затраты по перевозке груза из i -го пункта производства в j -й пункт потребления опре­деляются как

 

 

где с_i,j — по-прежнему издержки на перевозку единицы груза;

d_i,j — фиксированная доплата за аренду транспортных средств.

При таких предпосылках целевая функция суммарных затрат на перевозку

 

 

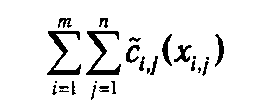
содержит «скачкообразные» разрывы, что существенно затруд­няет ее минимизацию, поэтому стандартный метод решения ос­нован на следующем преобразовании. Если ввести вспомога­тельные переменные у_i,j, такие, что

 

то целевая функция примет вид

 

 

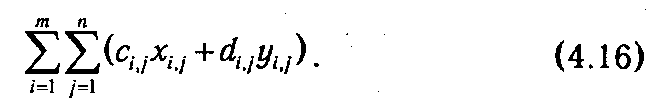
Действительно, если у_i,j =0, то переменные х_i,j =0, а при у_i,j =1 неравенства (4.15) становятся несущественными, поскольку они и так справедливы для любого опорного плана. Следова­тельно, задача (4.16) эквивалентна исходной задаче (4.13). В силу характера ограничений (4.14)-(4.15) задача (4.16) яв­ляется задачей частично-целочисленного программирования.

Перечисленные примеры далеко не исчерпывают всего мно­гообразия задач дискретного программирования. Однако более подробное их рассмотрение требует привлечения достаточно сложного математического аппарата и выходит за рамки дан­ной книги.

В последующих параграфах мы остановимся на способах ре­шения наиболее известных и хорошо изученных дискретных задач. Излагаемые ниже методы не имеют универсального ха­рактера, с каждым из них связаны определенные ограничения и, соответственно, ответ на вопрос о выборе того или иного из них зависит от конкретных особенностей решаемой задачи. Более того, цель изложения состоит в том, чтобы создать у читателя общие представления об основных идеях и подходах, не углубляясь далеко в вычислительные и математические тонкости, которыми буквально изобилуют алгоритмы дис­кретного программирования. Заметим также, что достаточно эффективный и широко применяемый подход к решению це­лочисленных задач основан на сведении их к задачам транс­портного типа. Это объясняется тем, что если в условиях транс­портной задачи значения запасов (а_i) и потребностей (b_j) являются целочисленными, то целочисленным будет и опти­мальный план.

МЕТОД ГОМОРИ

 

4.2.1. Основные идеи и принципы *. Данный метод, кото­рый также носит название метода отсекающих плоскостей, предназначен для решения ЦЗЛП в канонической форме (4.2)-(4.3). Кратко представим его основные идеи.

* Впервые был предложен Р.Гомори в 1957-1958 гг.

 

Отправной точкой для решения задачи (4.2)-(4.3) является решение ее непрерывного аналога, т. е. КЗЛП без учета условий целочисленности. Если получаемый в результате оптимальный план х* содержит только целые компоненты, то мы автомати­чески получаем и соответствующее решение ЦЗЛП. В против­ном случае к системе ограничений задачи должно быть добавле­но такое ограничение, для которого:

 

Ø Ø найденный нецелочисленный оптимальный план х * не удов­летворяет вновь добавляемому ограничению;

Ø Ø любой допустимый целочисленный план непрерывной задачи (4.2)-(4.3) удовлетворяет вновь добавляемому ограниче­нию.

 

Такое ограничение называют правильным отсечением. В первой геометрической интерпретации правильному отсече­нию соответствует гиперплоскость, отсекающая от выпуклого многогранного множества допустимых планов D некоторый мно­гогранник, не содержащий целочисленных планов.

Добавив сформированное отсекающее ограничение к уже су­ществующим, мы получаем новую оптимизационную задачу, после чего вычислительный процесс итеративно повторяется.

Теперь необходимо несколько более подробно остановиться на принципах формирования отсекающих ограничений. Вос­пользуемся системой обозначений, применявшихся при изло­жении вычислительных методов линейного программирования. Пусть β^{( q )} — оптимальный базис, полученный на последней итерации решения нецелочисленной ЗЛП. Если обозначить через α _i,j и ά _i коэффициенты матрицы задачи и вектора ограниче­ний в текущем базисе (A (β^{( q )}) и b (β^{( q )}))

 

 

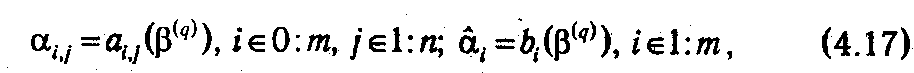
то i -ое уравнение в системе ограничений задачи примет вид:

 

 

Так как план x (β^{( q )}) является базисным, то в каждом уравнении все коэффициенты α _i,j, соответствующие базисным столбцам (j ∊ N (β^{( q )})), равны нулю за исключением некоторого α _i,ji =1, на основе чего из (4.18) получаем:

 

 

Если представить каждый коэффициент α _i,j в виде суммы це­лой и дробной частей α _i,j =[α _i,j ]+{α _i,j }, то получим

 

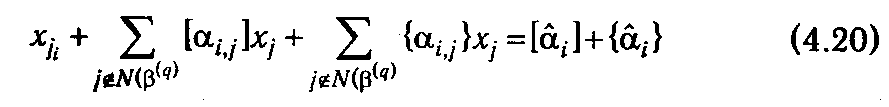
или

 

 

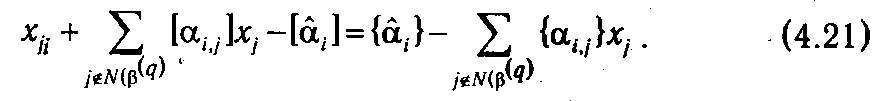
Из (4.21) следует, что если все х_j, j ∊1: n являются целыми, то целым будет и выражение

 

 

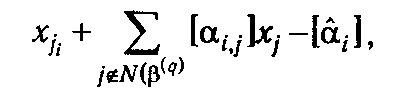
стоящее в левой части (4.21), и, стало быть, правая часть данно­го уравнения:

 

 

также должна быть целой. Предположим, что

 

 

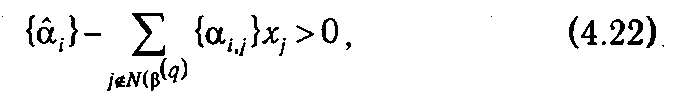
тогда, в силу того, что 0 ≤ {ά _i } < 1, а {α _i,j } ≥ 0, x_j ≥ 0, должно вы­полняться неравенство

 

 

Однако неравенства (4.22) и (4.23) противоречат требуемой целочисленности правой части (4.21) x_j (β^{( q )}). Следовательно, для целочисленных решений должно выполняться условие, проти­воположное неравенству (4.22), или, что то же самое,

 

 

В то же время (4.24) не выполняется для любого нецелочислен­ного базисного плана х. Действительно, небазисные компонен­ты плана равны нулю: х_j =0, j ∊ N (β^{( q )}), и (4.24) приобретает вид {ά _i } ≤0 <=> {ά _i } =0, но это противоречит предположению о нецелочисленности плана х, т. к. в базисном плане х_i = ά _i. Все сказанное позволяет утверждать, что ограничение (4.24) задает правильное отсечение.

Таким образом, с точки зрения организации техники, вычис­лений для осуществления правильного отсечения мы должны к системе ограничений нецелочисленной линейной задачи, реша­емой на q -й итерации, добавить условие

 

 

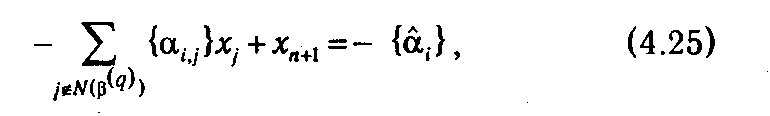
где x_{n +1} ≥0 — фиктивная переменная, добавляемая для преоб­разования неравенства в строгое равенство. Ей соответствует нулевой коэффициент в целевой функции.

Данному преобразованию условий задачи будет соответ­ствовать преобразование симплекс-таблицы, показанное на рис. 4.2. На нем по соображениям обеспечения наглядности ис­пользованы обозначения (4.17) и предполагается, что текущий базис β^{( q )} состоит из первых m столбцов.

 

 

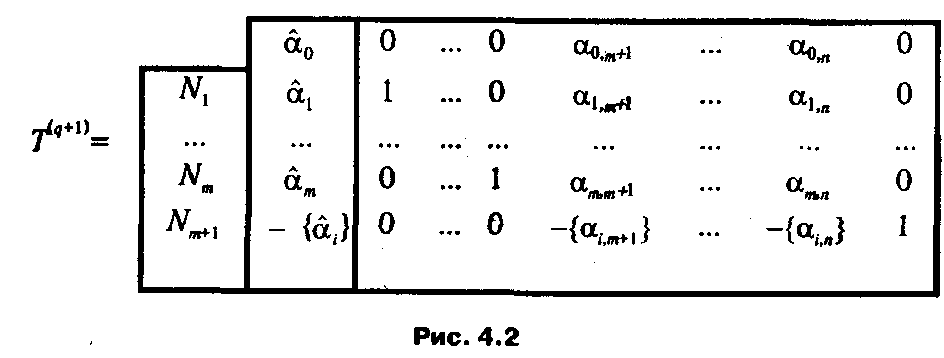
Индекс i соответствует выбранной для формирования отсе­чения строке симплекс-таблицы, содержащей нецелочисленное значение b_i (β^{( q )}).

Как видно из рис. 4.2, технически преобразование таблицы сводится к дописыванию одной строки и одного столбца. При этом легко убедиться, что модифицированные столбцы

 

совместно с добавленным столбцом

 

 

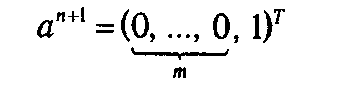
образуют сопряженный (двойственно допустимый) базис для сформированной задачи, а (ά₁,..., ά _m, -{ά _i }) являются ненуле­выми компонентами соответствующего псевдоплана. Исходя из этого, приходим к тому, что для решения вновь получен­ной задачи может быть эффективно применена процедура двойственного симплекс-метода (см. параграф 1.7).

Поскольку в начальном псевдоплане имеется только одна от­рицательная компонента (-{ά _i }), то из базиса должен быть вы­веден соответствующий ей вектор а^{n +1}. Далее, следуя рекомен­дациям алгоритма двойственного симплекс-метода, находим оптимальный план. Если он не является целочисленным, то опи­санные действия итеративно повторяются.

Если в ходе решения дополнительная переменная х_{n +1} вновь становится базисной, ее значение оказывается безразличным для основных переменных. Поэтому строку и столбец, отвеча­ющие ей, вычеркивают. С геометрической точки зрения это можно обосновать так: если псевдоплан оказывается внутри полупространства х_{n +1} ≥0, то дополнительное ограничение, оп­ределяемое гиперплоскостью х_{n +1}=0, становится несущест­венным и опускается.

4.2.2. Описание алгоритма. Приведем обобщенную схе­му алгоритма Гомори. Структурно он делится на так называе­мые большие итерации. Каждая большая итерация содержит этапы:

1. Решение «текущей» задачи методами линейного програм­мирования (малые итерации). На первой итерации в качестве «текущей» задачи выступает нецелочисленный аналог исходной ЦЗЛП.

2. Определение первой нецелочисленной компоненты в оп­тимальном плане, полученном на этапе 1. Если все компоненты являются целочисленными, то алгоритм завершается.

3. Построение для найденной компоненты условия отсече­ния согласно правилу (4.24), добавление сформированного ог­раничения к системе ограничений текущей задачи, т. е. форми­рование новой текущей задачи. Переход на начало следующей большой итерации.

Двойственный симплекс-метод является основой для метода Гомори, так как он позволяет учитывать новые дополнитель­ные ограничения (правильные отсечения) и переходить от те­кущего псевдоплана к новому оптимальному плану.

Можно доказать, что приведенный алгоритм конечен. Это означает, что на некотором шаге (итерации) будет найден цело­численный оптимальный план или обнаружен факт отсутствия допустимых целочисленных планов.

В качестве существенного замечания по поводу метода Гомори следует добавить, что при его практической реализации на ЭВМ следует считаться с ошибками округления, т, к. в усло­виях машинной арифметики практически ни один план не будет целочисленным. Кроме того, накапливающиеся погрешности могут внести возмущения в алгоритм и «увести» от оптимально­го целочисленного плана.

4.2.3. Пример решения ЦЗЛП методом Гомори. Рас­смотрим особенности применения метода Гомори на конкрет­ном примере. Пусть дана задача со следующими условиями:

 

 

Итерация 1. Используя обычный симплекс-алгоритм, реша­ем непрерывный аналог исходной задачи, в котором игнориру­ются условия целочисленности (4.28). В качестве исходного базиса можно взять первый и второй столбцы. На его основе заполняется таблица T ^(1,1) (первый индекс в обозначении табли­цы соответствует «большой» итерации, а второй — «малой»).

 

 

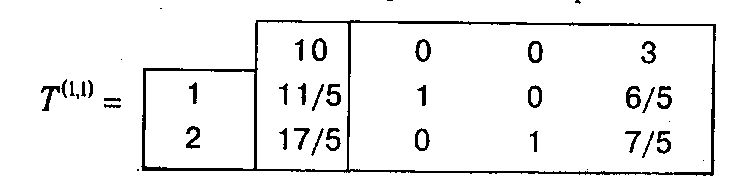
Как видно из строки оценок, данный базис является опти­мальным, однако соответствующий ему план х ={11/5,17/5, 0) не является целочисленным, поэтому выбираем из таблицы T ^(1,1) строку, содержащую первый нецелый элемент, и согласно формуле (4.25) строим отсекающее ограничение:

 

 

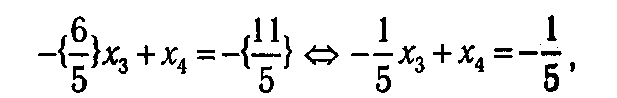
после чего переходим к следующей «большой» итерации.

Итерация 2. С учетом сформированного отсекающего ог­раничения заполняем симплекс-таблицу T ^(2,1).

 

 

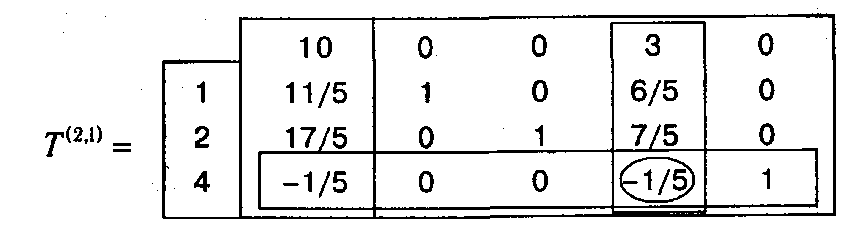
В соответствии с алгоритмом двойственного симплекс-мето­да переходим к следующему базису N (β^(2,2))={1, 2, 3}.

 

 

План, достигнутый в таблице T ^(2,2), является не только опти­мальным (b (β^(2,2))>0), но и полностью состоит из целочислен­ных компонент, т. е. решение задачи найдено: х * = (1, 2, 1) и f(x)= 7.