Динамического программирования

 

5.1.1. Основные идеи вычислительного метода динами­ческого программирования. Некоторые задачи математиче­ского программирования обладают специфическими особенно­стями, которые позволяют свести их решение к рассмотрению некоторого множества более простых «подзадач». В результа­те вопрос о глобальной оптимизации некоторой функции сводится к поэтапной оптимизации некоторых промежуточных целевых функций. В динамическом программировании* рас­сматриваются методы, позволяющие путем поэтапной (много­шаговой) оптимизации получить общий (результирующий) оп­тимум.

* Динамическое программирование как научное направление возник­ло и сформировалось в 1951-1953 гг. благодаря работам Р. Беллмана и его сотрудников.

 

Обычно методами динамического программирования опти­мизируют работу некоторых управляемых систем, эффект ко­торой оценивается аддитивной, или мультипликативной, целевой функцией. Аддитивной называется такая функция не­скольких переменных f (х ₁, x ₂, ...,х_n), значение которой вычис­ляется как сумма некоторых функций f_j, зависящих только от одной переменной х_j:

 

 

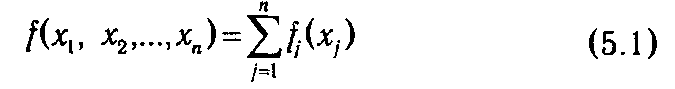
Слагаемые аддитивной целевой функции соответствуют эффек­ту решений, принимаемых на отдельных этапах управляемого процесса. По аналогии, мультипликативная функция распа­дается на произведение положительных функций различных пе­ременных:

 

 

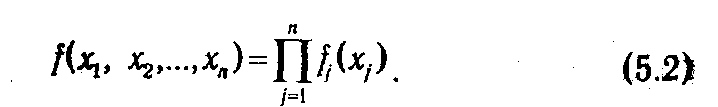
Поскольку логарифм функции типа (5.2) является аддитив­ной функцией, достаточно ограничиться рассмотрением функций вида (5.1).

Изложим сущность вычислительного метода динамическо­го программирования на примере задачи оптимизации

 

 

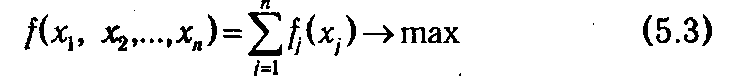
при ограниченияx

 

 

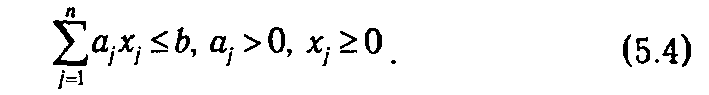
Отметим, что в отличие от задач, рассмотренных в преды­дущих главах, о линейности и дифференцируемости функций f_j (x_j) не делается никаких предположений, поэтому примене­ние классических методов оптимизации (например, метода Лагранжа) для решения задачи (5.3)-(5.4) либо проблематично, либо просто невозможно.

Содержательно задача (5.3)-(5.4) может быть интерпрети­рована как проблема оптимального вложения некоторых ресур­сов j, приводимых к единой размерности (например, денег) с помощью коэффициентов a_j, в различные активы (инвестици­онные проекты, предприятия и т. п.), характеризующиеся фун­кциями прибыли f_j, т. е. такого распределения ограниченного объема ресурса (b), которое максимизирует суммарную прибыль. Представим ситуацию, когда она решается последова­тельно для каждого актива. Если на первом шаге принято реше­ние о вложении в n -й актив x_n единиц, то на остальных шагах мы сможем распределить b-a_nx_n единиц ресурса. Абстрагируясь от соображений, на основе которых принималось решение на первом шаге (допустим, мы по каким-либо причинам не могли на него повлиять), будет вполне естественным поступить так, чтобы на оставшихся шагах распределение текущего объе­ма ресурса произошло оптимально, что равнозначно реше­нию задачи

 

 

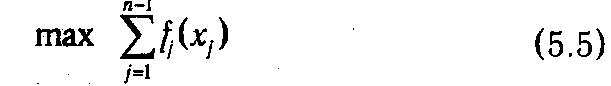
при ограничениях

 

 

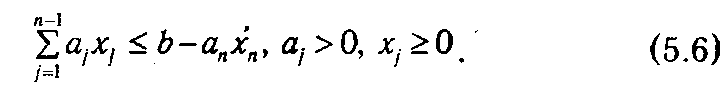
Очевидно, что максимальное значение (5.5) зависит от размера распределяемого остатка, и если оставшееся количество ресур­са обозначить через ξ, то величину (5.5) можно выразить как функцию от ξ:

 

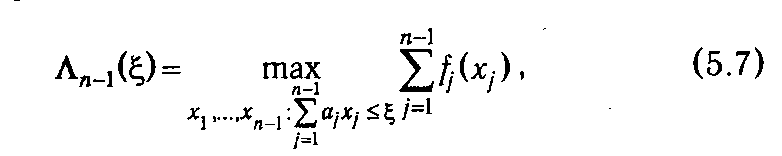
где индекс п -1 указывает на оставшееся количество шагов. Тогда суммарный доход, получаемый как следствие решения, принятого на первом шаге, и оптимальных решений, принятых на остальных шагах, будет

 

 

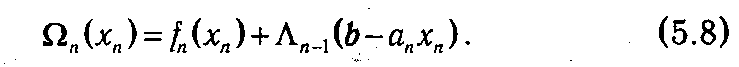
Если бы имелась возможность влиять на x_n , то мы для получе­ния максимальной прибыли должны были бы максимизировать Ω _n по переменной x_n, т. е. найти Λ _n (b) и фактически решить задачу:

 

 

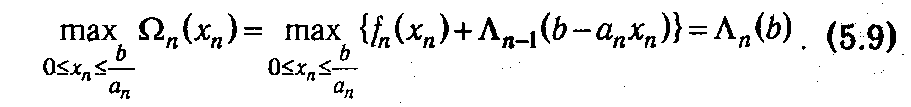
В результате мы получаем выражение для значения целевой функции задачи при оптимальном поэтапном процессе приня­тия решений о распределении ресурса. Оно в силу построения данного процесса равно глобальному оптимуму целевой фун­кции

 

 

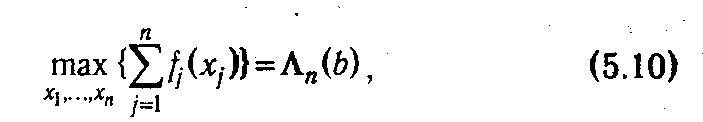
т. е. значению целевой функции при одномоментном распреде­лении ресурса.

Если в выражении (5.9) заменить значения b на ξ, и п на k, то его можно рассматривать как рекуррентную формулу, позво­ляющую последовательно вычислять оптимальные значения це­левой функции при распределении объема ресурса ξ за k шагов:

 

 

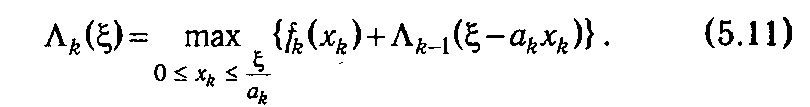
Значение переменной x_k, при котором достигается рассмат­риваемый максимум, обозначим 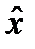_k (ξ).

При k = 1 формула (5.11) принимает вид

 

 

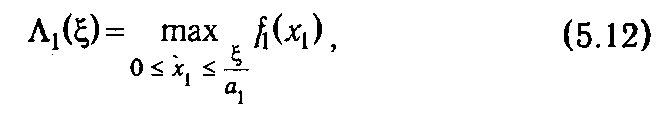
т. е. допускает непосредственное вычисление функций Λ₁(ξ) и 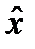₁(ξ).

Воспользовавшись (5.12) как базой рекурсии, можно с помо­щью (5.11) последовательно вычислить Λ _k (ξ) и 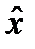_k (ξ), k ∊2: n. Положив на последнем шаге ξ = b, в силу (5.9), найдем глобаль­ный максимум функции (5.3), равный Λ _n (b), и компоненту опти­мального плана х_n* = 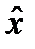_n (b). Полученная компонента позволяет вычислить нераспределенный остаток на следующем шаге при оптимальном планировании: ξ= b – а_nх*_n, и, в свою очередь, най­ти х*_{n- 1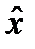}= _{n- 1}(ξ _{n- 1}). В результате подобных вычислений последо­вательно будут найдены все компоненты оптимального плана.

Таким образом, динамическое программирование представ­ляет собой целенаправленный перебор вариантов, который при­водит к нахождению глобального максимума. Уравнение (5.11), выражающее оптимальное решение на k -м шаге через решения, принятые на предыдущих шагах, называется основным рекур­рентным соотношением динамического программирова­ния. В то же время следует заметить, что описанная схема решения при столь общей постановке задачи имеет чисто тео­ретическое значение, так как замыкает вычислительный про­цесс на построение функций Λ _k (ξ) (k ∊1: n), т. е. сводит исход­ную задачу (5.3)—(5.4) к другой весьма сложной проблеме. Однако при определенных условиях применение рекуррентных соотношений может оказаться весьма плодотворным. В первую очередь это относится к задачам, которые допускают таблич­ное задание функций Λ _k (ξ).

5.1.2. Задачи динамического программирования, до­пускающие табличное задание рекуррентных соотноше­ний. Рассмотрим процесс решения модифицированного вариан­та задачи (5.3)-(5.4), в котором переменные х_j и параметры a_j, b могут принимать только целочисленные значения, а ограничение (5.4) имеет вид равенства. В рамках предложенной в п. 5.1.1 ин­терпретации о вложении средств в активы данные предпосылки вполне реалистичны и, более того, могут быть даже усилены тре­бованием о кратности значений х_j, например, 1000 единицам.

Чтобы не усложнять обозначения, условимся операции це­лочисленной арифметики записывать стандартным образом, по­лагая, что промежуточные результаты подвергаются правиль­ному округлению. Так, например, будем считать, что 12/5=2.

В соответствии с общей схемой вычислительного алгоритма на первом шаге мы должны построить функцию

 

 

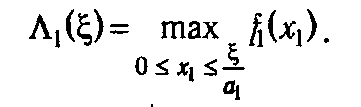
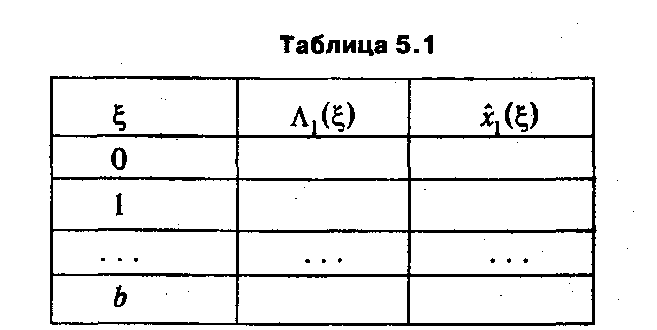
Поскольку ξ≤ b, x ₁ принимает конечное число целых значений от 0 до b / a ₁. Это позволяет, например, путем перебора значе­ний f ₁(x ₁) найти функцию Λ₁(ξ) и задать ее в форме таблицы следующей структуры (табл. 5.1).

Последняя колонка табл. 5.1 ( 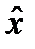₁(ξ)) содержит значение x ₁, на котором достигается оптимальное решение первого шага. Его необходимо запоминать для того, чтобы к последнему шагу иметь значения всех компонент оптимального плана.

На следующем (втором) шаге можно приступить к вычисле­нию функции Λ₂(ξ), значения которой для каждого отдельно взятого ξ∊ 0: b находятся как

 

 

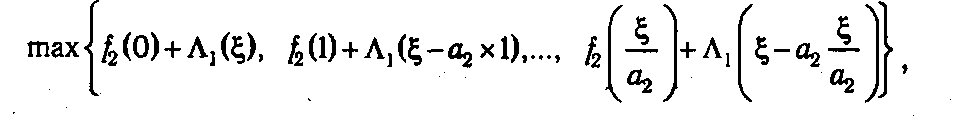
где значения

 

 

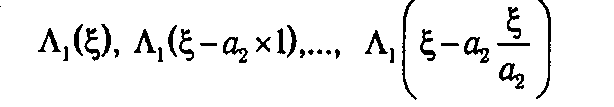
берутся из табл. 5.1. В результате вычислений формируется таблица значений Λ₂(ξ), содержащая на одну колонку больше по сравнению с табл. 5.1, так как теперь необходимо запомнить оптимальные решения первого ( 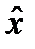₁(ξ)) и второго шагов ( ₂(ξ)).

 

 

На последующих шагах с номером k (k ∊2:(n-l)) осущест­вляются аналогичные действия, результатом которых стано­вятся таблицы значений Λ _k (ξ), где ξ ∊{0, 1,..., b } (см. табл. 5.2).

 

 

На последнем n -ом шаге нет необходимости табулиро­вать функцию Λ _n (ξ), так как достаточно определить лишь Λ _n (b) = f ( 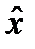_n (b)). Одновременно определяется и оптимальное значение n -й компоненты оптимального плана x*_n = 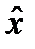_n (b). Далее, используя таблицу, сформированную на предыдущем шаге, определяем оптимальные значения остальных перемен­ных:

 

 

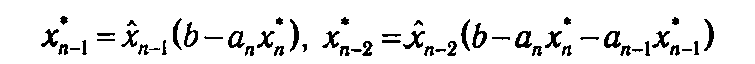
и т. д. или, в общем виде,

 

 

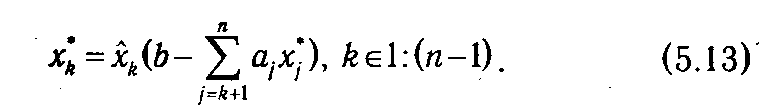
Подчеркнем одно из преимуществ описанного метода с точ­ки зрения его практической реализации в рамках программного обеспечения для ЭВМ: на каждом шаге алгоритма непосред­ственно используется только таблица, полученная на предыду­щем шаге, т. е. нет необходимости сохранять ранее полученные таблицы. Последнее позволяет существенно экономить ресур­сы компьютера.

Выигрыш, который дает применение рассмотренного алго­ритма, может также быть оценен с помощью следующего про­стого примера. Сравним приблизительно по числу операций (состоящих, в основном, из вычислений целевой функции) опи­санный метод с прямым перебором допустимых планов задачи (5.3)-(5.4) при а ₁ = a ₂ =... а_n = 1.

Количество допустимых планов такой задачи совпадает с ко­личеством целочисленных решений уравнения

 

 

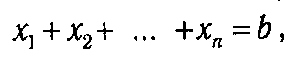
т. е. равно числу сочетаний с повторениями из n элементов по b. Следовательно, при простом переборе число возможных вари­антов составит

 

 

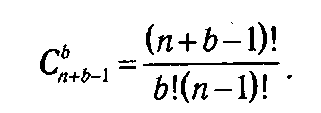
В случае применения метода динамического программирова­ния для вычисления таблицы значений функции Λ _k (ξ) при фик­сированном ξ необходимо выполнить (ξ+1) операций. Поэто­му для заполнения одной таблицы необходимо проделать

 

 

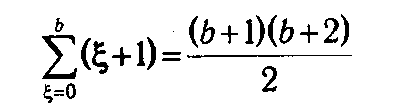
операций, из чего получаем, что для вычисления всех функции 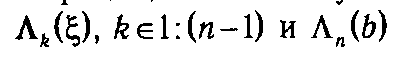потребуется

 

 

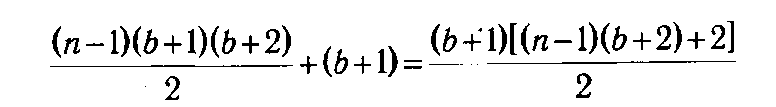
операций, что при больших n и b существенно меньше, чем в первом случае. Например, если п = 6 и b = 30, то непосредствен­ный перебор потребует выполнения 324 632 операций, а метод динамического программирования — только 2511.

5.1.3. Принцип оптимальности Беллмана. Еще раз под­черкнем, что смысл подхода, реализуемого в динамическом программировании, заключен в замене решения исходной мно­гомерной задачи последовательностью задач меньшей раз­мерности.

Перечислим основные требования к задачам, выполнение ко­торых позволяет применить данный подход:

 

Ø Ø объектом исследования должна служить управляемая сис­тема (объект) с заданными допустимыми состояниями и допустимыми управлениями;

 

Ø Ø задача должна позволять интерпретацию как многошаговый процесс, каждый шаг которого состоит из принятия реше­ния о выборе одного из допустимых управлений, приводя­щих к изменению состояния системы;

 

Ø Ø задача не должна зависеть от количества шагов и быть опре­деленной на каждом из них;

 

Ø Ø состояние системы на каждом шаге должно описываться оди­наковым (по составу) набором параметров;

 

Ø Ø последующее состояние, в котором оказывается система пос­ле выбора решения на k -м. шаге, зависит только от данного решения и исходного состояния к началу k -го шага. Данное свойство является основным с точки зрения идеологии дина­мического программирования и называется отсутствием последействия.

 

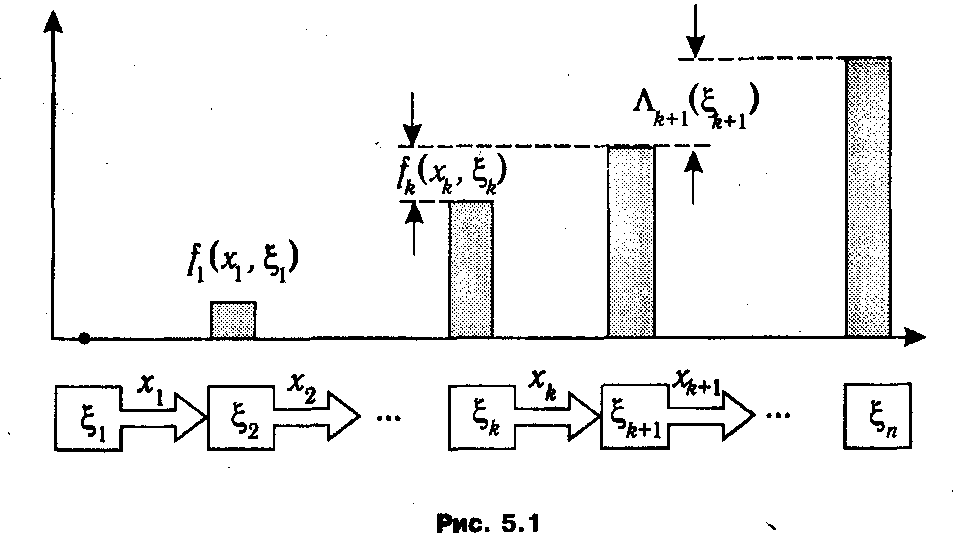
Рассмотрим вопросы применения модели динамического про­граммирования в обобщенном виде. Пусть стоит задача управ­ления некоторым абстрактным объектом, который может пре­бывать в различных состояниях. Текущее состояние объекта отождествляется с некоторым набором параметров, обознача­емым в дальнейшем ξ и именуемый вектором состояния. Пред­полагается, что задано множество Ξ всех возможных состоя­ний. Для объекта определено также множество допустимых управлений (управляющих воздействий) X, которое, не умаляя общности, можно считать числовым множеством. Управляю­щие воздействия могут осуществляться в дискретные моменты времени k (k ∊1: n), причем управленческое решение заключа­ется в выборе одного из управлений x_k ∊ Х. Планом задачи или стратегией управления называется вектор х = (х ₁, х ₂,.., x_{n -1}), компонентами которого служат управления, выбранные на каждом шаге процесса. Ввиду предполагаемого отсутствия последействия между каждыми двумя последователь­ными состояниями объекта ξ _k и ξ _{k +1} существует известная функциональная зависимость, включающая также выбранное управление: ξ _{k +1} = φ _k (x_k, ξ _k), k ∊1: п -1. Тем самым задание на­чального состояния объекта ξ₁∊Ξ и выбор плана х однозначно определяют траекторию поведения объекта, как это показа­но на рис. 5.1.

Эффективность управления на каждом шаге k зависит от текущего состояния ξ _k , выбранного управления x_k и количе­ственно оценивается с помощью функций f_k (х_k, ξ _k), являющих­ся слагаемыми аддитивной целевой функции, характеризую­щей общую эффективность управления объектом. (Отметим, что в определение функции f_k (х_k, ξ _k) включается область до­пустимых значений х_k, и эта область, как правило, зависит от текущего состояния ξ _k .) Оптимальное управление, при задан­ном начальном состоянии ξ₁, сводится к выбору такого опти­мального плана х*, при котором достигается максимум суммы значений f_k на соответствующей траектории.

Основной принцип динамического программирования заклю­чается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции f_k (х_k, ξ _k), а выбирать

 

 

оптимальное управление х_k* в предположении об оптимально­сти всех последующих шагов. Формально указанный принцип реализуется путем отыскания на каждом шаге k условных оптимальных управлений 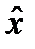_k (ξ), ξ∊Ξ, обеспечивающих наи­большую суммарную эффективность начиная с этого шага, в предположении, что текущим является состояние ξ.

Обозначим Λ _k (ξ) максимальное значение суммы функций f_k на протяжении шагов от k до п (получаемое при оптимальном управлении на данном отрезке процесса), при условии, что объект в начале шага k находится в состоянии ξ. Тогда функции Λ _k (ξ) должны удовлетворять рекуррентному соотношению:

 

 

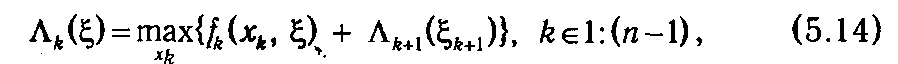
где ξ _{k +1} = φ _k (x_k, ξ)

 

Соотношение (5.14) называют основным рекуррентным со­отношением динамического программирования. Оно реализу­ет базовый принцип динамического программирования, извест­ный также как принцип оптимальности Беллмана:

 

F Оптимальная стратегия управления должна удовлетворять следующему условию: каково бы ни было

начальное состо­яние ξ _k на k-м шаге и выбранное на этом шаге управле­ние х_k,, последующие управления (управленческие реше­ния) должны быть оптимальными по отношению к состоянию ξ _{k +1} = φ _k (x_k, ξ _k), получающемуся в результа­те решения, принятого на шаге k.

 

Основное соотношение (5.14) позволяет найти функции Λ _k (ξ) только в сочетании с начальным условием, каковым в нашем случае является равенство

 

 

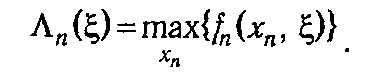
Сравнение рекуррентной формулы (5.14) с аналогичными соотношениями в рассмотренных выше примерах указывает на их внешнее различие. Это различие обусловлено тем, что в за­даче распределения ресурсов фиксированным является конечное состояние управляемого процесса. Поэтому принцип Бел­лмана применяется не к последующим, а к начальным этапам управления, и начальное соотношение имеет вид

 

 

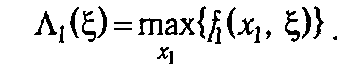
Важно еще раз подчеркнуть, что сформулированный выше принцип оптимальности применим только для управления объектами, у которых выбор оптимального управления не зави­сит от предыстории управляемого процесса, т. е. от того, каким путем система пришла в текущее состояние. Именно это обсто­ятельство позволяет осуществить декомпозицию задачи и сде­лать возможным ее практическое решение.

В то же время, говоря о динамическом программировании как о методе решения оптимизационных задач, необходимо отметить и его слабые стороны. Так, в предложенной схеме решения зада­чи (5.3)-(5.4) существенным образом используется тот факт, что система ограничений содержит только одно неравенство, и, как следствие, ее состояние задается одним числом — нераспре­деленным ресурсом ξ. При наличии нескольких ограничений со­стояние управляемого объекта на каждом шаге характеризуется уже набором параметров ξ₁, ξ₂,..., ξ _m, и табулировать значения функций Λ _k (ξ₁, ξ₂,..., ξ _m) необходимо для многократно больше­го количества точек. Последнее обстоятельство делает приме­нение метода динамического программирования явно нерацио­нальным или даже просто невозможным. Данную проблему его основоположник Р. Беллман эффектно назвал «проклятием многомерности». В настоящее время разработаны определенные пути преодоления указанных трудностей. Подробную информа­цию о них можно найти в специальной литературе [4, 5].