Метод ветвей и границ

 

4.3.1. Общая схема метода «ветвей и границ». Другим широко применяемым для решения задач дискретного програм­мирования методом является метод ветвей и границ. Впервые данный метод для решения ЦЗЛП предложили в 1960 г. Лэнг и Дойг, а его «второе рождение» произошло в 1963 г. в связи с выходом работы Литтла, Мурти, Суини и Кэрел, посвященной решению задачи о коммивояжере [33].

Вообще говоря, термин «метод ветвей и границ» является соби­рательным и включает в себе целое семейство методов, применяе­мых для решения как линейных, так и нелинейных дискретных задач, объединяемое общими принципами. Кратко изложим их.

Пусть стоит задача:

 

 

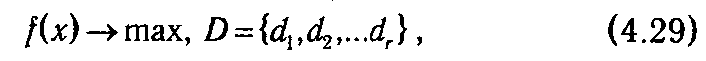
где D — конечное множество.

Алгоритм является итеративным, и на каждой итерации про­исходит работа с некоторым подмножеством множества D. На­зовем это подмножество текущим и будем обозначать его как D ^{( q )}, где q — индекс итерации. Перед началом первой итерации в качестве текущего множества выбирается все множество D (D ⁽¹⁾ =D), и для него некоторым способом вычисляется значе­ние верхней оценки для целевой функции max f(x) ≤ ξ(D ⁽¹⁾). Стандартная итерация алгоритма состоит из следующих этапов:

1°. Если можно указать план x ^(q)∊ D ^(q), для которого f(x ^(q) ) ≤ξ(D ^(q)), то x ^(q)= х* — решение задачи (4.29).

2°. Если такой план не найден, то область определения D ^(q) некоторым образом разбивается на подмножества D ₁^(q), D ₂^(q),..., D_lq ^(q), удовлетворяющие условиям:

 

 

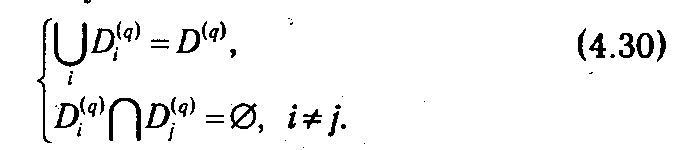
Для каждого подмножества находятся оценки сверху (вер­хние границы) для целевой функции ξ D ₁^{( q )}, ξ D ₂^{( q )},..., ξ D_{l 1}^{( q )}, уточняющие ранее полученную оценку ξ D ^{( q )}, то есть ξ D_i ^{( q )} ≤ ξ D ^{( q )}, i ∊1: l_q. Возможно одно из двух:

2.1. Если существует такой план х ^{( q )}, что

 

 

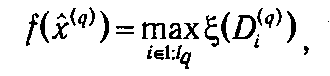
то этот план оптимальный.

 

 

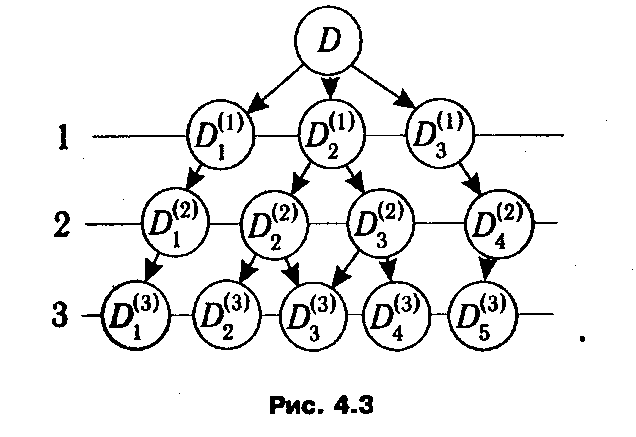
2.2. Если такой план не найден, то выбирается одно из мно­жеств D_i ^{( q )}, i ∊1: l_q (как правило, имеющее наибольшую оценку

 

 

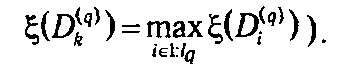
Все имеющиеся к текущему моменту концевые подмножества, т. е. те подмножества, которые еще не подверглись процессу дробления, переобозначаются как D ₁^{( q +1)}, D ₂^{( q +1)},..., D_{l ( q +1)}^{( q +1)}, после чего процесс повторяется.

Схема дробления множества D представлена на рис. 4.3 в виде графа. Существуют и более сложные системы индексации подмножеств, при которых не требуется их переобозначение на каждом шаге.

Конкретные реализации метода ветвей и границ связаны с правилами разбиения на подмножества (правилами ветвления) и построения оценок значений целевых функций на данных под­множествах (границ).

4.3.2. Решение ЦЗЛП методом ветвей и границ. Рас­смотрим применение алгоритма метода ветвей и границ для решения ЦЗЛП (4.2)-(4.3). Как уже упоминалось, через D ^{( q )} обозначается подмножество множества допустимых планов за­дачи. Перед началом первой итерации (q = 1) в качестве теку­щего множества берется все множество D (D ⁽¹⁾ = D), после чего решается стандартная задача линейного программирования (D ⁽¹⁾, f). Нетрудно заметить, что она является непрерывным аналогом

 

 

исходной задачи (4.2)-(4.3). Если найденный оптималь­ный план 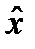⁽¹⁾ содержит только целочисленные компоненты, то он является и оптимальным планом для (4.2)-(4.3): 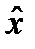⁽¹⁾ = x*. В противном случае значение f ( 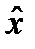⁽¹⁾) становится оценкой (верх­ней границей) значения целевой функции на множестве D ⁽¹⁾, и мы переходим к выполнению стандартной итерации алгоритма. Опишем входящие в нее этапы.

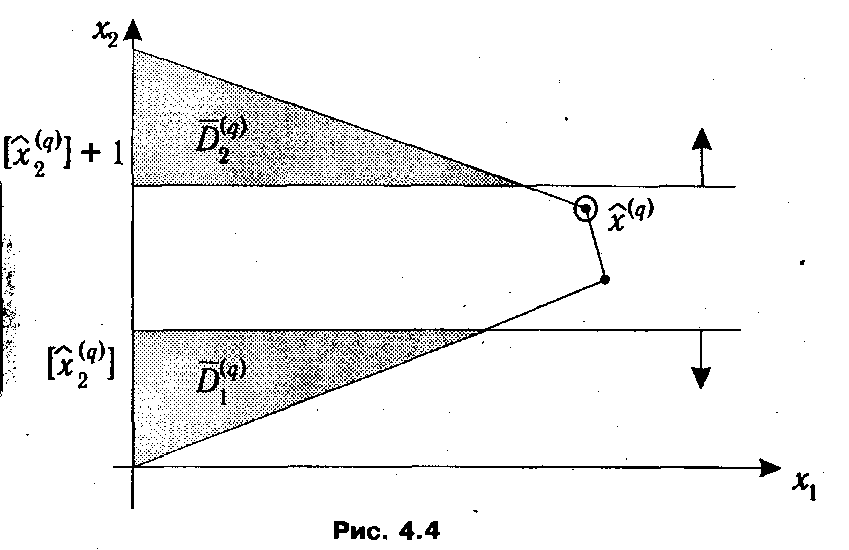
1) Выбирается некоторая нецелочисленная компонента пла­на 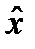_k ^{( q )}. Поскольку в оптимальном плане она должна быть це­лой, то можно наложить ограничения x_k ≤ [ 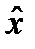_k ^{( q )}] и x_k ≥ [ 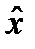_k ^{( q )}]+1. Таким образом, D ^{( q )} разбивается на подмножества

 

 

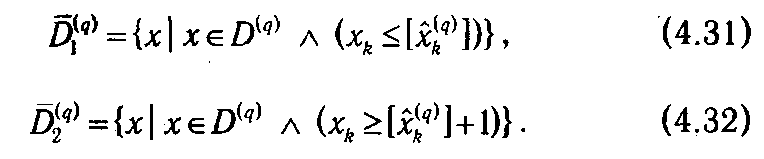
Графическая интерпретация такого разбиения множества D ^{( q )} приведена на рис. 4.4.

2) Решаются задачи линейного программирования

 

 

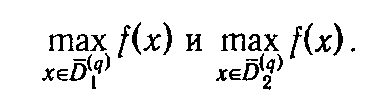
Соответствующие максимальные значения целевой функции принимаются как ее оценки на этих множествах:

 

 

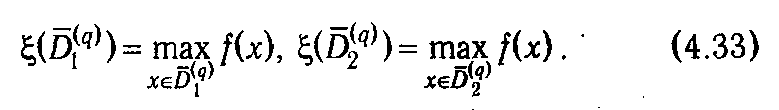
Если оптимальный план для одной из решенных задач удов­летворяет условию

 

 

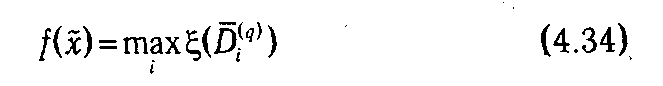
и содержит только целые компоненты, то, значит, найдено ре­шение основной задачи (4.2)-(4.3). В противном случае среди всех концевых подмножеств, полученных как на предыду­щих (D_i ^{( q )}), так и на текущем (D ₁^{( q )}, D ₂^{( q )}) этапе, выбирается об­ласть с наибольшей оценкой ξ(D_i ^{( q )}). Она становится текущим рассматриваемым подмножеством (D ^{( q +1)}). Далее производится перенумерация концевых множеств и вычислительный процесс итеративно повторяется.

При решении задач (D ₁^{( q )}, f) и (D ₂^{( q )}, f) можно воспользовать­ся результатами решения предыдущей задачи (D ^{( q )}, f). Рас­смотрим вариант организации вычислительного процесса на примере задачи ( ₁^{( q )}, f) (для ( ₂^{( q )}, f) он выглядит аналогично с точностью до знаков неравенств).

Предположим, что на последнем шаге решения задачи (D ^{( q )}, f) был получен оптимальный базис β. Без ограничения общности можно считать, что он состоит из первых m столбцов матрицы задачи. Данное предположение делается исключитель­но для обеспечения наглядности дальнейшего изложения и оче­видно, что его выполнения можно всегда добиться за счет про­стой перенумерации векторов а^j. По аналогии с предыдущим параграфом введем обозначения для элементов матрицы задачи (D ^{( q )}, f) и ее вектора ограничений относительно базиса :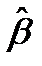

 

 

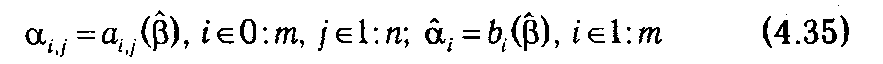
Тогда система ограничений задачи (D ^{( q )}, f) может быть пред­ставлена как

 

 

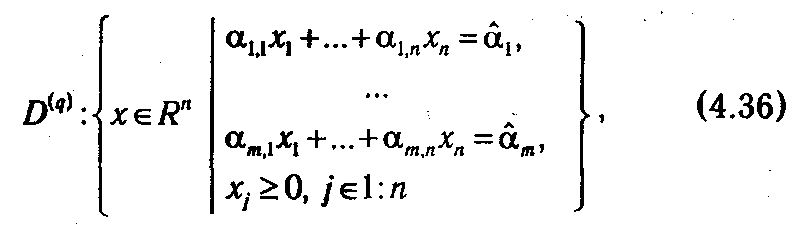
а получаемая на ее основе система ограничений задачи ( ₁^{( q )}, f) как

 

 

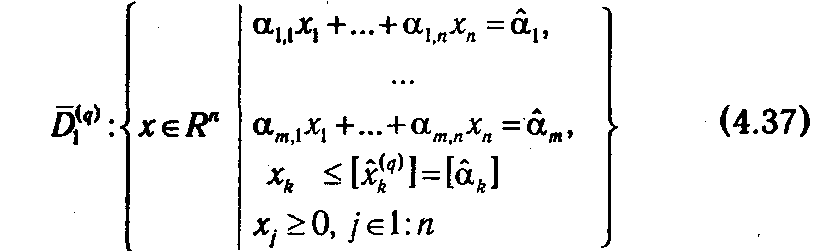
или

 

 

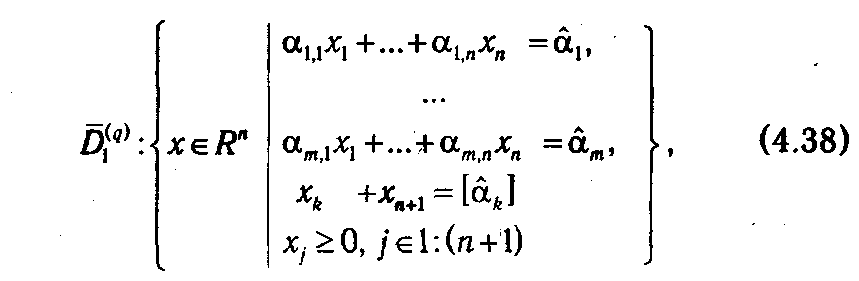
где х_{n +1} ≥ 0 — фиктивная переменная, которой соответствует нулевой коэффициент в целевой функции, добавляемая для пре­образования неравенства в строгое равенство.

Очевидно, что 1≤ k≤m, т. к. небазисные компоненты опти­мального плана (m +1≤ j≤n) равны нулю, т. е. являются заведо­мо целочисленными. Тогда с учетом сделанных предположений о виде базиса 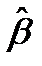можно записать:

 

 

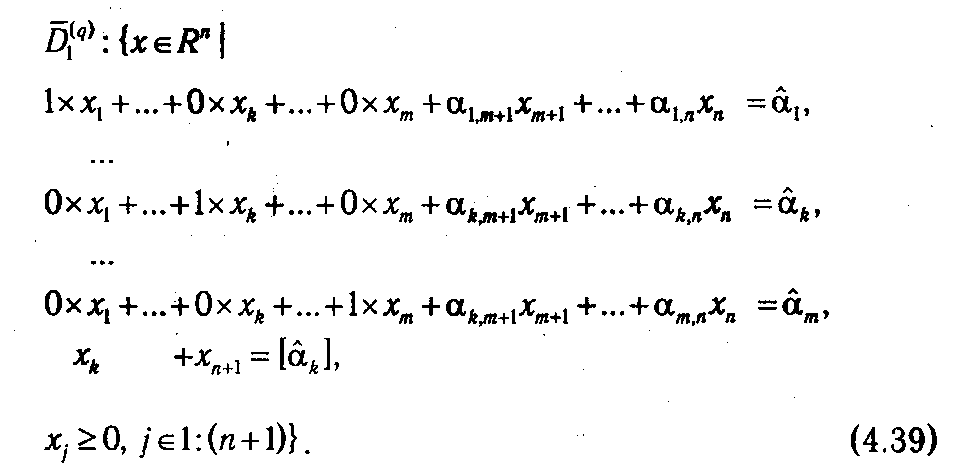
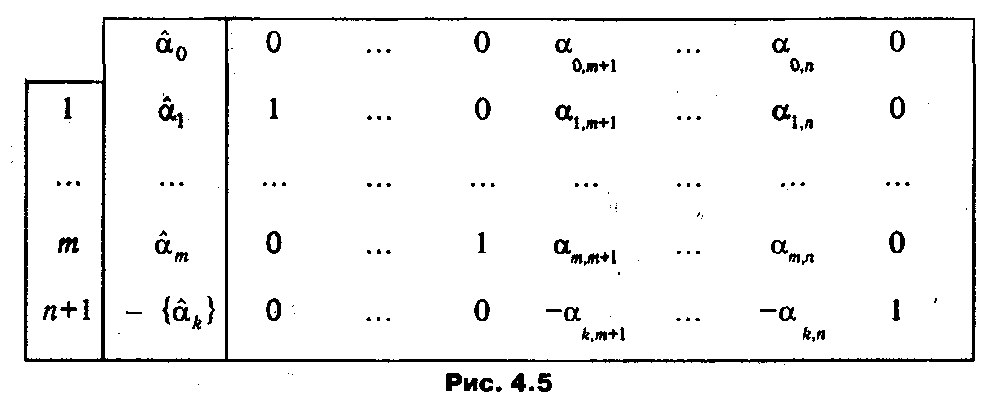
Как видно из (4.39), в k -м столбце имеется всего два отлич­ных от нуля элемента: в k -й и (m +1)-й строках. Если вычесть из (m +1)-го уравнения k -e, то, учитывая, что [ά _k ] – ά _k =-{ά _k }, по­лучим эквивалентную систему:

 

 

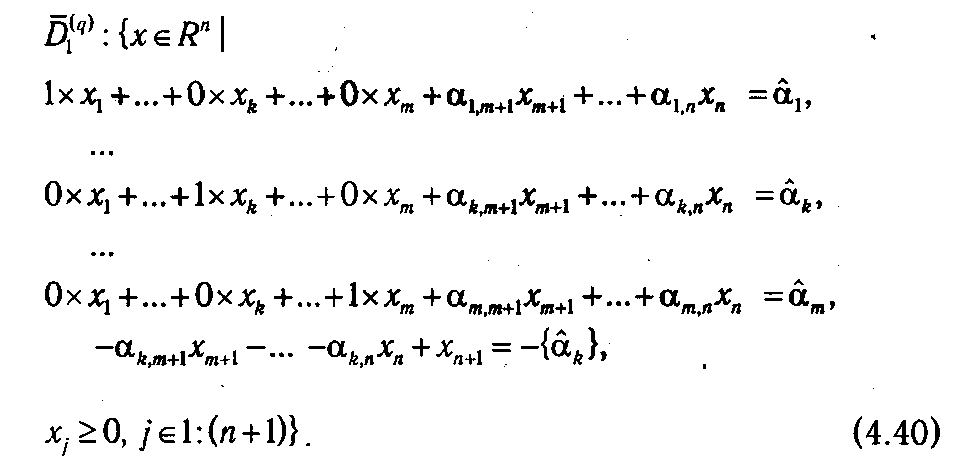
Проведенные преобразования системы ограничений D ₁^{( q )} по­зволили явно выделить сопряженный базис, образуемый столб­цами с номерами 1,..., m, n +1, и соответствующий ему псевдо­план (ά₁,..., ά _m, 0,...., 0, -{ά _k }), т.е. для решения задачи (D ₁^{( q )}, f) может быть применен алгоритм двойственного симплекс-мето­да. Практически вычислительный процесс для данного этапа сводится к преобразованию к симплекс-таблицы, показанному на рис. 4.5.

 

Для случая задачи (D ₂^{( q )}, f) преобразование симплекс-табли­цы, получаемое на базе аналогичных рассуждений, приведено на рис. 4.6.

 

 

Очевидным недостатком алгоритма метода ветвей и границ при решении задач большой размерности является необходи­мость перебрать слишком большое количество вариантов пе­ред тем, как будет найден оптимальный план. Однако он отчасти может быть преодолен, если ограничиться поиском не опти­мального, а просто «хорошего» (близкого к оптимальному) пла­на. О степени такой близости и скорости приближения к экст­ремуму нетрудно судить по изменению значений оценок.

Подчеркнем, что приведенная реализация метода ветвей и границ является одной из многих. Помимо нее, например, очень популярна версия метода решения задачи коммивояжера, в которой для ветвления и построения оценок используют специфические свойства данной модели. При желании о ней мож­но прочесть в [1, 14].

 

КЛЮЧЕВЫЕ ПОНЯТИЯ

 

Ø Ø Задачи с неделимостями.

Ø Ø Экстремальные комбинаторные задачи.

Ø Ø Задачи с разрывными целевыми функциями.

Ø Ø Правильное отсечение.

Ø Ø Метод Гомори.

Ø Ø Методы ветвей и границ.

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

4.1. Какие основные проблемы возникают при решении дис­кретных задач?

4.2. Сформулируйте задачу о ранце.

4.3. Какие экономико-математические модели могут быть све­дены к задаче о коммивояжере?

4.4. Приведите пример моделей с разрывными целевыми функ­циями.

4.5. Какой принцип используется для построения правильно­го отсечения в методе Гомори?

4.6. Перечислите основные этапы, входящие в «большую» итерацию метода Гомори.

4.7. Какую роль играет алгоритм двойственного симплекс-ме­тода при решении целочисленной

линейной задачи мето­дом Гомори?

4.8. Перечислите принципиальные идеи, лежащие в основе ме­тодов ветвей и границ.

4.9. Как производится построение отсечения при решении це­лочисленной линейной задачи методом

ветвей и границ?

4.10. Опишите схему решения целочисленной задачи линейно­го программирования методом ветвей и

границ.

4.11. За счет каких преобразований удается построить сопря­женный базис при добавлении

отсекающего ограничения?