Глава 6. Краткий обзор

ДРУГИХ РАЗДЕЛОВ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

 

Данная глава занимает особое положение среди остальных. Ее цель — представить читателю предельно краткую характерис­тику так называемых дополнительных разделов исследования операций. Поясним несколько смысл слова «дополнительный». Дело в том, что существуют различные подходы к классифика­ции этих научных отраслей: иногда их считают составными час­тями исследования операций, а иногда рассматривают как само­стоятельные дисциплины. Обе точки зрения имеют право на существование, но даже если придерживаться второй, разделы, о которых пойдет речь в настоящей главе, можно трактовать как смежные области знания, аппарат которых применим для решения задач исследования операций. Еще раз подчеркнем, что каждый параграф настоящей главы лишь обзорно затраги­вает общие вопросы соответствующих тем, а полные учебные курсы по ним существенно превышают объем данной книги.

ТЕОРИЯ ИГР

 

6.1.1. Предмет теории игры. Задачи, рассмотренные в пре­дыдущих главах, формулировались для ситуаций индивидуально­го выбора оптимальных решений, т.е. для случаев, когда решение принимает отдельно взятый субъект, обладающий единственной целью.

Принципиально иная ситуация возникает при изучении процессов принятия решений несколькими субъектами, инте­ресы которых могут не совпадать. При этом возникают задачи со многими целевыми функциями (критериями). Область мате­матики, изучающая данные проблемы, получила название тео­рии игр. Задачи теории игр относятся к области принятия ре­шений в условиях неопределенности, а их специфика состоит в том, что, как правило, подразумевается неопределенность, воз­никающая в результате действий двух или более «разумных» противников, способных оптимизировать свое поведение за счет других. Среди типичных примеров такого поведения могут быть названы действия конкурирующих фирм на одном рынке или планирование военных операций.

Одним из основных вопросов в задачах с коллективным вы­бором решений является вопрос об определении оптималь­ности, т. е. вопрос, какие решения следует признавать наилуч­шими в ситуации оптимизации по нескольким критериям, отражающим различные интересы. Многие методы решения проблем теории игр основываются на сведении их к задачам ма­тематического программирования. На наиболее простых из них мы остановимся в настоящей главе.

Теория игр берет начало от работ Э. Бореля (1921 г.), а прин­ципиальным этапом в ее становлении как самостоятельного на­учного направления стала монография Дж. Неймана, вышед­шая в 1944 г. [25].

6.1.2. Терминология и классификация игр. Особенно­стью теории игр как научной дисциплины стала употребляемая в ней специфическая терминология. Термин «игра» применяется для обозначения совокупности правил и соглашений, которыми руководствуются субъекты, поведение которых мы изучаем. Каждый такой субъект k, где k ∊l: K, или игрок, характеризует­ся наличием индивидуальной системы целевых установок и стра­тегий s ₁ ^k, s ₂ ^k,..., s_mk^k, т. е. возможных вариантов действий в игре.

Достаточно распространенный способ математического описания игры основан на задании функций f_k (s ¹ _{i 1} , s ² _{i 2} ,..., s^k_ik ,..., s^K_ik), каждая из которых определяет результат (платеж, выигрыш), получаемый k -м игроком в зависимости от набора стратегий S =(s ¹ _{i 1} , s ² _{i 2} ,..., s^k_ik ,..., s^K_ik), примененного всеми участ­никами игры. Функции f_k, k ∊l: K также называют функциями выигрыша, или платежными функциями. В том случае, если для любых S

 

 

игра называется игрой с нулевой суммой. Игру с двумя участ­никами и нулевой суммой называют антагонистической. Ан­тагонистические игры, т. е. игры, в которых выигрыш одного участника равен проигрышу другого, в силу относительно про­стой постановки задачи являются наиболее изученным разде­лом теории игр. Однако содержание теории игр, безусловно, не исчерпывается ими. В классификации игровых моделей вы­деляют игры с конечными и бесконечными наборами стратегий у игроков, выделяют игры по возможным количествам ходов у участников. Также игры делят на некооперативные и коопе­ративные, т. е. те, в которых функции выигрыша участников зависят от образуемых ими коалиций. Помимо этого игры мож­но различать по объему информации, имеющейся у игроков от­носительно прошлых ходов. В этой связи они делятся на игры с полной и неполной информацией. Заинтересованный читатель может обратиться к таким источникам, как [17, 23].

6.1.3. Матричные игры и понятие седловой точки. Рас­смотрим более подробно антагонистические игры и их основ­ные свойства. Удобным способом задания игры двух участников с нулевой суммой является платежная матрица. Отсюда, кстати, происходит еще одно их название — матричные игры. Каждый элемент платежной матрицы а_ij содержит числовое значение выигрыша игрока I (проигрыша игрока II), если пер­вый применяет стратегию i, а второй — стратегию j. Термины выигрыш и проигрыш следует понимать в широком смысле, т. к. они могут принимать отрицательные значения и с житейской точки зрения означать противоположное. Нетривиальность за­дачи прежде всего заключается в том, что каждый из игроков делает свой выбор, не зная о выборе другого, что существенно осложняет процесс оптимизации выбираемой стратегии.

Классическим примером антагонистической игры является игра с двумя участниками, загадывающими независимо друг от друга числа. Предполагается, что если их сумма оказывается чет­ной, то выигрыш, равный 1, достается первому игроку, а если не­четной, то второму. Положив, что для обоих игроков загадыва­ние нечетного числа является первой стратегией, а четного — второй, можем записать платежную матрицу данной игры:

 

 

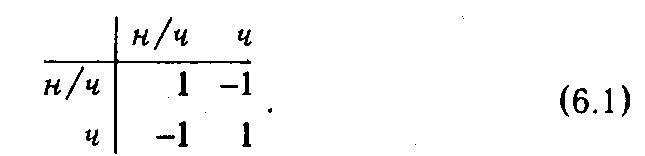
Строки матрицы (6.1) соответствуют стратегиям игрока I, столб­цы — стратегиям игрока II, а ее элементы — результатам перво­го игрока. Также из определения игры следует, что элементы данной матрицы, взятые с обратным знаком, соответствуют вы­игрышам второго игрока.

Более сложная и содержательная платежная матрица может быть получена, если несколько модифицировать предложен­ную игру. Допустим, что оба участника имеют право загадывать числа от 1 до 4, что составляет их соответствующие стратегии. В случае, если результат сложения задуманных чисел будет четным, то второй игрок выплачивает первому получившуюся сумму, а если нечетным, то первый — второму. Запишем пла­тежную матрицу для такой игры:

 

 

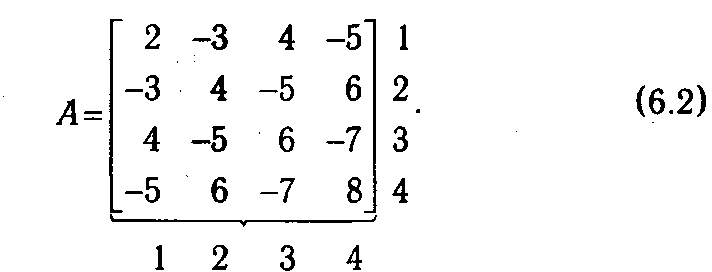
Некоторая условность и искусственность в постановке про­блемы не должны в данном случае нас смущать, так как к подоб­ной форме может быть сведена модель, описывающая, напри­мер, соревнование двух фирм за вновь открывшийся рынок сбыта продукции и т. п.

Как уже отмечалось, важнейшим в теории игр является во­прос об оптимальности решения (выбора стратегии) для каж­дого из игроков. Проанализируем с этой точки зрения некото­рую матричную игру, для которой задана платежная матрица А =║ a_ij ║ _{m x n} . При выборе игроком I стратегии i его гарантирован­ный доход независимо от действий игрока II составит min a_i,j. Поскольку он может выбирать i самостоятельно, то целесооб­разно этот выбор сделать таким, чтобы он при любой стратегии противника максимизировал величину гарантированного дохо­да, т. е. обеспечивал получение max (min a_i,j). Такой принцип вы­бора стратегии получил название «принцип максимина». С дру­гой стороны, аналогичные рассуждения могут быть проведены по поводу действий второго игрока. Его наибольший проигрыш при выборе стратегии j составит max a_i,j, и, следовательно, ему следует выбирать стратегию так, чтобы минимизировать вели­чину проигрыша при любых действиях соперника, т. е. обеспе­чить min (max a_i,j). в этом суть принципа минимакса.

Можно доказать справедливость следующего соотношения:

 

 

Однако очевидный интерес представляет ситуация, при ко­торой значение выигрыша (платежа), получаемого игроком I при выборе им максиминной стратегии, равно платежу (проиг­рышу) II-го игрока при минимаксной стратегии

 

 

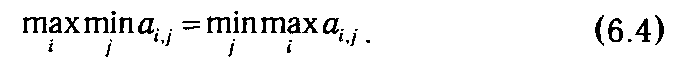
В этом случае говорят, что игра имеет седловую точку. Совпа­дение значений гарантированных выигрышей игроков при мак­симинной и минимаксной стратегии означает возможность до­стижения в игре некоторого оптимального (стабильного, равновесного) состояния, от которого невыгодно отклоняться ни одному из участников. Понятие «оптимальность» здесь озна­чает, что ни один разумный (осторожный) игрок не стремится изменить свою стратегию, так как его противник, в принципе, сможет выбрать такую стратегию, которая даст худший для первого результат. Стратегии i* и j *, образующие седловую точку, называются оптимальными, а значение v = a_i*j* называют це­ной игры. Тройка (i*, j*, v) считается решением матричной игры с седловой точкой.

Нетрудно заметить, что не всякая игра обладает седловой точкой. В частности, как игра (6.1), так и игра (6.2) седловой точки не имеют. Примером игры, имеющей седловую точку, яв­ляется игра с платежной матрицей (6.5).

 

 

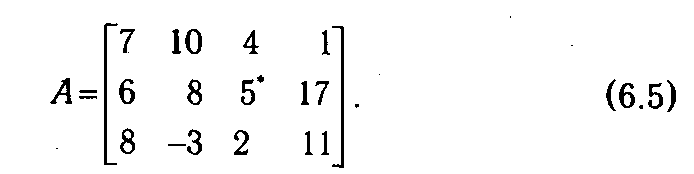
В данной матрице минимальные (гарантированные) выигрыши первого игрока по строкам равны 1, 5 и (-3). Следовательно, его максиминному выбору будет отвечать стратегия 2, гаранти­рующая выигрыш 5. Для второго игрока максимальные проиг­рыши по столбцам матрицы составят 8, 10, 5, 17, поэтому имеет смысл остановиться на стратегии 3, при которой он проиграет только 5. Таким образом, вторая стратегия первого игрока и третья стратегия второго образуют седловую точку со значени­ем 5, т. е. для игры с матрицей (6.5) имеет решение (2; 3; 5).

6.1.4. Смешанные стратегии. Дальнейшее развитие тео­рии матричных игр основывается на исследовании игры как не­которого повторяющегося процесса. Действительно, вряд ли можно дать содержательные рекомендации по такому вопросу, как следует поступать участникам однократно проводимой игры, не имеющей седловой точки. В случае же ее многократных по­второв естественной и плодотворной представляется идея ран­домизации выбора стратегий игроками, т. е. внесение в процесс выбора элемента случайности. Действительно, систематическое отклонение, например, игрока I от максиминной стратегии с це­лью увеличения выигрыша может быть зафиксировано вторым игроком и наказано. В то же время абсолютно хаотичный выбор стратегий не принесет в среднем наилучшего результата.

 

F F Смешанной стратегией игрока I в игре с матрицей A =║ a_i,j ║ _{m x n} называется упорядоченный набор действительных чисел x_i , i ∊1: m, удовлетворяющих условиям

 

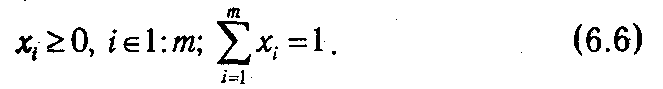
Числа интерпретируются как вероятности применения иг­роком I стратегий 1, 2,..., m, которые, в отличие от смешанных, также называют чистыми стратегиями.

Аналогично вводится понятие смешанных стратегий игрока II, которые определяются как набор чисел у_j, j ∊1: n, удовлетво­ряющих условиям

 

 

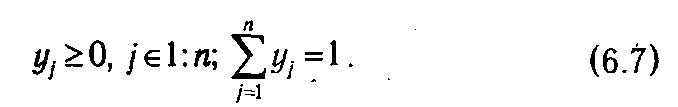
Тогда, если игрок I применяет смешанную стратегию х = (х ₁, х ₂,..., х_m) а игрок II смешанную стратегию y = (y ₁, y ₂,..., y_n), то математическое ожидание выигрыша игрока I (проигрыша игрока II) определяется соотношением

 

*

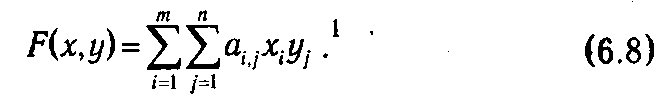* Напомним, что при многократном повторении игры средний выиг­рыш близок к математическому ожиданию.

 

В дальнейшем через Х будем обозначать множество допу­стимых смешанных стратегий игрока I, определяемое условием 6.7, а через Y — определяемое условием 6.8 множество допу­стимых смешанных стратегий игрока II.

К поиску решения игры в смешанных стратегиях, так же как и в п. 6.1.3, могут быть применены критерии максимина-минимакса. В соответствии с ними игрок I будет выбирать свою сме­шанную стратегию х = (х ₁, х ₂,..., х_m) таким образом, чтобы мак­симизировать наименьший средний выигрыш:

 

 

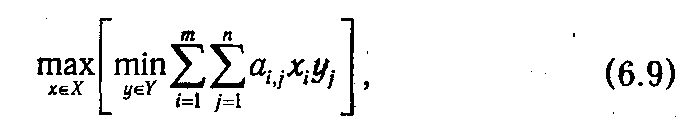
который, как можно доказать, равен

 

 

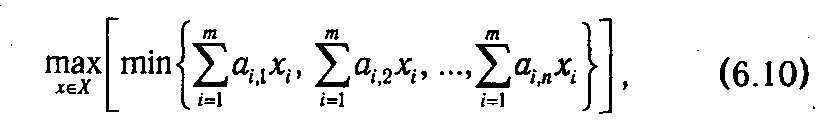
а игрок II — свою смешанную стратегию так, чтобы минимизи­ровать наибольший средний проигрыш:

 

 

также равный

 

 

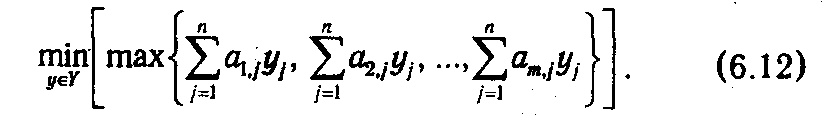
По аналогии с (6.3) для любых х ∊ Х и y ∊ Y справедливо не­равенство

 

 

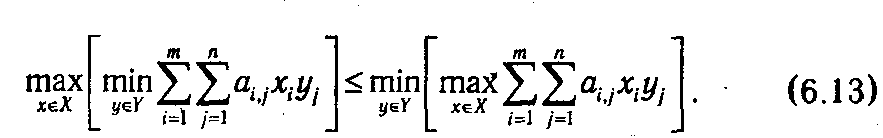
F F Стратегии х* ∊ Х и y* ∊ Y называют оптимальными смешанными стратегиями, если для любых х ∊ Х и y ∊ Y справедливо равенство

 

v =F (x*, у*) называют ценой игры, и если х* и у* существу­ют, то говорят, что игра имеет решение в смешанных стра­тегиях (х*, у*, v).

Справедлива фундаментальная теорема Дж. Неймана, кото­рую мы приведем без доказательства.

 

Теорема 6.1 (основная теорема матричных игр). Любая матричная игра имеет решение в смешанных страте­гиях.

 

Значение и нетривиальность теоремы (6.1) обусловлены прежде всего тем, что, как было показано в п. 6.1.3, в общем случае матричные игры в чистых стратегиях решения не имеют.

6.1.5. Решение матричных игр методами линейного программирования. Рассмотрим некоторые способы ре­шения матричных игр. Задача, решаемая первым игроком, (6.10) была сформулирована как максимизация наименьшей из сумм

 

 

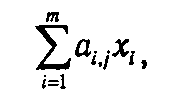
но если определить некоторое х_{m +1}, для которого выполняется

 

 

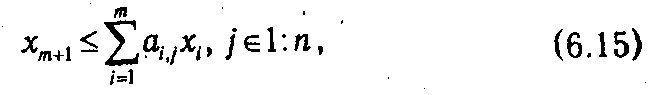
то она может быть сведена к задаче линейного программиро­вания:

 

 

при ограничениях

 

 

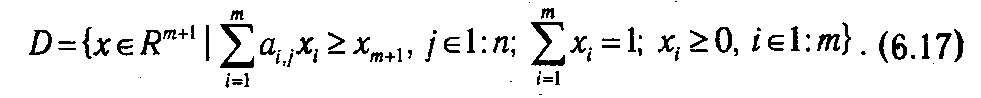
Проведя аналогичные рассуждения, приходим к тому, что задача минимизации наибольшего ожидаемого проигрыша, решаемая игроком II (6.12), сводится к задаче линейного програм­мирования

 

 

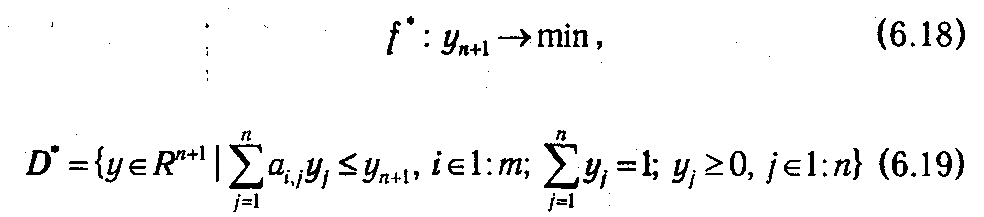
Таким образом, мы получаем возможность применять все возможности аппарата линейного программирования для поис­ка оптимальных стратегий обоих игроков.

Достаточно легко проверить, что задачи (6.16)-(6.17) и (6.18)-(6.19) образуют двойственную пару. Здесь в определен­ном смысле мы вернулись к проблемам, уже рассматривавшим­ся во второй главе, а именно к взаимосвязи между наличием ре­шения у некоторой оптимизационной задачи и существованием седловой точки у соответствующей функции Лагранжа. В дан­ном случае аналогичная связь прослеживается между седловой точкой игры и решением пары задач оптимизации.

6.1.6. Графические методы решения игр. Следует отме­тить, что применение для решения задач (6.16)-(6.17), (6.18)-(6.19) стандартных алгоритмов линейного программирования далеко не всегда является рациональным. Помимо этого суще­ствуют иные методы, которые основываются на использовании специфики данных задач. В настоящем пункте мы остановимся на очень простом классическом способе поиска оптимальных сме­шанных стратегий в матричных играх, где один из участников имеет только две стратегии (это так называемые 2 х п и т х 2 игры).

Для определенности положим, что игрок I имеет возмож­ность выбирать между двумя стратегиями с вероятностями x ₁ и x ₂ = 1- x ₁, тогда его ожидаемые выигрыши, соответствующие чистым стратегиям игрока II, примут вид

 

 

 

или

 

 

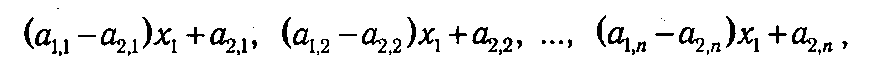
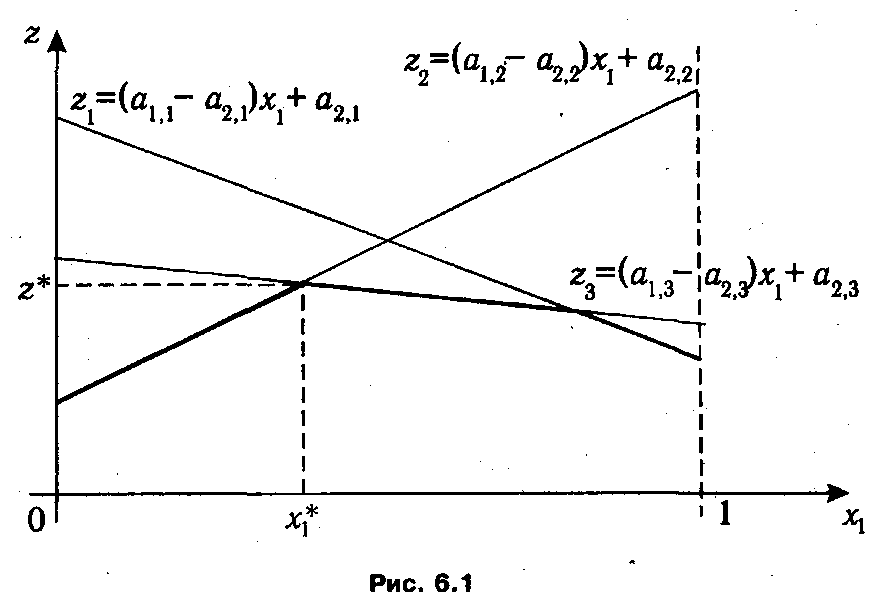
т. е. ожидаемые выигрыши могут быть представлены в виде графи­ков линейных функций, зависящих от переменной x ₁ ∊ [0; 1] (рис. 6.1, где предполагается, что игрок II имеет три стратегии).

Линии, изображенные на рис. 6.1, задают зависимости сред­него выигрыша игрока I от значения вероятности x ₁ , с которой он выбирает свою первую стратегию, для случаев, когда его противник выбирает первую, вторую или третью чистую стра­тегию. Тогда значениям минимального гарантированного дохо­да первого игрока соответствует нижняя огибающая всех трех прямых. Согласно принципу максимина, оптимальному выбору игрока I будет соответствовать наивысшая точка, лежащая на данной огибающей, отмеченная на рисунке как (x ₁*, z*). Зная ее, можно определить оптимальную смешанную стратегию перво­го игрока х * = (x ₁*, 1- x ₂*) и цену игры, равную z*.

Исходя из отношения двойственности, которым, как было ус­тановлено в п. 6.1.5, связаны задачи обоих игроков, по оптималь­ной стратегии первого участника х * однозначно определяется оптимальная стратегия его противника у*. Поскольку у* явля­ется результатом решения задачи линейного программирова­ния, то он обладает всеми свойствами допустимого базисного плана, т. е. в случае 2 х п игры имеет не более чем две ненулевых компоненты и не менее чем (п -2) нулевых. Номера ненулевых элементов у* определяются номерами линий, пересечение кото­рых определило оптимальную стратегию первого игрока. Дей­ствительно, игрок II знает оптимальную стратегию соперника, и применение им стратегий, соответствующих прямым, проходя­щим выше точки (х ₁*, z *), только увеличило бы его проигрыш.

В рассматриваемом примере это линии z ₂ и z ₃, и, следова­тельно, в своей оптимальной стратегии второй игрок должен с ненулевыми вероятностями применять вторую и третью чистые стратегии (у ₂>0, у ₃ >0). На основе этого, а также учитывая условие нормировки

 

 

можем выразить: y ₃ = l – y ₂ тогда оптимальное значение y ₂* мо­жет быть найдено из условия

 

 

или

 

В результате получаем оптимальную стратегию игрока II у*= (0, у ₂*, у ₃*).

Очевидно, что поиск решения в игре т х 2 осуществляется аналогичным образом с точностью до наоборот: строятся гра­фики ожидаемого проигрыша игрока II, находится их верхняя огибающая и т. д.

Безусловно, графический способ в силу ограниченности круга задач, к которым он может быть применен, имеет скорее теоретическое, чем практическое значение. Однако он хорошо иллюстрирует содержательную сторону процесса поиска реше­ния в игре.