Вычислить интегралы:
1. Непосредственное интегрирование

Ответы: 
2. Метод подстановки

Ответы: 
Лекция 3. Геометрическое приложение определенного интеграла. Вычисление площадей
3.1. Вычисление площадей
1) Если фигура ограничена линиями: y = f(x), OX, x = a, x = b (т.е. площадь криволинейной трапеции)

2) Если фигура ограничена графиками двух функций: 

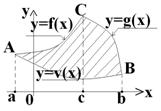 3) Если фигура ограничена графиками нескольких непрерывных функций – свести задачу к задаче 2).
3) Если фигура ограничена графиками нескольких непрерывных функций – свести задачу к задаче 2).
Например: на рисунке фигура ограничена графиками функций 
Точкой С разбиваем отрезок [a, b] на два. Тогда:
 или
или 
3.2. Практическая работа № 10 «Вычисление площадей плоских фигур»
Найти площадь фигуры, ограниченной линиями:
1)  сделаем схематичный рисунок. График функции выше оси абсцисс, значит – это криволинейная трапеция.
сделаем схематичный рисунок. График функции выше оси абсцисс, значит – это криволинейная трапеция.

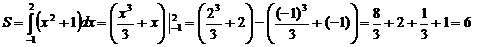
Ответ: 6 ед2
 2)
2) 
График функции ниже оси абсцисс, значит площадь:
 Ответ: 6 ед2
Ответ: 6 ед2
 3)
3)  . См. рисунок: на заданном отрезке фигуру разбиваем на две части:
. См. рисунок: на заданном отрезке фигуру разбиваем на две части:
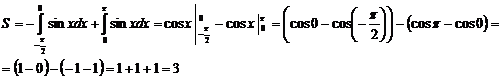 Ответ: 3 ед2
Ответ: 3 ед2
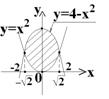
4)  (a?, b?)
(a?, b?)
1) Ищем пределы интегрирования: это точки, в которых графики пересекаются. Составляем уравнение:  ;
;
2) Фигура ограничена графиками четных функций, значит, она симметрична относительно оси Y. Тогда удобнее найти половину площади и умножить на 2.  Ответ:
Ответ: 
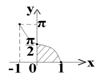 5)
5)  чтобы найти площадь данной фигуры, придется применить интегрирование по частям.
чтобы найти площадь данной фигуры, придется применить интегрирование по частям.

Ответ: 
 2018-01-08
2018-01-08 647
647








