Лекция 1. Определение, геометрический смысл и свойства определенного интеграла

1.1. Определенный интеграл как предел интегральных сумм

Пусть дана функция y = f(x) на отрезке [a, b], причем f ^/(x) ≥ 0 для любого .

Задача. Найти площадь фигуры ABCD (криволинейная трапеция)

Фигура разбивается на n прямоугольников, ширина которых , высота – .

Тогда приближенно площадь каждого прямоугольника:

Просуммировав площади всех прямоугольников, получим приближенное значение площади искомой фигуры:

(1) (интегральная сумма)

Величина Δ x – шаг разбиения. При уменьшении шага разбиения Δ x → 0, т.е. количество разбиений n → ∞. При этом формула (1) станет более точной. Тогда точное значение площади – предел (если он существует).

Определение. Если последовательность интегральных сумм S _n при n → ∞ имеет конечный предел, не зависящий от способа разбиения отрезка [a, b] и от выбора точки ξ _I, то этот предел называют определенным интегралом функции f(x) в промежутке от a до b.

(2) 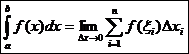т.е. интеграл – это сумма

Значения a и b – соответственно нижний и верхний пределы интегрирования. Таким образом, определенный интеграл представляет собой число, а не формулу в отличие от неопределенного интеграла.

В виде формулы (2) определение впервые сформулировано немецким математиком Бернардом Риманом. Поэтому интегральную сумму часто называют римановской суммой, а интеграл – интегралом Римана. Знак ∫ введен Лейбницем, это удлиненная первая буква от латинского слова «summa».

1.2. Геометрический смысл определенного интеграла

Если интегрируемая функция , то определенный интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции y = f(x), осью абсцисс и прямыми x=a и x=b,

В этом заключается геометрический смысл определенного интеграла. При этом:

1.3. Свойства определенного интеграла

1) Постоянный множитель можно выносить за знак интеграла: ;

2) О.И. от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов: ;

3) Если , то:

4) Если f(x) ≥ 0 на [a, b], то ; 5) ;

6) Если f(x) ≥ g(x) для любого x из [a, b], то

Площадь фигуры, заключенной между графиками:

(Из функции, график которой лежит выше, вычитается функция, график которой лежит ниже);

 

7) Теорема о среднем. Если функция f(x) непрерывна на [a, b], то существует такая точка с из [a, b], что: Т.е. площадь криволинейной трапеции может быть найдена как площадь прямоугольника.