Найти площадь фигуры, ограниченной линиями: Часть 1.
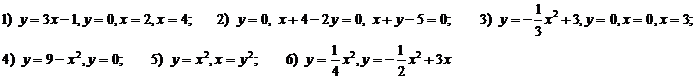 Ответы:
Ответы:  (ед2)
(ед2)
Часть 2.
1)  ; 2)
; 2)  ; 3)
; 3) 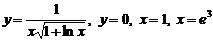 ; 4)
; 4)  ; 5)
; 5) 
Ответы:  (ед2)
(ед2)
Лекция 4. Геометрическое приложение определенного интеграла. Вычисление объемов
4.1. Вычисление объемов тел вращения
Тело вращения – это тело, полученное вращением плоской фигуры вокруг одной из сторон. В нашем случае вращаемая фигура – это криволинейная трапеция. Вращать ее можно вокруг оси X и вокруг оси Y (тела при этом получаются разные).
Пусть функция f(x) непрерывна на отрезке [a, b]. Тогда объем тела, полученного вращением рассматриваемой криволинейной трапеции:
1. Вокруг оси X:
 Заштрихованная в диагональ фигура – это исходная криволинейная трапеция.
Заштрихованная в диагональ фигура – это исходная криволинейная трапеция.
Заштрихованный эллипс – это круг радиуса R, который получается при вращении выделенного отрезка вокруг оси X. Площадь этого круга:

Тогда объем: 
2. Вокруг оси Y: 
Т.е. здесь нужно выразить x через y и вычислить пределы интегрирования.
4.2. Решение задач
 1) Получим знакомую формулу для вычисления объема конуса
1) Получим знакомую формулу для вычисления объема конуса 
Конус получается вращением прямоугольного Δ LOh вокруг OX.
Сверху фигура ограничена прямой; это график линейной функции 
Тогда: 
При условии, что  , имеем
, имеем 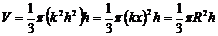
2) Вычислить объем тела, полученного при вращении фигуры, ограниченной линиями:  вокруг OX.
вокруг OX.
 Это тело называется параболоид вращения
Это тело называется параболоид вращения
 – это верхняя часть параболы
– это верхняя часть параболы 
 Ответ: 32π ед3
Ответ: 32π ед3
3) Вычислить объем тела, полученного при вращении фигуры, заключенной между графиками функций

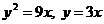 вокруг OY.
вокруг OY.
1. Сначала строим тело, о котором идет речь. Оно получено вращением заштрихованной фигуры вокруг оси Y.
2. Определяем пределы интегрирования: c = o, d =?
Значение d соответствует точке, в которой пересекаются графики.
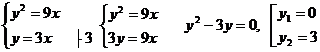 т.е. d = 3
т.е. d = 3
3. Подынтегральная функция:

4. По формуле: 
Ответ: 0,4 π ед3
 2018-01-08
2018-01-08 961
961








