3.1. Случайные величины и законы распределения
Переменная величина называется случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями. Наиболее полной, исчерпывающей характеристикой случайной величины является закон распределения.
Закон распределения – функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина Х принимает определенное значение хi или попадает в некоторый интервал.
Функция распределения случайной величины X - вероятность того, что случайная величина Х (дискретная или непрерывная) принимает значение, меньшее х. Обозначается F (x): 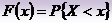 .
.
Функция распределения является универсальным видом закона распределения, пригодным для любой случайной величины.
· Случайная величина Х называется дискретной, если существует такая неотрицательная функция 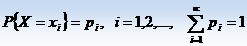 , которая ставит в соответствие значению хi переменной Х вероятность рi, с которой она принимает это значение. Дискретную величину удобно задавать таблицей значений
, которая ставит в соответствие значению хi переменной Х вероятность рi, с которой она принимает это значение. Дискретную величину удобно задавать таблицей значений
· Случайная величина Х называется непрерывной, если для любых a < b существует такая неотрицательная функция f (x), что 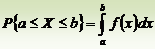 .
.
Функция f (x) называется плотностью распределения непрерывной случайной величины,
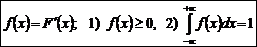 . Для непрерывной случайной величины функция F(x) – интегральная функция распределения.
. Для непрерывной случайной величины функция F(x) – интегральная функция распределения.

Общие свойства функции распределения:
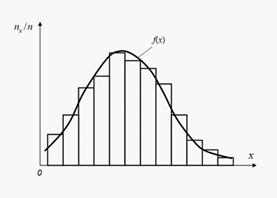
Каждый закон распределения – это некоторая функция, полностью описывающая случайную величину с вероятностной точки зрения. На практике о распределении вероятностей случайной величины Х часто приходится судить только по результатам испытаний. При большом числе испытаний n отношение 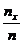 (частоты попадания в интервалы) должны быть близки к вероятностям попадания в эти интервалы. Зависимость частот
(частоты попадания в интервалы) должны быть близки к вероятностям попадания в эти интервалы. Зависимость частот 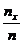 от интервалов определяет эмпирическое распределение вероятностей случайной величины Х, графическое представление которой называется гистограммой.
от интервалов определяет эмпирическое распределение вероятностей случайной величины Х, графическое представление которой называется гистограммой.
На рисунке изображена гистограмма и выравнивающая
Однако, часто бывает достаточно указать только отдельные числовые параметры, характеризующие основные свойства распределения. Эти числа называются числовыми характеристиками случайной величины.
3.2. Числовые характеристики случайной величины
1. Математическое ожидание случайной величины - аналог среднего арифметического.
- Для дискретной –
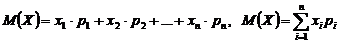
- Для непрерывной - интеграл от произведения ее значений х на плотность распределения вероятностей f (x):
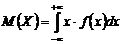 .
.
2. Дисперсия – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
- Для дискретной случайной величины –
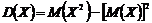 ;
; - Для непрерывной случайной величины –
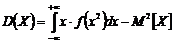 ;
;
3. Среднее квадратичное отклонение - показывает разброс значений случайной величины вокруг ее математического ожидания.
Для дискретной и непрерывной величины – 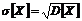
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Однако, это уже программа для высших учебных заведений.
3.3. Практическая работа № 12 «Нахождение числовых характеристик случайной величины»
Пример 1. Интегральная функция распределения непрерывной случайной величины, определенной на интервале 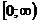 , имеет вид
, имеет вид 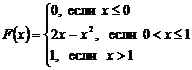 .
.
1) Найти плотность распределения, математическое ожидание, дисперсию и квадратичное отклонение случайной величины; 2) Построить графики функций F(x), f(x).
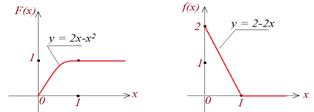 Решение.
Решение. 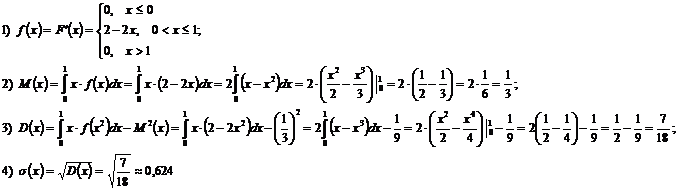
Пример 2. Дан следующий вариационный ряд:
| i | ||||||||||
| xi |
Задание: 1) построить полигон частот;
2) вычислить математическое ожидание, дисперсию, среднее квадратичное отклонение, моду, медиану;
3) построить функцию распределения.
Решение. 1) Дана выборка объема n = 10. Составим таблицу распределения частот:
| xi | ||||
| ni |
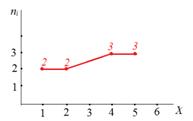
Тогда, график полигона частот:
2) 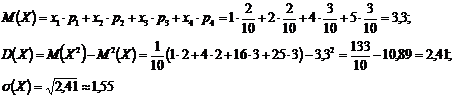
Мода равна варианту, имеющему наибольшую частоту: 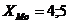 - две моды;
- две моды;
Медиана равна среднему варианту выборки: 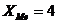 ;
;
3) Чтобы найти функцию распределения, составим таблицу вероятностей:
| xi | ||||
| pi | 0,2 | 0,2 | 0,3 | 0,3 |
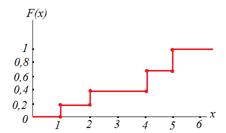
Тогда функция распределения: 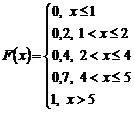
 2018-01-08
2018-01-08 5421
5421
