Контрольная работа № 1
К задаче № 1
В качестве примера решения задачи № 1 проведем исследование кривошипно-ползунного механизма (см. рис. 1). Примем следующие исходные данные: входное (ведущее) звено 1 (кривошип АВ) вращается по часовой стрелке с угловой скоростью 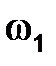 = 12 рад / с (по условию
= 12 рад / с (по условию 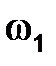 = const); угол мгновенного положения
= const); угол мгновенного положения 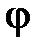 = 70 °; размеры звеньев:
= 70 °; размеры звеньев: 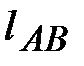 = 0,08 м,
= 0,08 м, 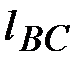 = 0,18 м,
= 0,18 м, 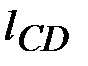 = 0, 22 м; центры тяжести
= 0, 22 м; центры тяжести 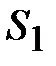 и
и 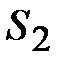 звеньев расположены посередине каждого звена (на чертеже - точки
звеньев расположены посередине каждого звена (на чертеже - точки 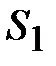 и
и 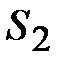 ); центр тяжести
); центр тяжести 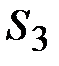 третьего звена (ползуна) совпадает с точкой С.
третьего звена (ползуна) совпадает с точкой С.
1. Структурный анализ механизма
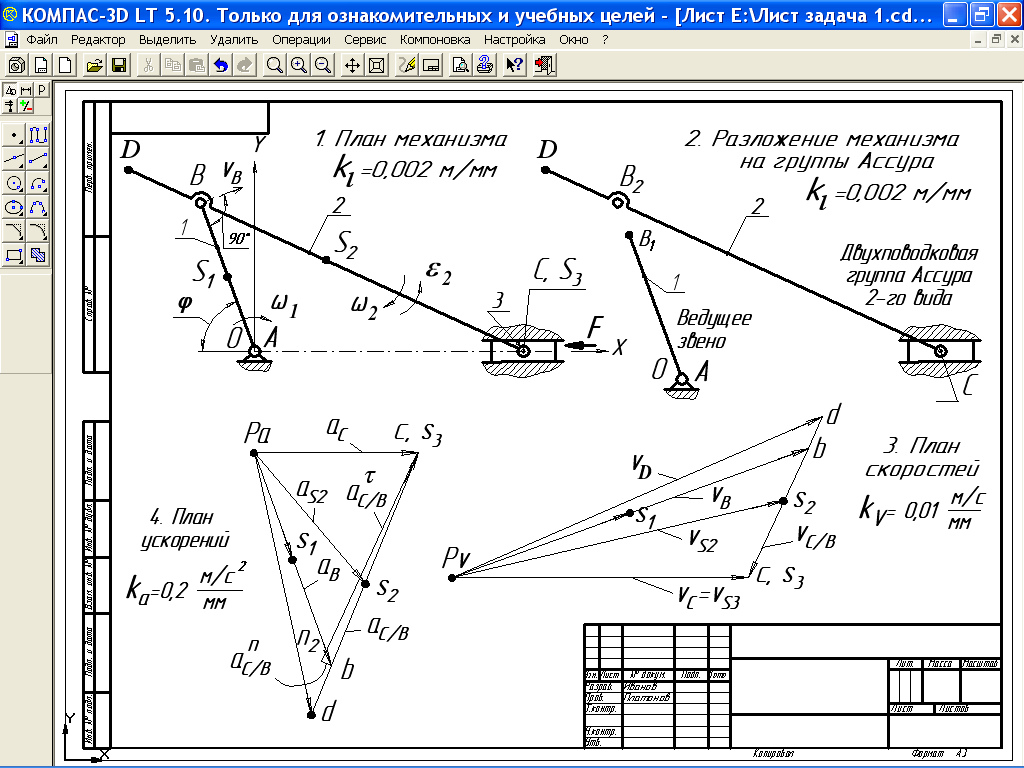
По исходным данным вычерчиваем схему механизма в произвольно выбранном (но удобном для построения) масштабе. Графическая часть структурного и кинематического анализа выполняется на одном листе формата А4 или А3 (см. рис. 9). С учетом того, что действительная длина входного звена 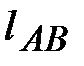 = 0,08 м, примем длину отрезка, изображающего действительную величину звена АВ на чертеже равной, например, 40 мм. Тогда расчетный масштаб построения схемы механизма определится как:
= 0,08 м, примем длину отрезка, изображающего действительную величину звена АВ на чертеже равной, например, 40 мм. Тогда расчетный масштаб построения схемы механизма определится как:
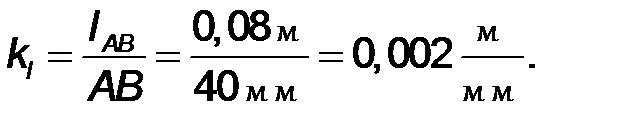
Размеры (в мм) остальных звеньев для их вычерчивания на схеме механизма определяются соответственно:
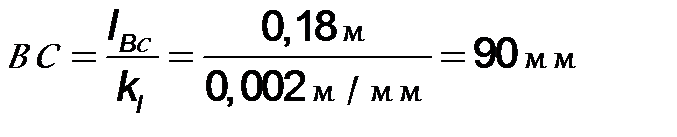 ;
; 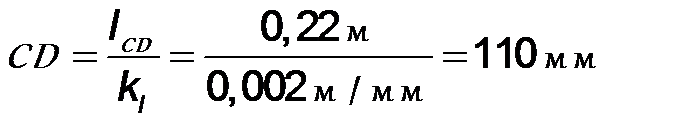 .
.
Построение схемы механизма в масштабе (т.е. плана механизма) начинаем с выбора точки О - начала отсчета системы координат Х-У (см. рис. 9).
Степень подвижности 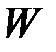 механизма определяется по формуле Чебышева:
механизма определяется по формуле Чебышева:
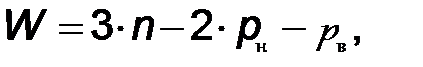
где 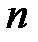 - число подвижных звеньев механизма;
- число подвижных звеньев механизма; 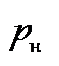 - число низших кинематических пар;
- число низших кинематических пар; 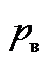 - число высших кинематических пар.
- число высших кинематических пар.
Для данной схемы число подвижных звеньев механизма 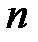 = 3 (кривошип АВ, шатун ВС, а также ползун, обозначенный как звено 3), число подвижных соединений звеньев низшего класса
= 3 (кривошип АВ, шатун ВС, а также ползун, обозначенный как звено 3), число подвижных соединений звеньев низшего класса 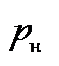 = 4, число подвижных соединений звеньев высшего класса
= 4, число подвижных соединений звеньев высшего класса 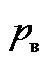 = 0. Следовательно,
= 0. Следовательно,
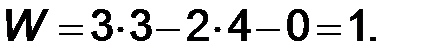
Это означает, что для работы рассматриваемого механизма достаточно задать закон движения только одному звену (в данном случае - звену 1, которое является входным, т.е. ведущим). При этом законы движения остальных звеньев механизма будут вполне определенными и однозначными.
Разложение механизма на группы Ассура начинается с наиболее простой и наиболее удаленной от ведущего звена группы. При разложении механизма обязательно следует соблюдать взаимное расположение звеньев. Простейшая группа Ассура представляет собой сочетание двух звеньев и трех кинематических пар. Для заданного механизма такую группу составляют звенья 2 и 3, а также три кинематические пары: две вращательные (В, которую образуют звенья 1 и 2, и С, которую образуют звенья 2 и 3) и одна поступательная С (звенья 3 и 0). Эта группа является группой Ассура 2 класса 2 порядка.
Оставшаяся часть механизма (ведущее звено АВ и вращательная кинематическая пара А (0-1)) имеет степень подвижности 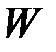 = 1 и относится к механизмам 1 класса. Таким образом, исследуемый механизм является механизмом 2 класса 2 порядка.
= 1 и относится к механизмам 1 класса. Таким образом, исследуемый механизм является механизмом 2 класса 2 порядка.
2. Кинематический анализ механизма
Кинематическое исследование механизма ведется для каждой структурной группы в порядке их присоединения. Порядок расчета приведен в табл.11.

 Кинематический анализ механизма
Кинематический анализ механизма
| № п/п | Определяемая величина | Расчетная формула | Результат расчета | Методические указания | |
| 1. Определение линейных и угловых скоростей | |||||
| 1.1 | Скорость
точки В
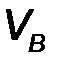
|
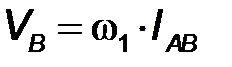 =
= =
= 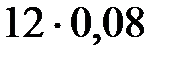 = =
| 0,96 м/с | Рассмотрим группу Ассура 2-3 и определим
линейные скорости точек этой группы. Первой такой точкой является точка В, которая относительно
точки А совершает вращательное движение.
Вектор скорости точки В направлен в сторону
вращения 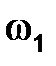 перпендикулярно звену АВ
(см. рис. 9, план скоростей) перпендикулярно звену АВ
(см. рис. 9, план скоростей)
| |
| 1.2 | Масштаб плана скоростей
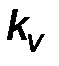
| 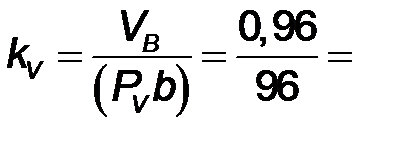
| 0,01 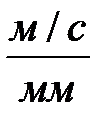
| Из произвольно выбранной точки 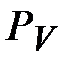 (полюс плана скоростей: начало отсчета) отложить перпендикулярно звену АВ отрезок ( (полюс плана скоростей: начало отсчета) отложить перпендикулярно звену АВ отрезок (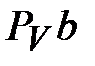 ) (например, ( ) (например, (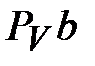 ) = 96 мм: выбирается произвольно), который на схеме изображает величину вектора скорости т. В ( ) = 96 мм: выбирается произвольно), который на схеме изображает величину вектора скорости т. В (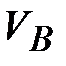 =0,96 м/с) =0,96 м/с)
| |
| 1.3 | Скорость
точки С
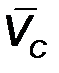
|
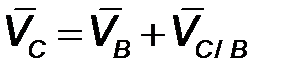
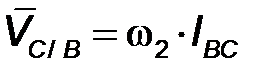 =?
(направлен ^ ВС) =?
(направлен ^ ВС)
| Следующая точка - точка С. На основании теоремы о сложении скоростей в сложном движении точки С ее скорость движения точки С вокруг точки В). Величина скорости |


| № п/п | Определяемая величина | Расчетная формула | Результат расчета | Методические указания |
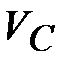 // оси ОХ // оси ОХ
| перпендикулярно радиусу относительного вращения (т.е. звену ВС).
Точка С движется возвратно-поступательно вдоль оси ОХ, поэтому полный вектор 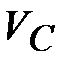 скорости
точки С направлен параллельно оси ОХ скорости
точки С направлен параллельно оси ОХ
| |||
Из плана
скоростей:
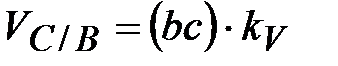 =
= 36·0,01 = =
= 36·0,01 =
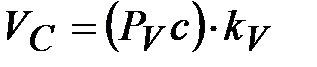 =
= 75·0,01 = =
= 75·0,01 =
| = 0,36 м/с = 0,75 м/с | Из точки «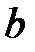 » плана скоростей провести прямую перпендикулярно звену ВС, а из полюса » плана скоростей провести прямую перпендикулярно звену ВС, а из полюса 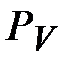 -
прямую, параллельно оси ОХ (т.е. параллельно
направляющей). Их пересечение определяет
положение точки « -
прямую, параллельно оси ОХ (т.е. параллельно
направляющей). Их пересечение определяет
положение точки «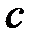 ». Направление векторов
скоростей осуществляется в соответствии
с векторным уравнением для точки С.
Значение скоростей ». Направление векторов
скоростей осуществляется в соответствии
с векторным уравнением для точки С.
Значение скоростей 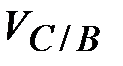 и и 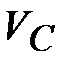 (в м/с) определяют из плана скоростей измерением отрезков (в м/с) определяют из плана скоростей измерением отрезков 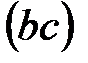 и и 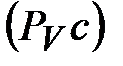 , и умножением этих значений на величину масштаба скорости , и умножением этих значений на величину масштаба скорости 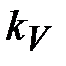
| ||
| 1.4 | Угловая
скорость звена 2 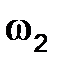
| 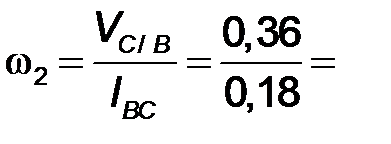
| 2 рад/с | Для определения направления угловой скорости 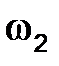 необходимо условно перенести в точку С механизма вектор скорости необходимо условно перенести в точку С механизма вектор скорости 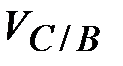 , а точку В условно закрепить. Тогда вектор , а точку В условно закрепить. Тогда вектор 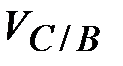 будет вращать точку С
относительно В по часовой стрелке. будет вращать точку С
относительно В по часовой стрелке.
|

 №
п/п №
п/п
| Определяемая величина | Расчетная формула | Результат расчета | Методические указания |
| 1.5 | Скорость
точки D
механизма 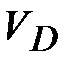 . .
| 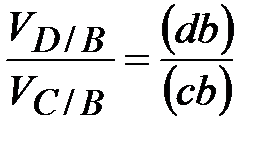 Отсюда:
Отсюда:
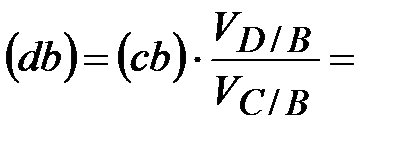
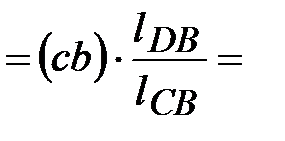 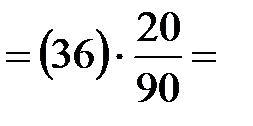
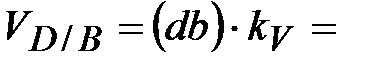 =
= 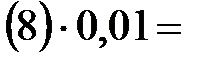
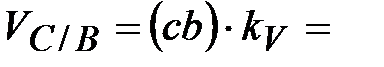 =
= 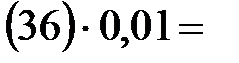
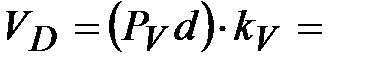
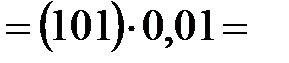
| 8 мм 0,08 м/с 0,36 м/с 1,01 м/с |
Положение точек «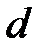 », « », «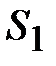 », « », «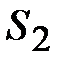 » и « » и «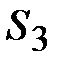 »
на плане скоростей определяется на основании
свойства подобия
(скорости точек D и С при их вращении
вокруг точки В соотносятся также,
как и аналогичные отрезки)
Скорость точки D при ее вращении вокруг точки В
Скорость точки С при ее вращении вокруг точки В
От точки « »
на плане скоростей определяется на основании
свойства подобия
(скорости точек D и С при их вращении
вокруг точки В соотносятся также,
как и аналогичные отрезки)
Скорость точки D при ее вращении вокруг точки В
Скорость точки С при ее вращении вокруг точки В
От точки «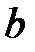 » на прямой » на прямой 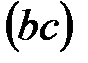 отложить отрезок отложить отрезок 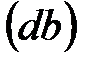 =8 мм и соединить полученную точку « =8 мм и соединить полученную точку «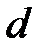 »
с полюсом »
с полюсом 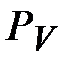 . Вектор . Вектор 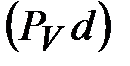 графически
изображает скорость точки D механизма. графически
изображает скорость точки D механизма.
|

| № п/п | Определяемая величина | Расчетная формула | Результат расчета | Методические указания |
| 1.6 | Скорости
точек центров
тяжести
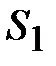 , , 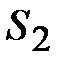 и и 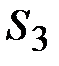 звеньев
( звеньев
(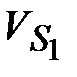 , , 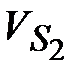 и и 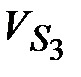 ). ).
|
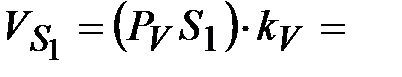
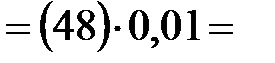
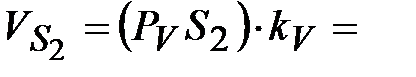
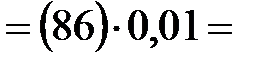
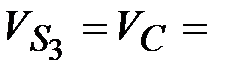
| 0,48 м/с 0,86 м/с 0,75 м/с | Точки центров тяжести 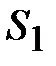 и и 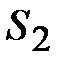 звеньев
расположены посередине длин соответствующих звеньев, а центр тяжести звеньев
расположены посередине длин соответствующих звеньев, а центр тяжести 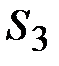 расположен в шарнире С (см. задание). Поэтому точки « расположен в шарнире С (см. задание). Поэтому точки «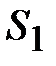 » и « » и «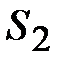 » будут расположены на плане скоростей посередине
отрезков » будут расположены на плане скоростей посередине
отрезков 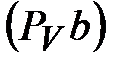 и и 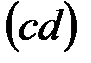 , а скорость точки , а скорость точки 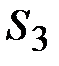 будет равна скорости точки С. Значения скоростей точек будет равна скорости точки С. Значения скоростей точек
 (в м/с) определяют из плана скоростей измерением соответствующих отрезков и умножением этих
значений на величину масштаба скорости (в м/с) определяют из плана скоростей измерением соответствующих отрезков и умножением этих
значений на величину масштаба скорости 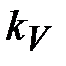
|
| 2. Определение линейных и угловых ускорений | ||||
| 2.1 | Ускорение точки В
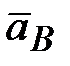
|
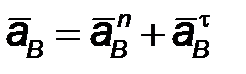
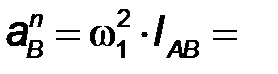
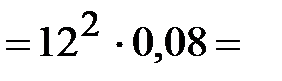 (направлено вдоль звена АВ от точки В
к точке А)
(направлено вдоль звена АВ от точки В
к точке А)
|
11,5 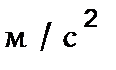
| Рассмотрим группу Ассура 2-3
и определим линейные ускорения точек
этой группы. Первой точкой является точка В.
В общем виде ускорение любой точки можно
представить как векторную сумму
нормального 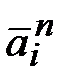 и тангенциального и тангенциального 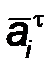 ускорений
Абсолютная величина нормального ускорения равна ускорений
Абсолютная величина нормального ускорения равна 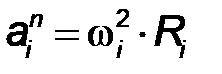 , где , где 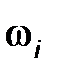 - угловая скорость звена (рад/с), - угловая скорость звена (рад/с), 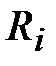 - радиус вращения звена, м.
Вектор нормального ускорения направлен вдоль
радиуса от точки к центру ее вращения. - радиус вращения звена, м.
Вектор нормального ускорения направлен вдоль
радиуса от точки к центру ее вращения.
|

 №
п/п №
п/п
| Определяемая величина | Расчетная формула | Результат расчета | Методические указания |
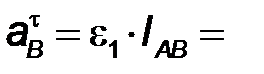
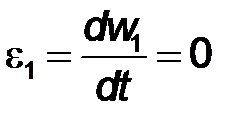 (т.к.
(т.к. 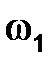 = const) = const)
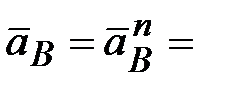
|
0 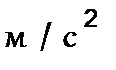 11,5
11,5 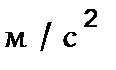
| Абсолютная величина тангенциального ускорения равна 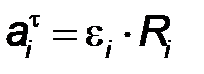 , где , где 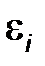 - угловое ускорение звена.
Вектор тангенциального ускорения направлен
перпендикулярно нормальному ускорению
(т.е. звену) в сторону углового ускорения.
Т.к. угловая скорость - угловое ускорение звена.
Вектор тангенциального ускорения направлен
перпендикулярно нормальному ускорению
(т.е. звену) в сторону углового ускорения.
Т.к. угловая скорость 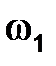 = const, то = const, то 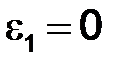 и и 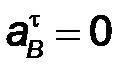 . Следовательно, ускорение . Следовательно, ускорение 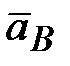 для точки В
определится величиной нормального ускорения для точки В
определится величиной нормального ускорения 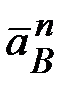 . .
| ||
| 2.2 | Масштаб плана ускорений
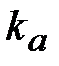
| 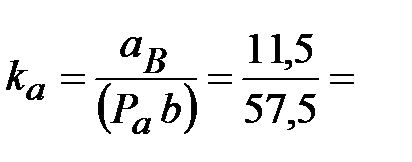
| 0,2 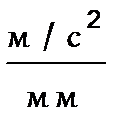
| Из произвольной точки 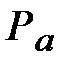 (полюс плана ускорений - начало отсчета) отложить параллельно звену АВ отрезок (полюс плана ускорений - начало отсчета) отложить параллельно звену АВ отрезок 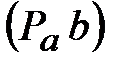 = 57,5 мм, который в масштабе = 57,5 мм, который в масштабе 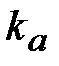 изображает величину вектора ускорений точки В
(рис. 9, план ускорений) изображает величину вектора ускорений точки В
(рис. 9, план ускорений)
|
| 2.3 | Ускорение точки С
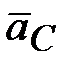
|
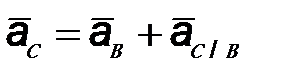
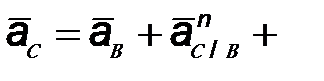
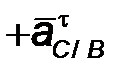
| Общее ускорение точки С складывается
из ускорения точки В и ускорения точки С
при ее вращении вокруг точки В.
Ускорение точки С при ее вращении вокруг точки В (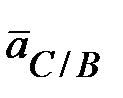 ) может быть разложено на нормальное ) может быть разложено на нормальное 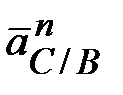 и тангенциальное и тангенциальное 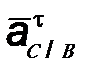 ускорения, которые
определяются согласно выражениям,
приведенным в пункте 2.1 данной таблицы ускорения, которые
определяются согласно выражениям,
приведенным в пункте 2.1 данной таблицы
|

 Продолжение табл. 11
Продолжение табл. 11
| № п/п | Определяемая величина | Расчетная формула | Результат расчета | Методические указания |
Нормальное
ускорение
точки С при
ее вращении
вокруг точки В
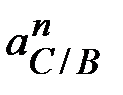 Тангенциальное
ускорение
точки С при
ее вращении
вокруг точки В
Тангенциальное
ускорение
точки С при
ее вращении
вокруг точки В
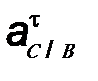
|
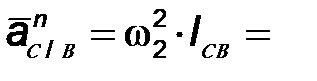
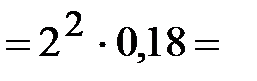 (направлено // ВС от точки С к точке В)
(направлено // ВС от точки С к точке В)
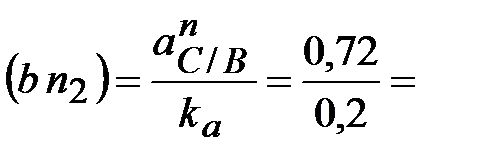
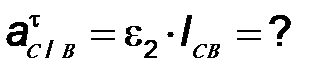
|
0,72 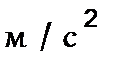 3,6 мм
3,6 мм
| Полученные уравнения решаем
графоаналитическим методом.
Отрезок 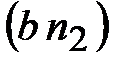 = 3,6 мм, представляющий
в масштабе = 3,6 мм, представляющий
в масштабе 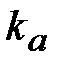 вектор ускорения вектор ускорения 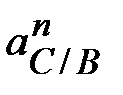 , отложить
от точки « , отложить
от точки «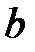 » плана ускорений в направлении от
точки С к точке В механизма (рис. 9, план ускорений).
Величина ускорения » плана ускорений в направлении от
точки С к точке В механизма (рис. 9, план ускорений).
Величина ускорения 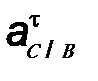 остается неизвестной,
т.к. остается неизвестной,
т.к. 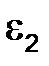 =? Известно лишь, что =? Известно лишь, что 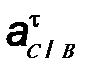 ^ ВС.
Поскольку нормальное и тангенциальное ускорения
взаимно перпендикулярны, то через точку ^ ВС.
Поскольку нормальное и тангенциальное ускорения
взаимно перпендикулярны, то через точку 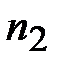 плана ускорений проводим прямую,
перпендикулярную отрезку
плана ускорений проводим прямую,
перпендикулярную отрезку 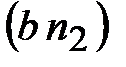 до пересечения
с горизонтальной прямой - линией действия
ускорения точки С, проведенной
из полюса Р. Точку пересечения обозначаем « до пересечения
с горизонтальной прямой - линией действия
ускорения точки С, проведенной
из полюса Р. Точку пересечения обозначаем «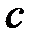 ». ».
|

 №
п/п №
п/п
| Определяемая величина | Расчетная формула | Результат расчета | Методические указания | |
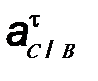
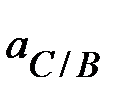
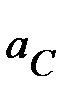
|
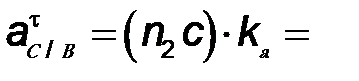
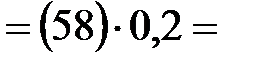 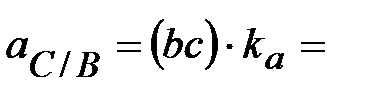
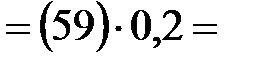
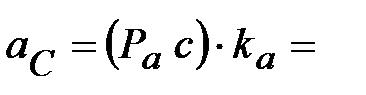
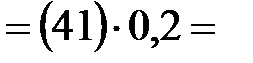
|
11,6 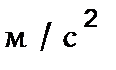 11,8
11,8 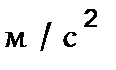 8,2
8,2 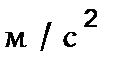
|
Значения ускорений (м/с 2 ) определяют из
плана ускорений измерением соответствующих
отрезков и умножением этих значений на
величину масштаба плана ускорений 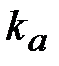 . .
| ||
| 2.4 | Угловое
ускорение
звена 2
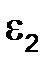
| 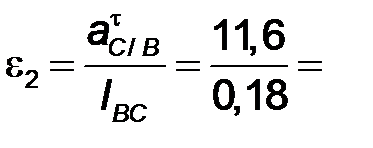
| 64,4 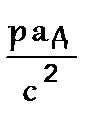
| Для определения направления вектора углового
ускорения 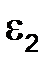 необходимо условно перенести вектор тангенциального ускорения необходимо условно перенести вектор тангенциального ускорения 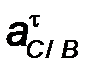 в точку С
механизма, а точку В - условно закрепить. Тогда
искомый вектор будет вращать точку С
относительно точки В против часовой стрелки. в точку С
механизма, а точку В - условно закрепить. Тогда
искомый вектор будет вращать точку С
относительно точки В против часовой стрелки.
| |
| 2.5 | Ускорения центров
тяжести
звеньев (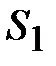 , , 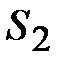 и и 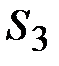 ) и точки D ) и точки D
| 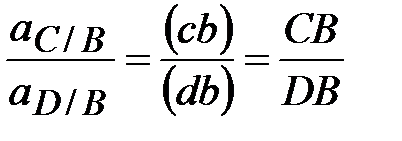 Отсюда: Отсюда:
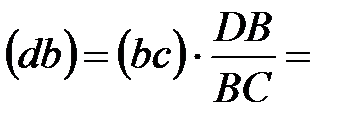 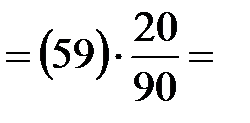
| 13,1 мм | Положение центров тяжести звеньев
определяется на основании свойств планов скоростей и ускорений (см. пункт 1.5 данной таблицы). От точки «
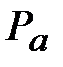 . .
|


| № п/п | Определяемая величина | Расчетная формула | Результат расчета | Методические указания |
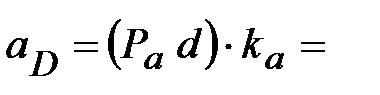
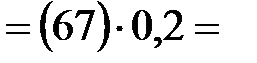
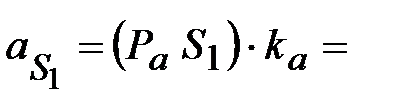
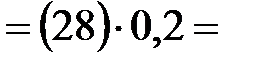
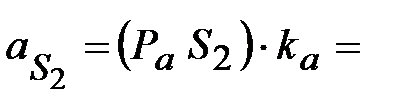
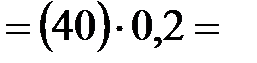
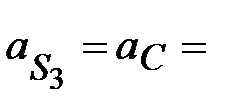
|
13,4 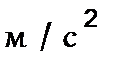 5,6
5,6 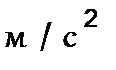 8
8 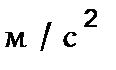 8,2
8,2 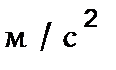
| План ускорений построен
в масштабе 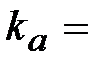 0,2 0,2 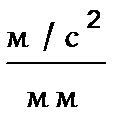 Значения ускорений точек
Значения ускорений точек 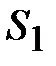 , , 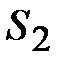 , , 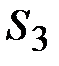 и D
(в м/с 2 ) определяют из плана ускорений
измерением соответствующих
отрезков и умножением этих значений на
величину масштаба ускорений и D
(в м/с 2 ) определяют из плана ускорений
измерением соответствующих
отрезков и умножением этих значений на
величину масштаба ускорений 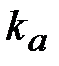 .
Вектор .
Вектор 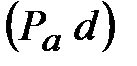 изображает в масштабе ускорение точки D механизма ( изображает в масштабе ускорение точки D механизма (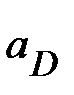 )
Вектор )
Вектор 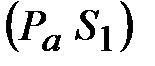 изображает в масштабе ускорение точки изображает в масштабе ускорение точки 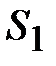 механизма ( механизма (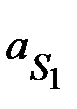 )
Вектор )
Вектор 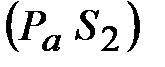 изображает в масштабе ускорение точки изображает в масштабе ускорение точки 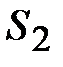 механизма ( механизма (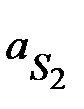 )
Ускорение точки )
Ускорение точки 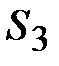 равно ускорению точки С, т.к. центр тяжести равно ускорению точки С, т.к. центр тяжести 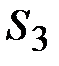 расположен в шарнире С расположен в шарнире С
|

| (Шифр студента) |
| РГОТУПС |
| Структурный и кинематический анализ механизма |
| Рис. 9. Структурный и кинематический анализ механизма |

Задача № 2
К стальному круглому валу (рис. 15, а) приложены вращающие вал моменты 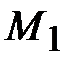 = 2,5 кН·м,
= 2,5 кН·м, 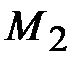 = 4 кН·м,
= 4 кН·м, 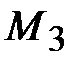 = 4,5 кН·м,
= 4,5 кН·м, 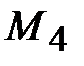 = 1 кН·м. Вид нагрузки – II, материал вала – сталь 40, напряжения [
= 1 кН·м. Вид нагрузки – II, материал вала – сталь 40, напряжения [ 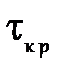 ] = 100 МПа (прил. 1).
] = 100 МПа (прил. 1).
Вычерчиваем схему вала, отмечая на ней расчетные сечения I-I, II-II, III-III и IV-IV (рис. 15, а) Определение действующих на стальной круглый вал суммарных вращающих моментов начинаем со свободного конца вала.
В сечении I-I величина суммарного вращающего момента:
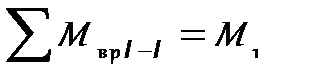 = 2,5 кН·м.
= 2,5 кН·м.
В сечении II-II величина суммарного вращающего момента:
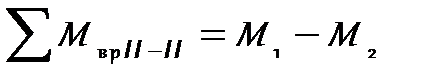 = 2,5 – 4 = – 1,5 кН·м.
= 2,5 – 4 = – 1,5 кН·м.
В сечении III-III величина суммарного вращающего момента:
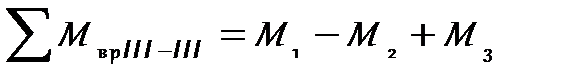 = 2,5 – 4 + 4,5 = 3 кН·м.
= 2,5 – 4 + 4,5 = 3 кН·м.
В сечении IV-IV величина суммарного вращающего момента:
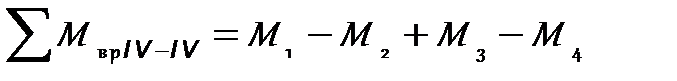 = 2,5 – 4 + 4,5 – 1 = 2 кН·м.
= 2,5 – 4 + 4,5 – 1 = 2 кН·м.
По расчетным данным строим эпюру вращающих моментов 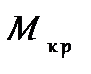 (рис. 15, б). Анализ данной эпюры показывает, что наибольший суммарный вращающий момент
(рис. 15, б). Анализ данной эпюры показывает, что наибольший суммарный вращающий момент 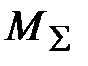 = 4,5 кН·м возникает в сечении III-III, где действует вращающий момент
= 4,5 кН·м возникает в сечении III-III, где действует вращающий момент 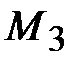 .
.
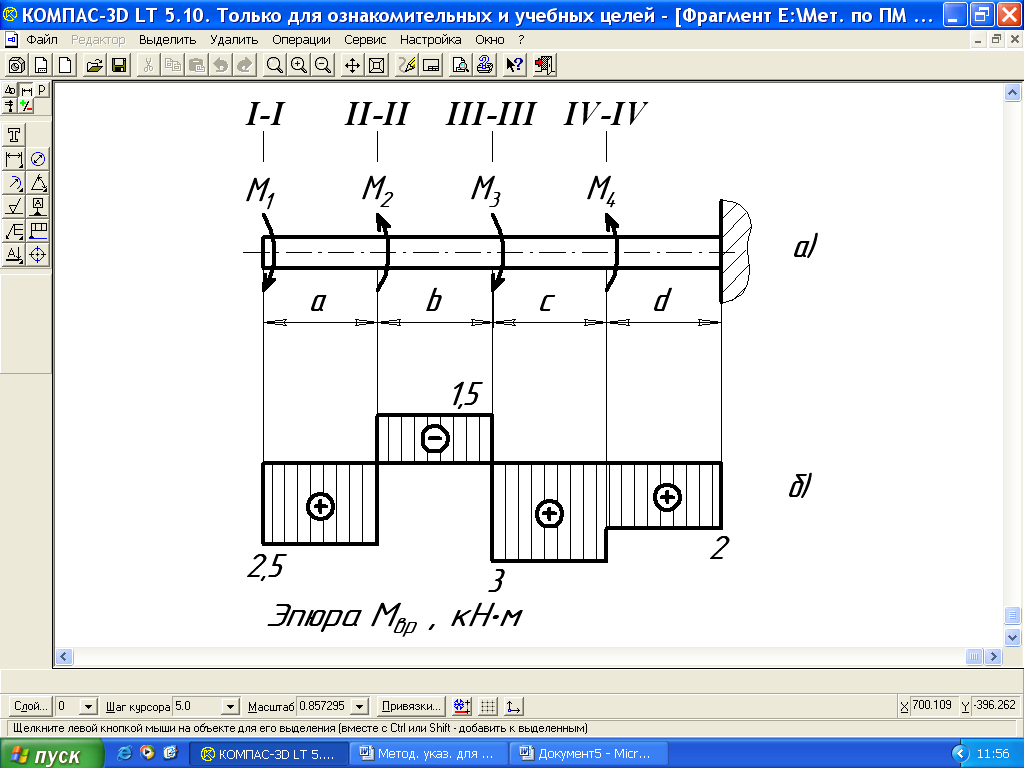
Рис. 15. Расчетная схема вала
Используя условие прочности вала, определяем диаметр вала 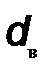 в опасном сечении (где действует наибольший суммарный вращающий момент).
в опасном сечении (где действует наибольший суммарный вращающий момент).
Условие прочности на кручение имеет вид:
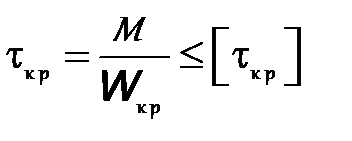 , МПа,
, МПа,
где 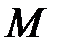 – вращающий момент, Н·мм.
– вращающий момент, Н·мм.
Момент сопротивления кручению 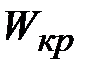 (для тел с круглым поперечным сечением, например, вал) определяется по формуле:
(для тел с круглым поперечным сечением, например, вал) определяется по формуле:
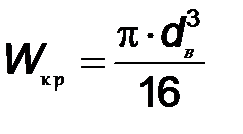 , мм 3,
, мм 3,
где 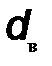 – диаметр вала, мм.
– диаметр вала, мм.
При определении допустимого диаметра вала 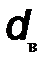 принять величину вращающего момента
принять величину вращающего момента 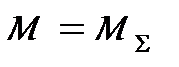 (наибольший суммарный вращающий момент, возникающий в опасном сечении, Н∙м). Расчетное значение диаметра вала необходимо округлить до целого числа.
(наибольший суммарный вращающий момент, возникающий в опасном сечении, Н∙м). Расчетное значение диаметра вала необходимо округлить до целого числа.
Задача № 3
Необходимую реакцию 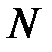 тормозной колодки на барабан определяем по зависимости:
тормозной колодки на барабан определяем по зависимости:
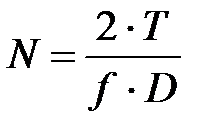 , Н,
, Н,
где 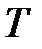 – тормозной момент на барабане, Н·м;
– тормозной момент на барабане, Н·м; 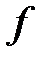 – коэффициент трения тормозной колодки о барабан;
– коэффициент трения тормозной колодки о барабан; 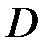 – диаметр тормозного барабана, м.
– диаметр тормозного барабана, м.
Силу натяжения тормозной ленты 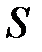 и реакцию
и реакцию 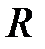 тяги рычажной системы определяем при рассмотрении расчетной схемы (рис. 16), составленной на основе расчетной схемы тормозного устройства (см. рис. 7).
тяги рычажной системы определяем при рассмотрении расчетной схемы (рис. 16), составленной на основе расчетной схемы тормозного устройства (см. рис. 7).
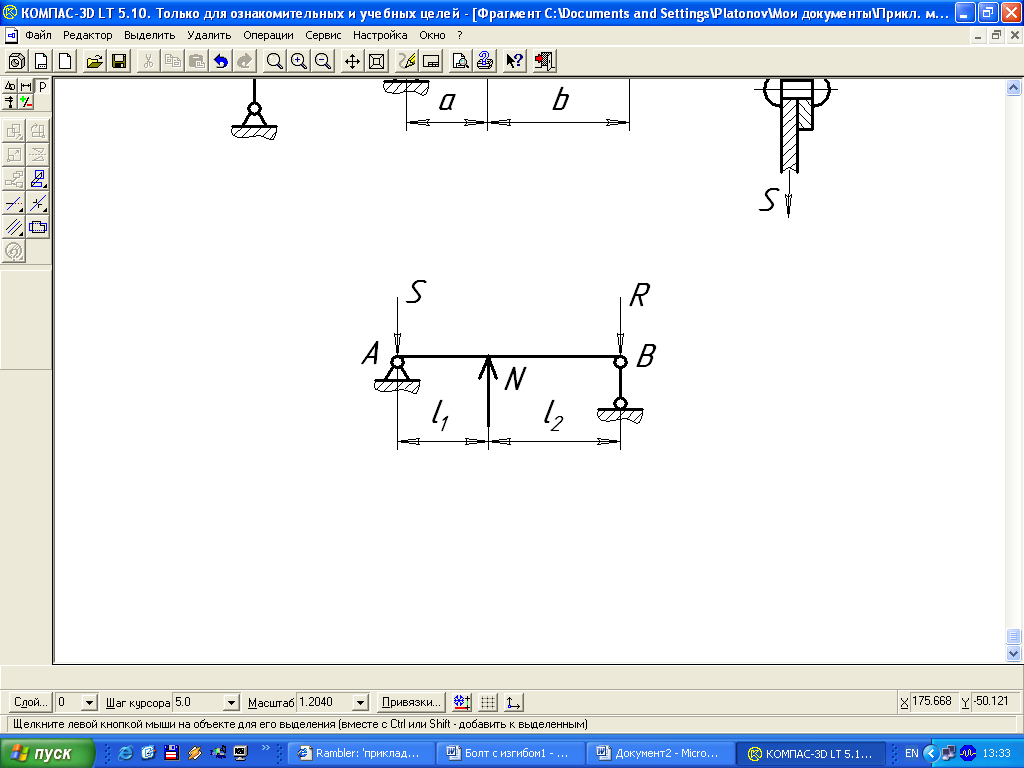 Рис. 16. Расчетная схема
Рис. 16. Расчетная схема
|
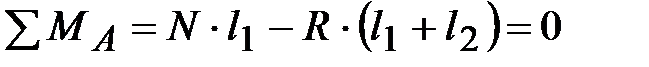 .
.
Отсюда 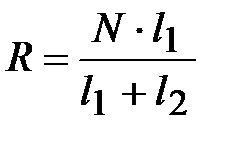 , Н.
, Н.
Составим уравнение моментов относительно опоры В (см. рис. 16):
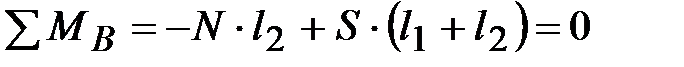 .
.
Отсюда, 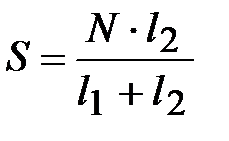 , Н.
, Н.
Для определения необходимого тормозного усилия 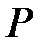 составим уравнение моментов приводного рычага (см. рис. 7):
составим уравнение моментов приводного рычага (см. рис. 7):
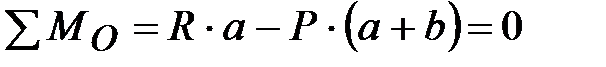 .
.
Отсюда, 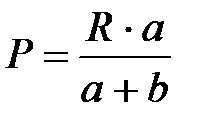 , Н.
, Н.
Возникающие в заклепочном соединении напряжения среза 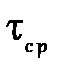 определим по условию прочности:
определим по условию прочности:
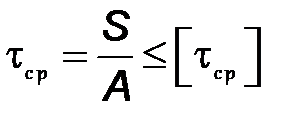 , МПа,
, МПа,
где 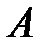 – площадь поперечного сечения одной заклепки (
– площадь поперечного сечения одной заклепки (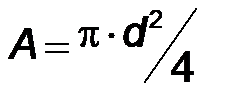 , мм 2);
, мм 2); 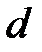 – диаметр заклепки, мм (по заданию величина диаметра заклепки известна).
– диаметр заклепки, мм (по заданию величина диаметра заклепки известна).
С учетом вышеприведенных формул, получаем:
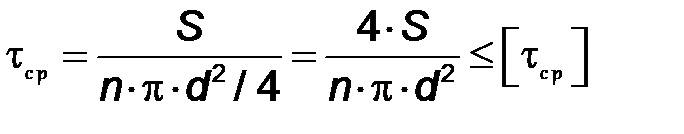 , МПа.
, МПа.
Тогда необходимое количество заклепок 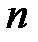 будет равно:
будет равно:
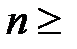
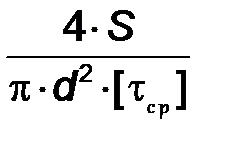 .
.
Количество заклепок 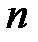 необходимо округлить до целого числа.
необходимо округлить до целого числа.
Используя условие прочности заклепок на смятие, определяем минимальную толщину тормозной ленты 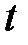 :
:
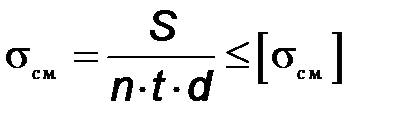 , МПа.
, МПа.
Из условия прочности тормозной ленты на разрыв (в сечении с наибольшим количеством заклепок) определяем ширину тормозной ленты 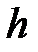 :
:
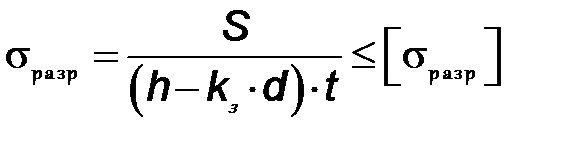 , МПа,
, МПа,
где 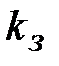 – количество заклепок в поперечном сечении ленты.
– количество заклепок в поперечном сечении ленты.
Толщину тормозной ленты 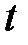 и ширину тормозной ленты
и ширину тормозной ленты 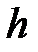 необходимо округлить до целого числа.
необходимо округлить до целого числа.
Рекомендуемая литература
Основная
1. Джамая В.В. Прикладная механика: учебник для студентов высших учебных заведений. – М.: Дрофа, 2004.
2. Скойбеда А.Т. Прикладная механика: учебник для студентов высших учебных заведений. – Минск: Выш. шк., 1997.
3. Иванов М.Н., Финогенов В.А. Детали машин: учебник для вузов. 8-е издание. – М.: Выс. шк., 2004.
4. Дунаев П.Ф., Леликов О.П. Конструирование и деталей машин: учебное пособие для технических специальностей вузов. 8-е издание. – М.: Издательский центр «Академия», 2004.
5. Саргсян А.Е. Сопротивление материалов, теории упругости и пластичности. – М.: Выс. шк., 2000.
Дополнительная
1. Иоселевич Г.Б., Строганов Г.В., Маслов Г.С. Прикладная механика. – М.: Выс. шк., 1989.
2. Белоконев И.М., Балан С.А., Белоконев К.И. Теория механизмов и машин. – М.: Дрофа, 2004.
3. Теория механизмов и механика машин / Под ред. акад. Фролова К.В. – М.: Выс. шк., 2001.
4. Мицкевич В.Г., Накапкин А.Н. Теория механизмов и машин. – М.: РГОТУПС, 2003.
5. Смелягин А.И. Теория механизмов и машин: Уч. пос. – М.: Инфа-М, 2003.
6. Битюцкий Ю.И., Мицкевич В.Г., Доль В.Д. Прикладная механика. Уч. пос. – М.: РГОТУПС, 2006.
7. Куклин Н.Г., Куклина Г.С., Житков В.К. Детали машин. – М.: Выс. шк., 2005.
Приложение 1
Значения допустимых напряжений кручения [ 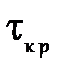 ], МПа
], МПа
| Стали | ||||
| Ст6 | ||||
Приложение 2
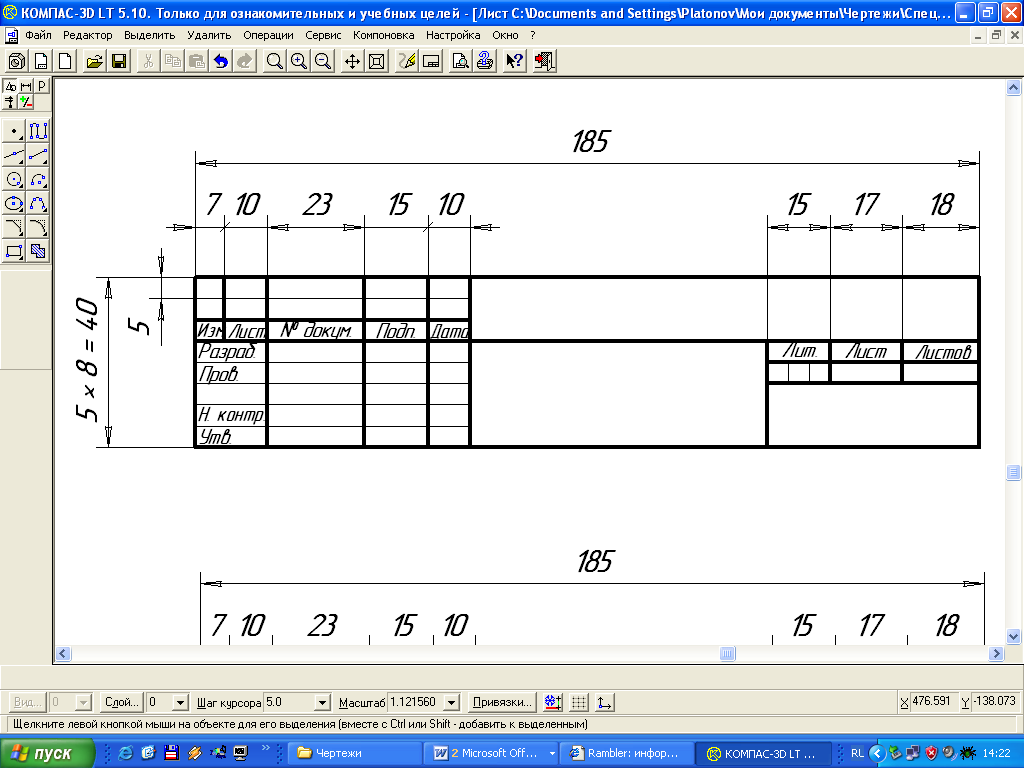
Основная надпись (форма 2)
Приложение 3
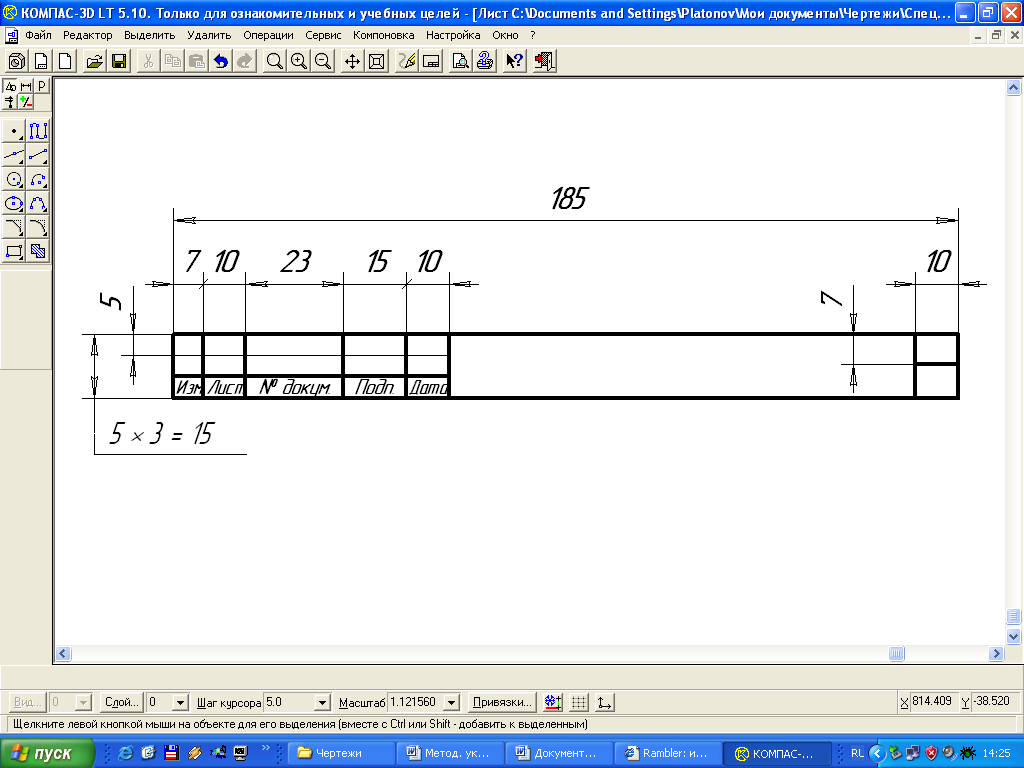
Основная надпись (форма 2а)
Приложение 4
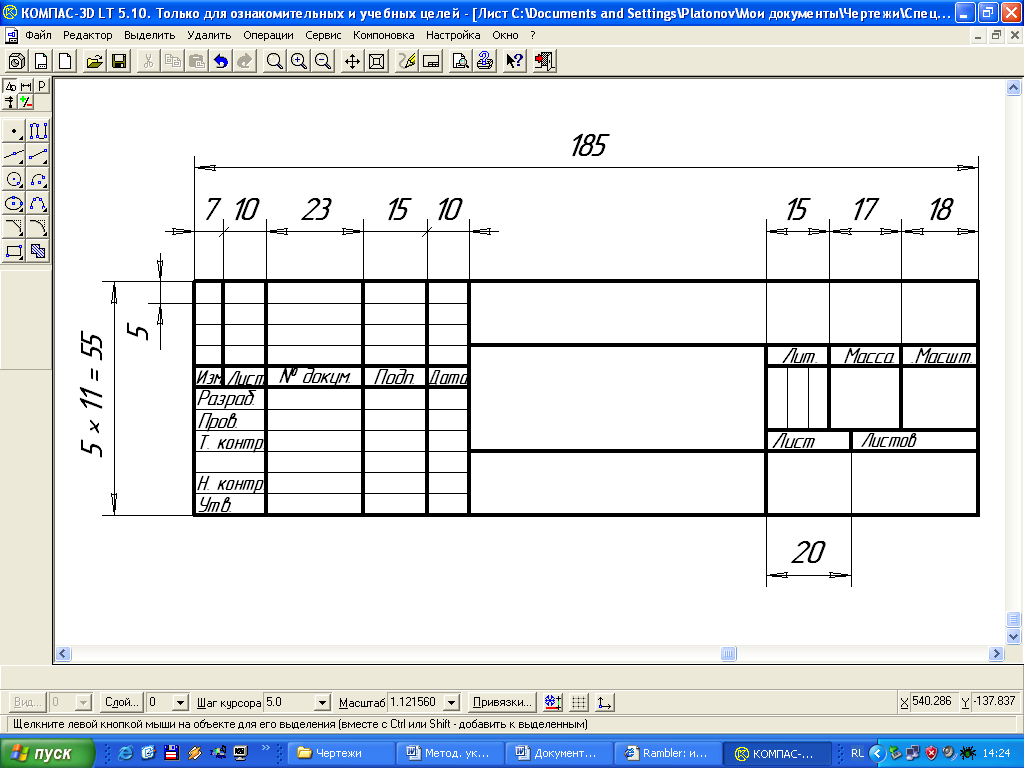
Основная надпись (форма 1)
МЕХАНИКА
Задание на контрольную работу № 1, с методическими указаниями
Редактор Д.Н. Тихонычев
Компьютерная верстка А.Ю. Байкова
| Тип. зак. Подписано в печать 12.09.08 Усл. печ. л. 8,75 | Изд. зак.147 Гарнитура Times | Тираж 1 000 экз. Офсет Формат 60×901/8 |
Издательский центр и Участок оперативной печати
Информационно-методического управления РГОТУПСа,
125993, Москва, Часовая ул., 22/2
 2017-10-31
2017-10-31 604
604
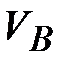 ) и скорости
) и скорости 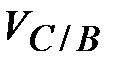 (относительного вращательного
(относительного вращательного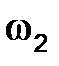 ; при этом
; при этом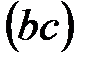 отложить отрезок
отложить отрезок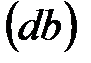 = 13,1 мм. Соединить полученную точку «
= 13,1 мм. Соединить полученную точку «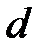 »
»






