Метод ветвей и границ. Решение задачи «о рюкзаке» методом ветвей и границ

Пусть Q – задача минимизации

S – множество допустимых решений

φ(S) – качество решения

Задача: найти S* такое, что φ(S*) – минимальное.

Метод:

Разбиваем S на подмножества 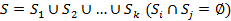. Для всех подмножеств строится оценка 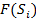такое, что 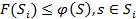. Если найдено 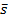такое, что 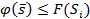, то все решения из 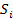рассматривать не нужно.

Задача «о рюкзаке»

Дано:

nпредметов

Веса: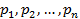

Стоимости: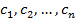

Рюкзак вместимостью V

Ограничение: .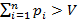

Найти:

Множество предметов M: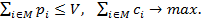

Задача является NP-полной.

1 способ:

1) Рассчитать ценность предметов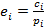

2) Упорядочить предметы по уменьшению ценности.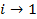

3) Ветвление (бинарное):

S₁ – 1-ый предмет берем

S₂ – 1-ый предмет не берем

4) Оценка:

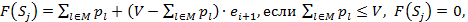иначе.

где M–множество предметов, которые уже взяли;

i+1 – номер очередного, еще не рассмотренного, предмета.

5) Выбираем вершину с максимальной оценкой, изменяем значение i и переходим к п.3

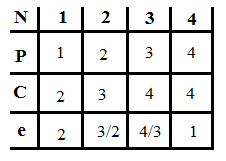
Пример:

4 предмета, V=5

Вершины графа пронумерованы сверху вниз слева направо

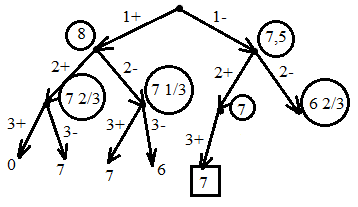
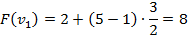
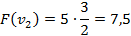
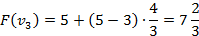
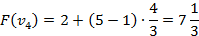
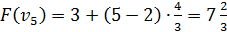
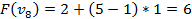
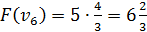
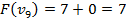
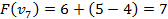
Ответ: набор {2;3}.

2 способ:

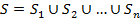
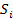- попадают все случаи, когда минимальный набор предметов, сложенных в рюкзак, равен i. На j-ом шаге ветвление аналогично, но рассматриваем не минимальный номер, а j-ый по величине.

Вершины графа пронумерованы сверху вниз слева направо

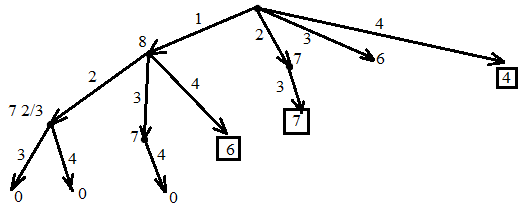
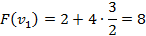
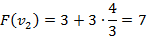
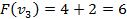
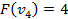
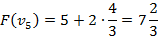
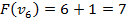
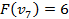
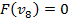
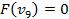
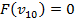
Ответ: {2,3}