Понятие линейной зависемости,независемости строк(столбцов) матрицы. Необходимое и достаточное условия линейной зависемости столбцов матрицы

Линейная независимость строк матрицы

Дана матрица 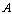размера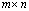

Обозначим строки матрицы следующим образом:

Две строки называются равными, если равны их соответствующие элементы. .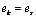

Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно:

.

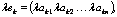
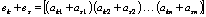Определение. Строка 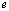называется линейной комбинацией строк 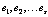матрицы, если она равна сумме произведений этих строк на произвольные действительные числа 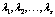(любые числа):

.

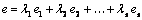Определение. Строки матрицы называются линейно зависимыми, если существует такие числа 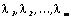, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, где 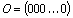. (1.1)

Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.

Определение. Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты , то строки называются линейно независимыми.