Задачі математичної фізики
При вивченні більшості фізичних явищ та процесів приходиться мати справу з тим, що їх властивості описуються диференціальними рівняннями у часткових похідних, в яких невідомими величини є функції не однієї, а декількох змінних. Аргументам таких рівнянь надають змісту просторових змінних або просторових змінних і часу.
В загальному випадку диференціальне рівняння з частковими похідними можна записати у такій формі:
 (8.1)
(8.1)
де  - постійні коефіцієнти,
- постійні коефіцієнти,
 - невідома функція, аргументи якої змінні
- невідома функція, аргументи якої змінні  і
і  , одна із яких може бути часом
, одна із яких може бути часом  , а інша, допустимо
, а інша, допустимо  , просторовою змінною;
, просторовою змінною;
 ;
;  ;
; 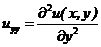 - часткові похідні другого порядку;
- часткові похідні другого порядку;
 ;
;  - часткові похідні першого порядку;
- часткові похідні першого порядку;
 - відома функція, яка враховує взаємодію фізичної системи з навколишнім середовищем.
- відома функція, яка враховує взаємодію фізичної системи з навколишнім середовищем.
Існує три типи рівнянь (8.1):
Якщо  , то рівняння (8.1) називається еліптичним;
, то рівняння (8.1) називається еліптичним;
Якщо 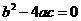 , то рівняння (8.1) буде параболічним і якщо
, то рівняння (8.1) буде параболічним і якщо  , то матимемо гіперболічне рівняння.
, то матимемо гіперболічне рівняння.
У випадку постійних коефіцієнтів при похідних другого порядку шляхом перетворення змінних рівняння (8.1) можна привести до виду, яке не вміщує змішаних похідних (b = 0). Тоді тип рівняння визначається за таким правилом: якщо у рівняння (8.1) b = 0 і постійні коефіцієнти при похідних другого порядку мають одинакові знаки в одній частині рівняння, то таке рівняння – еліптичне; якщо різні – гіперболічне; якщо похідна другого порядку за однією із змінних відсутня (b = 0; ас = 0 при  ) – параболічне.
) – параболічне.
Еліптичні рівняння
Як приклади еліптичних рівнянь у часткових похідних можна навести рівняння Лапласа, Пуассона і Гельмгольца.
Якщо ввести оператор Лапласа  функції
функції  , то в загальному вигляді можна записати
, то в загальному вигляді можна записати
 - рівняння Лапласа;
- рівняння Лапласа;
 - рівняння Пуассона;
- рівняння Пуассона;
 - рівняння Гельмгольца,
- рівняння Гельмгольца,
де  ,
,  - задані функції, зміст яких визначається задачею, що розв’язується.
- задані функції, зміст яких визначається задачею, що розв’язується.
У рівняннях Лапласа, Пуасона, Гельмгольца одна із мінних може бути як просторовою координатою, так і часом  .
.
Рівняння Лапласа використовують для математичного опису електромагнітних полів, магнітних полів постійного струму, стаціонарних теплових полів.
Області застосування рівнянь Пуассона – задачі електростатики, електронної оптики, теорії пружності та ін.
Рівняння Гельмгольца є математичною моделлю коливних процесів, наприклад, в акустиці.
Допустимо, що розв’язок еліптичного рівняння належить області Ω з границею Г. Розглянемо найпростіший випадок, коли Ω - прямокутник [ a, b ] x [ c, d ].
Двовимірну область W накриємо сіткою вузлів з координатами  (рис 8.1), де
(рис 8.1), де 
 ,
,  ;
;  ,
,  ,
,  ,
,
 - кількість вузлів розбиття;
- кількість вузлів розбиття;  - кроки та сітці.
- кроки та сітці.

Рисунок 8.1 –Сітка для дискретизації задачі
Вузли  називають внутрішніми, коли
називають внутрішніми, коли  ,
,  і граничними, коли
і граничними, коли  або
або  та
та  або
або  , тобто
, тобто  ,
,  ,
,
 , (8.2)
, (8.2)
 ,
,  ,
,  .
.
Виразимо оператор Лапласа у дискретному вигляді, скориставшись формулою для обчислення наближення до другої похідної
 . (8.3)
. (8.3)
У відповідності з формулою (8.3) будемо мати
 (8.4)
(8.4)
і відповідно
 . (8.5)
. (8.5)
Якщо  - розрахункова точка, то
- розрахункова точка, то  і відповідно
і відповідно  ,
,  ,
,  ,
,  ,
,
де  .
.
Аналогічно  ,
,  ,
, 
Отже, в розрахунковій точці  часткові похідні
часткові похідні  і
і  можна замінити такими різницевими рівняннями:
можна замінити такими різницевими рівняннями:
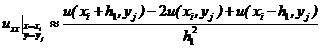 ,
,
 .
.
Переходячи до прийнятих позначень, отримаємо
 , (8.6)
, (8.6)
 . (8.7)
. (8.7)
Таким чином,
 . (8.8)
. (8.8)
Різницеве рівняння (8.8) можна спростити, якщо крок сітки зробити постійним як за змінною  , так за змінною
, так за змінною  тобто
тобто  .
.
Тоді
 . (8.9)
. (8.9)
Допустимо, що числовим методом необхідно розв’язати диференціальне рівняння з частковими похідними другого порядку, яке є еліптичним рівнянням
 , (8.10)
, (8.10)
де  - задана функція, а W - прямокутник. Тоді у відповідності з (8.8) запишемо дискретний аналог еліптичного рівняння
- задана функція, а W - прямокутник. Тоді у відповідності з (8.8) запишемо дискретний аналог еліптичного рівняння
 . (8.11)
. (8.11)
Рівняння (8.10 необхідно доповнити сукупністю граничних умов (8.2) на Г.
Розглянемо техніку обчислення значень функції  у вузлах решітки W Розглянемо перших три шари решітки (рис 8.2). Зафіксуємо значення j. Візьмемо j =1.
у вузлах решітки W Розглянемо перших три шари решітки (рис 8.2). Зафіксуємо значення j. Візьмемо j =1.
Тоді при  із (8.11) отримаємо рівняння
із (8.11) отримаємо рівняння
 .
.
Якщо тепер  змінювати від 2 до
змінювати від 2 до 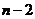 , то
, то
 ,
,  .
.
І, нарешті, при  будемо мати
будемо мати
 ,
,
де  .
.

Рисунок 8.2-Перші три шари решітки W
Тепер можна взяти j =2 і знову скласти систему із n -1 рівнянь. Повторюючи процес складання рівнянь для  , отримаємо систему із
, отримаємо систему із  рівнянь в якій
рівнянь в якій  невідомих.
невідомих.
Сказане проілюструємо конкретним прикладом.
Приклад 8.1. Знайдемо наближений розв’язок еліптичного рівняння  у прямокутнику
у прямокутнику  де
де  - температура у точці (x,y), а граничні умови наступні:
- температура у точці (x,y), а граничні умови наступні:
 для
для  ,
,
 для
для  .
.
Виберемо крок сітки  знайдемо кількість вузлів сітки: в напрямку
знайдемо кількість вузлів сітки: в напрямку 
 ; у напрямку
; у напрямку 
 .
.
Сітка W показана на рис 8.3

Рисунок 8.3 – Сітка W для n = m =5
Складемо систему алгебраїчних рівнянь використавши формулу (8.11) в якій  , а
, а  . Маємо
. Маємо
 . (8.12)
. (8.12)
Змінюючи індекси  та j від 1 до 3 отримаємо систему із дев’яти рівнянь
та j від 1 до 3 отримаємо систему із дев’яти рівнянь


 ,
,
 ,
,
 ;
;

 ,
,
 ,
,
 ,
,
 ;
;

 ,
,
 ,
,
 .
.
Отриману систему рівнянь можна записати у матрично векторній формі
 , (8.13)
, (8.13)
де
 ,
,  ,
, 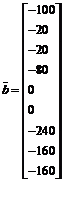
Відмітимо, що при складанні системи рівнянь зручно використовувати шаблон типу “хрест” (рис 8.4). Першою у рівнянні (8.11) записується змінна  другою
другою  , третьою
, третьою  з коефіцієнтом мінус чотири, четвертю
з коефіцієнтом мінус чотири, четвертю 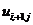 і п’ятою
і п’ятою  .
.

Рисунок 8.4-Шаблон типу “хрест”
У тому випадку, коли у процесі складання рівнянь шаблон вміщує граничні точки, то значення відповідних змінних  та
та  , які відповідають таким точкам, переносяться у праву частину рівнянь (8.11).
, які відповідають таким точкам, переносяться у праву частину рівнянь (8.11).
Для розв’язування отриманої системи рівнянь (8.13) скористаємося процедурою SystemEqualizationAgebra (роділ 6). У результаті розв’язку отримані такі значення компонентів вектора:  Графік зміни температурного поля в координатах
Графік зміни температурного поля в координатах  показаний на рис 8.5.
показаний на рис 8.5.
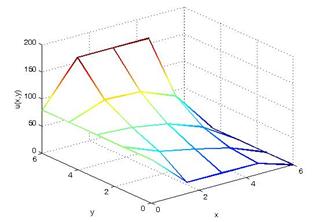
Рисунок 8.5 –графік зміни температури у вузлових точках функції 
Таким чином, задачу розв’язку еліптичних рівнянь ми апроксимували дискретною задачею, яка має другий порядок точності і яка має однозначне рішення. Це рішення збігається до рішення з початкової задачі при нескінченному згущенні вузлів сітки за двома змінними одночасно.
Параболічні рівняння
Як приклад параболічного рівняння розглянемо рівняння теплопровідності
 ,
, 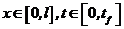 (8.14)
(8.14)
з початковими умовами за змінною 
 при
при  (8.15)
(8.15)
і крайовими умовами за просторовою координатою х
 ,
,  , при
, при 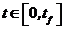 (8.16)
(8.16)
Рівняння (8.14) можна інтерпретувати як задачу визначення температури  тонкого однорідного стержня (бруса) довжиною l, якщо відомий розподіл температури в стержні у початковий момент часу t= 0(початкова умова (8.15))і відома зміна температури на кінцях стержня х= 0 і х=l у будь-який момент часу t (граничні умови (8.16)) Коефіцієнт а2 в (8.14) визначається теплофізичними властивостями матеріалу, а функція g(t,x) виражає дію зовнішнього теплового джерела на стержень і вважається заданою.
тонкого однорідного стержня (бруса) довжиною l, якщо відомий розподіл температури в стержні у початковий момент часу t= 0(початкова умова (8.15))і відома зміна температури на кінцях стержня х= 0 і х=l у будь-який момент часу t (граничні умови (8.16)) Коефіцієнт а2 в (8.14) визначається теплофізичними властивостями матеріалу, а функція g(t,x) виражає дію зовнішнього теплового джерела на стержень і вважається заданою.
Із умов (8.15) і (8.16) видно, що область W - прямокутник зі сторонами  у системі координат
у системі координат  , а її границя
, а її границя  утворена відрізками прямих
утворена відрізками прямих  ,
,  ,
,  і
і  . Як і раніше розіб’ємо прямокутник на
. Як і раніше розіб’ємо прямокутник на  прямокутників зі сторонами
прямокутників зі сторонами  і
і  , тобто
, тобто
 , (8.17)
, (8.17)
 . (8.18)
. (8.18)
Значення функції  у вузлах
у вузлах 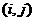 позначимо через
позначимо через  (рис 8.6) Аналогічне позначення введемо і для функції
(рис 8.6) Аналогічне позначення введемо і для функції 
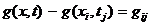 .
.

Рисунок 8.6 – Сітка області W
Часткові похідні  і
і  замінимо різницевими апроксимаціями першого порядку
замінимо різницевими апроксимаціями першого порядку
 ,
,
 .
.
Оскільки (див. рис. 8.6) 
 ,
,  , то
, то
 , (8.19)
, (8.19)
 . (8.20)
. (8.20)
Замінюючи в рівнянні (8.14) часткові похідні  і
і  їх апроксимаціями (8.16) і (8.17).
їх апроксимаціями (8.16) і (8.17).
Отримаємо наступне рівняння
 ,
,
 ,
, 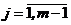 , (8.21)
, (8.21)
де  .
.
До рівнянь (8.21) слід добавити початкові та граничні умови, які отримаємо шляхом апроксимації функції умов (8.15) і (8.16). Маємо

 , (8.22)
, (8.22)
 (8.23)
(8.23)
Якщо індекси i та j в (8.21) будуть набувати значень від 1 до n -1 і від 1 до m -1 відповідно, то в результаті отримаємо систему (n -2)(m -2) алгебраїчних лінійних рівнянь з (n -2)(m -2) невідомими. Складання такої системи рівнянь опирається на шаблон різницевої схеми (8.18) (рис 8.7).

Рисунок 8.7 Шаблон різницевої схеми (8.21)
Апроксимація рівняння (8.14) різницевою схемою (8.21) може привести до того, що обчислювальний процес стає нестійкий. Це означає, що помилки, які виникають на одному шарі можуть збільшуватись на наступних парах для деякою  . Для того щоб отримати стійку схему обчислень розмір кроку
. Для того щоб отримати стійку схему обчислень розмір кроку  повинен підкорятись нерівності
повинен підкорятись нерівності  .
.
Інший спосіб отримання різницевої схеми, яка апроксимує параболічне рівняння (8.14) полягає в апроксимації першої похідної лівою різницею
 . (8.24)
. (8.24)
Після заміни другої і першої похідних в (8.14) їх апроксимаціями (8.20) і (8.24) отримаємо

Звідси знаходимо, що
 . (8.25)
. (8.25)
Зміні, які входять у різницеву схему (8.25), утворюють шаблон, який показаний на рис. 8.8.

Рисунок 8.8 – Шаблон для різницевої схеми (8.25)
Структура системи рівнянь (8.25) така, що значення невідомих  можна обчислювати для кожного шару окремо. Враховуючи, що на нульовому шарі значення
можна обчислювати для кожного шару окремо. Враховуючи, що на нульовому шарі значення  відомі, формула (8.25) дає можливість безпосередньо обчислювати всі значення
відомі, формула (8.25) дає можливість безпосередньо обчислювати всі значення  для першого шару. Знаючи значення
для першого шару. Знаючи значення  першого шару, можна обчислити значення
першого шару, можна обчислити значення  для другого шару і т.д.
для другого шару і т.д.
Отже, для знаходження значень  у вузлах першого шару необхідно розв’язати систему лінійних алгебраїчних рівнянь
у вузлах першого шару необхідно розв’язати систему лінійних алгебраїчних рівнянь
 ,
,
де 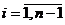 ,
,  ,
,  .
.
Значення величин  у вузлових точках другого шару отримаємо як розв’язок системи
у вузлових точках другого шару отримаємо як розв’язок системи
 ,
,
де 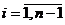 ,
, 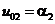 ,
,  , і т. д.
, і т. д.
Для передостаннього шару, коли  , будемо мати
, будемо мати
 .
.
У кожній із двох розглянутих різницевих схем (8.21) і (8.25) для обчислення значень 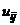 на і -ому шарі використовуються значення функції
на і -ому шарі використовуються значення функції 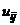 , на двох сусідніх шарах. Звідси і їх назва – двошарові схеми.
, на двох сусідніх шарах. Звідси і їх назва – двошарові схеми.
При цьому різницева схема (8.21), яка є формулою для безпосереднього обчислення шуканих значень 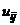 носить назву – явної схеми, а схема (8.25), яка для своєї реалізації вимагає розв’язку систем алгебраїчних рівнянь (при переході від шару до шару) називається неявною схемою.
носить назву – явної схеми, а схема (8.25), яка для своєї реалізації вимагає розв’язку систем алгебраїчних рівнянь (при переході від шару до шару) називається неявною схемою.
Приклад 8.2. Розв’язати числовим методом параболічне рівняння  , коли відсутня дія зовнішнього джерела тепла, тобто
, коли відсутня дія зовнішнього джерела тепла, тобто  .
.
Шляхом вибору безрозмірних величин:  і
і  рівняння (8.14) можна привести до вигляду, у якому коефіцієнт при частковій похідні
рівняння (8.14) можна привести до вигляду, у якому коефіцієнт при частковій похідні 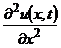 буде дорівнювати одиниці.
буде дорівнювати одиниці.
Оскільки  і
і  , то
, то 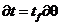 і
і  . Підставляючи значення
. Підставляючи значення  і
і  у рівняння (8.14), отримаємо
у рівняння (8.14), отримаємо
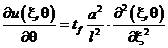 . (8.26)
. (8.26)
Виберемо масштаб часу  таким, щоб коефіцієнт
таким, щоб коефіцієнт  у рівнянні (8.26) був рівний одиниці, тобто
у рівнянні (8.26) був рівний одиниці, тобто
 .
.
При такому виборі  рівняння (8.26) набуде такого вигляду:
рівняння (8.26) набуде такого вигляду:
 . (8.27)
. (8.27)
з початковою умовою
 для
для  і
і  (8.28)
(8.28)
і граничними умовами
 , для
, для 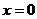 і
і  ,
,
 , для
, для  і
і  , (8.29)
, (8.29)
де  .
.
Графік розподілу температури вздовж стержня в початковий момент часу показано на рис.8.9.

Рисунок 8.9 – Розподіл температури вздовж стержня у початковий момент часу
Крок дискретності  виберемо таким, щоб виконувалась умова
виберемо таким, щоб виконувалась умова  . Візьмемо
. Візьмемо  .
.
Інтервал зміни  розіб’ємо на
розіб’ємо на 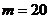 частин. Тоді
частин. Тоді  , а
, а  і відповідно
і відповідно  .
.
Для розв’язку задачі (8.27) з початковою умовою (8.28) і граничними умовами (8.29) використаємо явну різницеву схему (8.21). Відповідне алгоритмічне забезпечення має назву EqualizationHeat-conducting, де індексація починається не з нуля, а з одиниці тому в (8.21) індекс 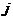 замінимо на
замінимо на 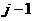 . У результаті отримаємо
. У результаті отримаємо
 , (8.30)
, (8.30)
де  .
.
EqualizationHeat-conducting
 Процедура розв'язку рівняння теплопровідності
Процедура розв'язку рівняння теплопровідності
 Вхід:fi(x)-заноситься у підпроцедуру run_fiX
Вхід:fi(x)-заноситься у підпроцедуру run_fiX
 alfa(t)=u(0,t)i beta(t)=u(l,t)
alfa(t)=u(0,t)i beta(t)=u(l,t)
 l i tk - праві точки інтервалів [0;l] i [0;tk]
l i tk - праві точки інтервалів [0;l] i [0;tk]
 a-постійна у рівнянні теплопровідності
a-постійна у рівнянні теплопровідності
 n i m-число точок решітки [0;l] i [0;tk]
n i m-число точок решітки [0;l] i [0;tk]
 Вихід:U-матриця розв'язків
Вихід:U-матриця розв'язків
 Вхідні дані
Вхідні дані
1 l=1
2 tk=0.5
3 c1=0
4 c2=0
5 a=1
6 m=80;
7 n=21
 Кроки tau і h на решітці
Кроки tau і h на решітці
8 h=1/(n-1)
9 tau=tk/(m-1)
 Параметри рівняння та ініціалізація U
Параметри рівняння та ініціалізація U
9 gama=tau*a^2/h^2;
10 gama_1=1-2*gama;
11 Створити нульову матрицю U розміром nxm
12 Створити нульовий вектор fi розміром n-2
 Граничні умови
Граничні умови
13 U(1,1:m)=c1
14 U(n,1:m)=c2;
 Генерування значень функції u(x,t) другого рядка
Генерування значень функції u(x,t) другого рядка
15 x=0
16 for i=2 to n-1
17 x=x+h
18 fi=fun_fiX(x)
19 U(i,1)=fi
20 end for
21 for i=1 to n
22 X(i)=(i-1)*h
23 F(i)=fun_fiX(X(i))
24 end for
25 Побудувати графік розподілу температури вздовж стержня у
початковий момент часу в координатах F,X
 Генерування значень функції u(x,t) наступних рядків
Генерування значень функції u(x,t) наступних рядків
26 for j=2 to m
27 for i=2 to n-1
28 U(i,j)=gama_1*U(i,j-1)+gama*(U(i-1,j-1)+U(i+1,j-1))
29 end for
30 end for
31 Побудувати графік функції у координатах x,y,U
Підпроцедура fun_fiX
fi=fun_fiX(x)
 Функція, що задає початкові умови fi(x)
Функція, що задає початкові умови fi(x)
fi=4*x*(1-x)
Результати роботи програми відображені на рис. 8.10.

Рисунок 8.10 - Графік функції 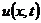
 2018-01-08
2018-01-08 438
438







