Як приклад гіперболічного рівняння розглянемо математичну модель вільних коливань струни
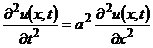 , (8.31)
, (8.31)
кінці якої зафіксовані у точках х = 0 і х = l. У початковий момент часу кожній точці струни придали початкове зміщення 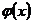 і швидкість
і швидкість 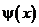 .Постійна
.Постійна 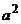 у рівняння (8.31) визначається вагою і натягом струни.
у рівняння (8.31) визначається вагою і натягом струни.
Отже, процес коливань струни визначається такими початковими
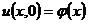 при
при 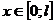 , (8.32)
, (8.32)
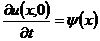 , при
, при 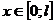 (8.33)
(8.33)
і граничними
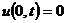 ,
, 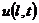 =0 при
=0 при 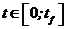 (8.34)
(8.34)
умовами.
Задача (8.32) – (8.33) визначена на прямокутній області 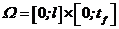 , яка є ідентичною для задачі про теплопровідність і тому для побудови різницевої схеми доцільно використати ті ж вузли, що і раніше (див. п. 8.3).
, яка є ідентичною для задачі про теплопровідність і тому для побудови різницевої схеми доцільно використати ті ж вузли, що і раніше (див. п. 8.3).
Часткові похідні другого порядку будемо апроксимувати за відомими нам формулами:
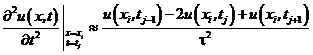 , (8.35)
, (8.35)
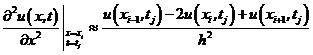 . (8.36)
. (8.36)
Замінивши у (8.31) часткові похідні 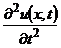 і
і 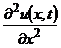 їх наближеннями (8.35) і (8.36), отримаємо різницеву схему
їх наближеннями (8.35) і (8.36), отримаємо різницеву схему
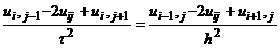 ,
,
яка апроксимує хвильове рівняння (8.31) на шаблоні типу «хрест» (рис.8.4).
Якщо ввести позначення 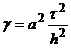 , то
, то
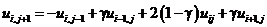 , (8.37)
, (8.37)
де 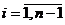 ,
, 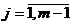 .
.
Відповідним чином видозмінюється початкова (8.32)
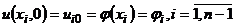 (8.38)
(8.38)
і гранична (8.34)
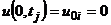 ,
, 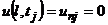 ,
, 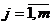 (8.39)
(8.39)
умови.
Оскільки кінці струни зафіксовані у точках 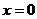 і
і 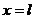 , то
, то 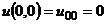 і
і 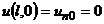 .
.
Початкова умова (8.33) задана у диференціальній формі, що вимагає, застосування до неї форм апроксимації. Найпростіша із них
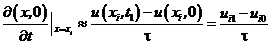 .
.
Тоді у відповідності з (8.33) 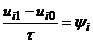 або
або
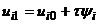 . (8.40)
. (8.40)
У тому випадку, коли функція 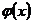 має другу похідну, можна скористатися формулою Тейлора порядку два, щоб обчислити значення
має другу похідну, можна скористатися формулою Тейлора порядку два, щоб обчислити значення 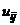 для другого ряду.
для другого ряду.
Оскільки 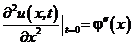 . У відповідності з рівнянням (8.31)
. У відповідності з рівнянням (8.31) 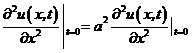
.
Отже,
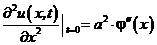 (8.41)
(8.41)
Розкладемо функцію 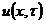 у ряд Тейлора порядку два. Маємо
у ряд Тейлора порядку два. Маємо
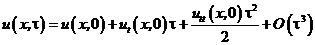 ,
,
де 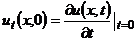 ;
; 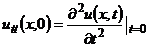 ;
;
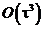 - залишковий член ряду Тейлора.
- залишковий член ряду Тейлора.
Оскільки, у відповідності з формулою (8.33) 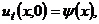 а згідно (8.40)
а згідно (8.40) 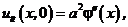 то
то
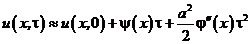 . (8.42)
. (8.42)
Формулу (8.42) можна застосувати для обчислення значень 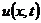 для першого ряду. Для цього візьмемо
для першого ряду. Для цього візьмемо 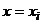 ,
, 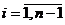 , а функції
, а функції 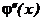 апроксимуємо за формулою
апроксимуємо за формулою
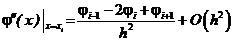 , (8.43)
, (8.43)
де 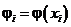 .
.
Так як 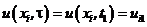 , то формули (8.42) і (8.43) дають можливість записати наступну формулу для дискретних значень
, то формули (8.42) і (8.43) дають можливість записати наступну формулу для дискретних значень 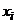 :
: 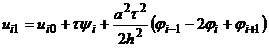 .
.
Оскільки 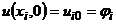 ,
,
то 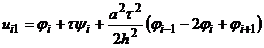 .
.
Якщо врахувати, що 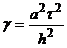 , то
, то
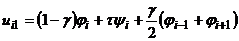 . (8.44)
. (8.44)
На відміну від формули (8.37), яка забезпечує перший порядок точності 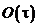 , формула (8.40) має другий порядок точності
, формула (8.40) має другий порядок точності 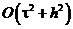 .
.
Доказано*, що умова 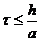 забезпечує стійкість обчислювального процесу за різницевою схемою (8.37).
забезпечує стійкість обчислювального процесу за різницевою схемою (8.37).
Приклад 8.3. Задано хвильове рівняння
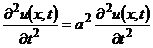 ,
, 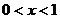 і
і 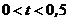 ,
,
де а = 2, з граничними умовами
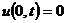 ,
, 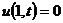 для
для 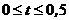 ,
,
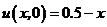 , для
, для 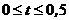 ,
,
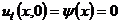 для
для 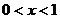 .
.
Знайти його розв’язок числовим методом. Виберемо 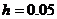 . Для стійкого обчислювального процесу повинна виконуватись умова
. Для стійкого обчислювального процесу повинна виконуватись умова 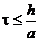 . Візьмемо
. Візьмемо 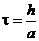 . Оскільки
. Оскільки 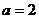 , то
, то 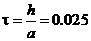 . Отже, кількість точок для дискретних значень х -
. Отже, кількість точок для дискретних значень х - 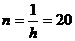 , а для дискретних значень
, а для дискретних значень 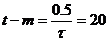 .
.
Обчислення значень функції 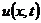 у вузлах
у вузлах 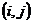 будемо здійснювати за формулою (8.37). значення
будемо здійснювати за формулою (8.37). значення 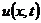 для нульового ряду обчислюється за формулою (8.38), а для першого ряду – за (8.44).
для нульового ряду обчислюється за формулою (8.38), а для першого ряду – за (8.44).
Процедура HyperbolicEqualization знаходить наближений розв’язок хвильового рівняння (8.31) за різницевою схемою (8.37).
HyperbolicEqualization
 Розв'язок хвильового рівняння (гіперболічного)
Розв'язок хвильового рівняння (гіперболічного)
 Вхід:fi(x)-визначається підпроцедурою run_fiG
Вхід:fi(x)-визначається підпроцедурою run_fiG
 psi(x)- визначається підпроцедурою run_psiG
psi(x)- визначається підпроцедурою run_psiG
 l i tk - праві точки інтервалів [0;l] i [0;tk]
l i tk - праві точки інтервалів [0;l] i [0;tk]
 a-постійна у хвильовому рівнянні
a-постійна у хвильовому рівнянні
 n i m-число точок решітки [0;l] i [0;tk]
n i m-число точок решітки [0;l] i [0;tk]
 Вихід:U-матриця розв'язків
Вихід:U-матриця розв'язків
 Вхідні дані
Вхідні дані
1 l=1
2 tk=0.5
3 a=2
4 m=21
5 n=21
 Кроки tau і h на решітці
Кроки tau і h на решітці
6 h=1/(n-1)
7 tau=tk/(m-1)
 Параметри рівняння та ініціалізація U
Параметри рівняння та ініціалізація U
8 gama=tau^2*a^2/h^2
9 Створити нульову матрицю U розміром nxm
 Генерування значень функції u(x,t) першого і другого рядів
Генерування значень функції u(x,t) першого і другого рядів
10 for i=2 to n-1
11 fi_1=fun_fiG(h*(i-1))
12 fi=fun_fiG(h*i)
13 fi_2=fun_fiG(h*(i-2))
14 psi_1=fun_psiG(h*(i-1))
15 U(i,1)=fi_1
16 U(i,2)=(1-gama)*fi_1+tau*psi_1+gama*(fi+fi_2)/2
17 end for
 Генерування значень функції u(x,t) наступних рядків
Генерування значень функції u(x,t) наступних рядків
18 for j=3 to m
19 for i=2 to n-1
20 U(i,j)=2*(1-gama)*U(i,j-1)+gama*(U(i-1,j-1)+...
21 U(i+1,j-1))-U(i,j-2)
22 end for
23 end ror
24 Побудувати графік функції у координатах x,y,U
 2018-01-08
2018-01-08 344
344








