Теоретические сведения. Общий алгоритм симплекс-метода следующий

Общий алгоритм симплекс-метода следующий:

1. Находится любое базисное решение;

2. Проверяется условие максимума целевой функции в данной точке. Если максимум не достигнут, то переходим к следующей точке, но только уже к той, которая приближает к экстремуму. Повторяем этот шаг до тех пор, пока не будет достигнут экстремум функции.

6.1.1 Табличный симплекс-метод

Достоинством данного метода является то, что он хорошо реализуется программно.

Поскольку система уравнений ограничений для задачи в каноническом виде является линейно независимой, то переменную, входящую в некоторое уравнение с нулевым коэффициентом можно выразить следующим образом:

,

,

,

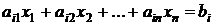. (6.1)

Имея n переменных и m < n уравнений можно выразить m базисных переменных через n - m свободных. Тогда, в общем виде задача математического программирования будет выглядеть как.

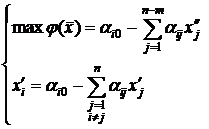, (6.2)

где – базисная переменная;. – свободная переменная.

Используя выражения (6.2) задачу можно представить в виде таблицы:

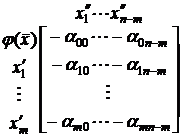. (6.3)

В матрице (6.3) записаны коэффициенты со знаком минус. Табличный метод основан на пересчете коэффициентов матрицы (6.3). По виду этих коэффициентов можно судить о том, является ли базис оптимальным, т.е. достигнут ли экстремум функции, а также о том, является ли базис допустимым, а именно:

1. Поскольку свободные переменные равны нулю, то при выделенном базисе , если коэффициенты первого столбца , больше или равны нулю, то базис является допустимым;

2. По виду коэффициентов первой строки можно судить, достигнут ли экстремум целевой функции. Экстремум достигнут, если

3. Если экстремум достигнут, то .

6.1.2 Алгоритм табличного симплекс-метода

1. Записываем начальную таблицу коэффициентов, соответствующей задачи ЛП с допустимым начальным базисом, т.е. . Свободные переменные в таблице учитываем со знаком минус. В этом случае анализируем коэффициенты первой строки, которые относятся к целевой функции. Если все , то получено оптимальное решение при решении задачи на максимум. Более того, если в строке целевой функции нет нулевых элементов, то решение единственное. Если имеется хотя бы один нулевой элемент, то решений бесчисленное множество. Если есть отрицательный элемент, то решение может быть улучшено;

2. Определяем направляющий столбец, соответствующий той свободной переменной, которую нужно перевести в базис для увеличения значения целевой функции. Выбирается столбец с наибольшим по модулю отрицательным элементом. Если таких несколько, то выбираем любой. Если в выбранном столбце все , то задача не имеет решения (допустимая область не ограничена в направлении экстремума). Если найдется положительный элемент в направляющем столбце или их будет несколько, то выбирается направляющая строка, соответствующая переменной, выводимой из базиса;

3. Выберем направляющую строку, которая удовлетворяет следующему условию

. (6.4)

В итоге выберем r -тую строку, на пересечении с которой находится разрешающий элемент ;

4. Произведем замену выбранной базисной переменной (соответствующую направляющей строке) на выбранную свободную переменную (соответствующую направляющему столбцу), при этом произведем пересчет коэффициентов матрицы по правилу Жордановых преобразований:

Ÿ разрешающий элемент заменяем на обратный ему;

Ÿ все коэффициенты направляющей строки делим на разрешающий элемент;

Ÿ все коэффициенты направляющего столбца дели на разрешающий элемент и изменяем их знак на противоположный;

Ÿ остальные коэффициенты пересчитываются по формуле:

; (6.5)

Ÿ переходим к первому пункту алгоритма для анализа новой матрицы коэффициентов.

Таким образом, алгоритм табличного симплекс-метода предусматривает итерационное повторение шагов.

К примеру, необходимонайти при ограничениях

.

Решение задачи представлено таблицами ниже.

 

		-X4	-X5
j		2/3	1/3
X3
X1		1/3	2/3
X2		-1/3	1/3

Ответ: .

6.1.3 Условие вырожденности

Если при решении задачи алгоритм зациклится, то она вырожденная. Это задача, содержащая базисное решение, в котором хотя бы одна из базисных переменных принимает нулевое значение. Такое может случиться, когда при определении направляющей строки окажется, что несколько строк имеют одинаковое симплекс-отношение. Если в этом случае выполнить пункты алгоритма 1 - 2, то задача имеет либо одно решение, либо не имеет такового вообще. Если требуется улучшение плана, то необходимо выбрать направляющую строку по минимальному симплексному отношению, а она будет соответствовать минимальному значению 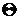, а именно нулю. Тогда в базис вводится новая переменная

. (6.6)

Значение всех остальных переменных также не изменяется. А это будет означать, что значение целевой функции также не изменяется и что очередной шаг итерации сделан вхолостую. Поскольку количество переменных ограничено, то в конце концов может быть получено условие окончания работы алгоритма для какого-то базиса. Но может оказаться, что мы вернемся к исходному базису. В этом случае задача зациклится. Для устранения зацикливания при появлении строк с минимальным симплексным отношением для элементов первого столбца необходимо проанализировать дополнительно симплексное отношение для элементов второго столбца, чтобы выбрать направляющую строку.

6.1.4 Постановка, типы, свойства транспортных задач

Формулировка транспортной задачи выглядит следующим образом. Имеется n пунктов отправления, в каждом из которых имеется груз а₁, …, а_n и b₁, …, b_n пунктов приема. с₁, …, с_n – стоимости перевозки. .

, (6.7)

(6.8)

Здесь x_ij – количество груза, перевозимого из a_i в b_j. Матрица 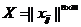– матрица перевозок, – матрица тарифов. План перевозок с минимальной стоимостью называется оптимальным. Бывают такие типы транспортных задач:

1. закрытая транспортная задача – ; (6.9)

2. открытая транспортная задача:

Ÿ с неудовлетворенным спросом ;

Ÿ с неудовлетворенным предложением .

Если имеется транспортная задача открытого типа, то для решения ее необходимо свести к закрытому типу.

В этом случае для задачи с неудовлетворенным предложением вводятся дополнительные пункты назначения , тогда задача будет сформулирована в виде:

. (6.10)

В полученном решении все перевозки в фиктивный пункт назначения принимаются равными нулю, а стоимость перевозки больше стоимости . Аналогично приводится задача с неудовлетворенным спросом, только в этом случае вводится фиктивный пункт отправления.

6.1.5 Определение начального опорного плана

Опорный план – это план перевозок, с которого начинается решение

Сначала ищется произвольный начальный план, обеспечивающий перевозку груза с соблюдением условий ограничений. Затем ищется оптимальный план перевозок путем последовательного улучшения начального плана. Эту задачу можно решать и симплекс-методом, однако решение, в этом случае, затруднено из-за большого количества переменных.

Теорема: Исходя из условия баланса (6.9), ранг матрицы перевозок на единицу меньше числа уравнений ограничений, т.е. . Ранг – число линейно независимых векторов (уравнений). Существует несколько методов построения начального плана. Рассмотрим метод северо-западного угла. В этом методе матрица перевозок начинает заполнятся с первой верхней клеточки:

1. , т.е. если . Здесь – строки, – столбцы. В дальнейшем все элементы первой строки принимаются равными нулю.

.

2. В полученной приведенной матрице опять применяем метод северо-западного угла.

3. Алгоритм останавливается, когда исчерпаны ресурсы a_i и b_j.

 

Например, есть задача:

При решении этой задачи получаем:

Ответ: .

6.1.6 Алгоритм поиска оптимального плана задачи

1. Найти начальный опорный план методом северо-западного угла, при этом число занятых клеток должно быть .

2. Для найденного плана вычисляется значение потенциалов u_i и v_j. Для этого строят систему уравнений для всех клеточек в которых x_ij > 0. Примечание: Поскольку число переменных в уравнениях n + m, а число уравнений , то для решения системы необходимо положить одну из переменных равной нулю.

3. Для каждой клетки начального плана с x_ij = 0 находим величину s_ij = (u_i - v_j) - c_ij. Если окажутся все s_ij меньше нуля, то данный план оптимален, иначе переходим к следующему пункту.

4. Улучшение плана. Среди положительных значений s_ij находим максимальное. Допустим, оно соответствует элементу x_sk и для данной свободной клетки матрицы строится цикл пересчета, который начинается с клетки x_sk и содержит в качестве вершин непустые клетки. Вершинами цикла считаются клетки, в которых меняется направление перемещения, причем точки пересечения линий перемещения к вершинам не относятся. Нумеруем вершины цикла перемещения, начиная с клетки x_sk которой присваивается номер 0. При построении цикла перемещаться можно только по вертикальным и горизонтальным линиям;

5. Среди занятых клеток цикла (пронумерованных) находим клетку, соответствующую минимальному значению x_ij. Производим перемещение груза по вершинам цикла: из всех нечетных вершин вычитается θ, а ко всем четным оно прибавляется. В результате количество груза не изменяется, но он перемещается;

6. Новый полученный план проверяем на оптимальность по условиям п.3 данного алгоритма.

При определении начального плана или в процессе его оптимизации может быть получен вырожденный план. Чтобы избежать зацикливания следует свести задачу к невырожденной, добавив к одной из клеток плана E > 0, соответствующую фиктивной перевозке и решить задачу как невырожденную. В оптимальном плане считать Е = 0. В случае вырожденности начального плана на Е заменяют тот элемент, который требуется для определения значений потенциалов. Для исключения вырожденности при постройке оптимального плана на Е заменяют 0-й элемент, рассматриваемый в цикле.