Теоретические сведения. 4.1.1 Метод множителей Лагранжа

4.1.1 Метод множителей Лагранжа

Функцией Лагранжа для классической задачи МП называется функция

, (4.1)

где m – число уравнений ограничений, – m-мерный вектор. Элементы вектора l, которые находится в функции Лагранжа, называются множителями Лагранжа, – целевая функция, – уравнения ограничений. Данная функция имеет m+n переменных. Для функции Лагранжа получим ее стационарные точки:

, (4.2)

. (4.3)

Подмножество уравнения (4.2) совпадает с системой уравнений ограничений:

.

Тогда в стационарных точках будем иметь, что , т.е. функция Лагранжа совпадает с целевой функцией. Это значит, что если в стационарной точке функция Лагранжа достигает минимума, то и целевая функция достигаем минимума в этой точке с учетом ограничений. Таким образом, можно осуществить переход от задачи на условный экстремум функции к задаче на безусловный экстремум соответствующей функции Лагранжа.

Остается исследовать эти точки на минимум или максимум. Для этого используем производную второго порядка. Если y – скаляр, а не вектор, то вопрос об экстремуме решается следующим образом: если вторая производная меньше нуля, то это максимум; больше нуля – минимум; равна нулю – тогда исследуется третья производная. Значительно сложнее, если y – вектор. В этом случае исследуется квадратичная форма. Если x – n-мерный вектор , то выражение (4.4) называется квадратичной формой. В матричной форме принимает вид (4.5).

, (4.4)

, (4.5)

где a_ij – элементы симметричной матрицы.

В случае определения экстремума в качестве элементов a_ij используются вторые производные:

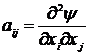. (4.6)

Причем для определения знака квадратичной формы используются определители, составленные из коэффициентов a_ij. Так

D₁= a_ij, (4,7)

. (4.8)

Далее применяют правило: если все определители D₁…D_n – положительны, то квадратичная форма Q_x – положительно определенная и в этом случае имеет место минимум в стационарной точке. Если знаки определителей D₁…D_n чередуются, то квадратичная форма является отрицательно определенной и в стационарной точке имеет место максимум.

4.1.2 Алгоритм метода поиска экстремумов целевой функции с заданными ограничениями

1. По заданному условию задачи (классической задачи оптимизации) составляют функцию Лагранжа.

2. Решая систему уравнений (4.2) - (4.3) находят стационарные точки функции Лагранжа.

3. Проверяют достаточные условия существования экстремума путем исследования знака квадратичной формы.