2018-01-08
746
Два события, происшедшие в различных точках x ₁ и x ₂ системы координат, называются одновременными, если они происходят в один и тот же момент времени во часам в этой системе координат.
В каждой из точек момент события фиксируется по часам, находящимся в соответствующей точке. Будет считать, что события произошли одновременно в неподвижной системе координат в момент t ₀.
В движущейся системе координат эти события произошли в точках x’₁ и x’₂ в моменты t’₁ и t’₂ причем t’₁ и t’₂ являются показаниями часов движущейся системы координат, расположенных соответственно в точках x’₁ и x’₂ этой системы в те моменты, когда в каждой из точек произошло рассматриваемое событие. Связь между штрихованными и нештрихованными величинами дается преобразованиями Лоренца:
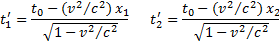
Координаты y z равны 0 т.к. события происходят на оси x. Из полученных уравнений видно, что t’₁ ≠ t’₂, т.е. эти события не одновременны, а происходят с интервалом времени
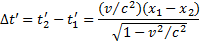
Таким образом, события, одновременные в одной системе координат, оказались неодновременными в другой.
Понятие одновременности не имеет абсолютного значения, независимо от системы координат. Чтобы утверждение об одновременности каких-либо событий имело определенное содержание, необходимо указать, к какой системе координат это утверждение относится.
Чтобы причинно следственная связь имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.
Для доказательства рассмотрим два события в покоящейся системе координат. Пусть событие в точке х₁, происшедшее в момент t₁, будет причиной события в точке х₂ > х₁, происшедшего в момент t₂ > t₁. Скорость передачи «влияния» от точки х₁ к точке х₂ обозначим через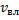 
. Очевидно, по определению скорости имеем
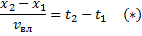
В движущейся системе координат эти события произошли в некоторых точках x’₁ и x’₂ в моменты t’₁ и t’₂. Можем записать
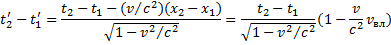
В последнем равенстве величина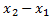 
исключена с помощью (*). Данная формула показывает, что если
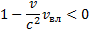
то в движущейся системе координат следствие наступает раньше причины. Но это невозможно, поэтому всегда должно быть
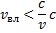
Или
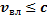
при этом условии причинная связь носит абсолютный характер: не существует системы координат, в которой причина и следствие меняются местами.
