Преобразования Лоренца. Поскольку преобразования Галилея для достаточно больших скоростей приводят к выводам, противоречащим экспериментам

Поскольку преобразования Галилея для достаточно больших скоростей приводят к выводам, противоречащим экспериментам, и постоянство скорости света не является их следствием, они не отражают правильно той связи, которая существует для координат и времени инерциальных систем координат, движущихся друг относительно друга. Преобразования Лоренца – в специальной теории относительности — преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Пусть имеются инерциальные системы отсчета K и K', показанные на рис. На рисунке предполагается, что движется система K', в то время как система K неподвижна. С таким же правом можно считать, что неподвижна система K', а система K движется относительно нее со скоростью — V.

Предположим, что происходит какое-то событие. В системе K. оно характеризуется значениями координат и времени x, у, z, t; в системе K' — значениями координат и времени x', y', z', t'. Найдем формулы связывающие нештрихованные значения со штрихованными. Из однородности пространства и времени следует, что эти формулы должны быть линейными.

При показанном на рис. направлении координатных осей плоскость y' = 0 совпадает с плоскостью y = 0, а плоскость z' = 0 совпадает с плоскостью z = 0. Отсюда вытекает, что, например, координаты y и y' должны обращаться в нуль одновременно, независимо от значений других координат и времени. Это возможно лишь при условии, что

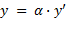
где вследствие линейности уравнения α ‑ постоянная величина. Ввиду равноправности систем K и K' обратное преобразование должно иметь вид

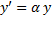
с тем же значением , что и при прямом преобразовании. Перемножив оба соотношения, найдем, что 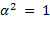, откуда 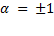. Для одинаково направленных осей нужно взять 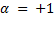. В результате находим, что

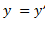или 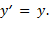(1.104)

Аналогичным образом получается формула

или . (1.105)

Из этих формул вытекает, что значения y и z не зависят от x' и t', откуда следует, что значения x' и t' не могут зависеть от y и z; соответственно значения x и t не могут зависеть от y' и z'. Это означает, что x и t являются линейными функциями только x' и t'.

Из рис. следует, что точка O имеет координату x = O в системе K и в системе K'. Следовательно, выражение 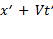должно обращаться в нуль одновременно с координатой x (когда 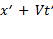равно нулю, ). Для этого линейное преобразование должно иметь вид

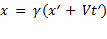, (1.106)

где γ — константа. Точка O имеет координату x' = 0 в системе K' и 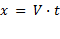в системе K. Следовательно, выражение 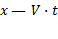должно обращаться в нуль одновременно с координатой x' (когда 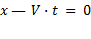, то ). Для этого нужно, чтобы выполнялось соотношение

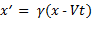. (1.107)

В силу равноправности систем K и K' коэффициент γ в обоих случаях должен быть один и тот же.

Теперь воспользуемся принципом постоянства скорости света. Начнем отсчет времени в обеих системах с того момента, когда начала координат O и O' совпадают. Предположим, что в момент t = t' = 0 в направлении осей x и x' посылается световой сигнал, который производит вспышку света на экране. Это событие (вспышка) характеризуется в системе K координатой x и временем t, а в системе K' — координатой x' и временем t', причем

, .

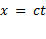(скорость c в обоих случаях одна и та же). Подставив эти значения x и x' в формулы, получим соотношения

,

.

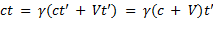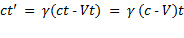Перемножив эти соотношения и сократив обе части получившегося равенства на tt', придем к уравнению

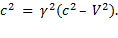
Отсюда 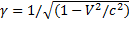, (1.108)

где 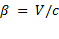. (1.109)

Подстановка найденного значения 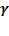в (1.106) и (1.107) приводит к формулам

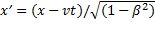, ,. (1.110)

Чтобы найти формулы преобразования времени, исключим из формул (1.110) координату x и разрешим получившееся уравнение относительно t. Затем исключим из формул (1.110) координату x' и разрешим получившееся уравнение относительно t'. В результате придем к формулам

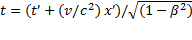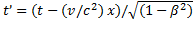,, . (1.111)

Напишем вместе формулы (1.104), (1.105), (1.110) и (1.111), подразделив их на две группы:

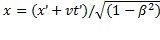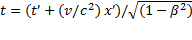, , ,, (1.112)

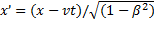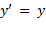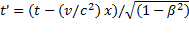,, , ,, . (1.113)

7.Инварианты преобразований Лоренца: пространственно-временной интервал между событиями.

Пусть события произошли в точке x₁ y₁ z₁ в момент времени t₁ и в точке x₂ y₂ z₂ в момент времени t_2. Интервалом этого события называется величина s, квадрат которой определяется формулой:

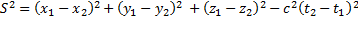. Эта величина имеет во всех системах одно и то же значение, т.е. является лоренц-инвариантной. Произведем преобразования:

=

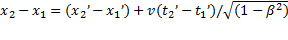
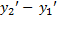
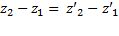
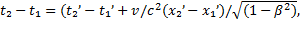отсюда: