2018-01-08
714
Постоянные интегрирования определяются путем подстановки в решение для искомой функции соответствующих начальных условий.
Пусть решение для искомой функции i(t) содержит только одну постоянную интегрирования:
Постоянная интегрирования находится путем подстановки в решение начального условия для самой функции, т.е. i(0): 
Пусть решение для искомой функции i(t) содержит две постоянных интегрирования и имеет вид:
Постоянные интегрирования в этом случае находятся путем подстановки в решение начальных условий для самой функции i(0) и для ее первой производной di/dt(0):
В результате совместного решения этой системы уравнений определяют искомые постоянные интегрирования А1 и А2.
Переходные процессы в последовательной цепи с R,L элементами.
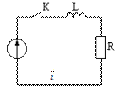Ri+L 
= E
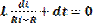
Решим уравнение для тока после коммутации получим: 
свободной составляющей 
принужденной составляющей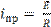 
Свободная составляющая накладывается на принужденную или по существу определяет характер переходных процессов.
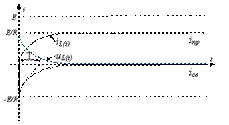
Напряжение в рассмотренной цепи можно определить как
Переходные процессы в последовательной цепи с R,C элементами.
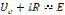
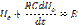
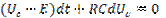
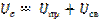
Ток в рассмотренной цепи можно определить как
