Архимедова сила. Уравнение неразрывности. Стационарный поток. Статическое и динамическое давления

 

Архимедова сила. Уравнение Бернулли

В отличие от твердого тела, жидкость — среда бесструктурная, ее микроскопическое устройство не содержит такой «несущей конструкции», как кристаллическая решетка. Соответственно, вопрос об ориентации поверхности, к которой приложено напряжение, здесь не возникает — все ориентации равноправны. Кроме того, в жидкости несравненно меньшую роль играют касательные напряжения. Если в твердом теле они ответственны за сдвиговые деформации и вполне проявляют себя в статике, то в жидкости касательные напряжения возникают исключительно в динамической задаче и лишь при учете диссипативного эффекта — вязкости.

Опыт показывает, что в гидростатике — науке о равновесии жидких тел — а равно и в консервативной (бездиссипативной) гидродинамике существен всего один вид напряжения — давление, обладающее свойством изотропности. Это и составляет содержание закона Паскаля: давление жидкости и газа передается одинаково во всех направлениях. Иными словами, давление — скалярная функция:

P= P(r).(8.18)

Одно из важнейших следствий изотропии давления было известно задолго

до Паскаля — это закон Архимеда: тело, погруженное в жидкость, выталкивается с силой, равной весу вытесненной жидкости. Рассмотрим тело А, плавающее в сосуде с жидкостью (рис. 8.8 а), и отдельно — сосуд, заполненный той же жидкостью до того же уровня, но без погруженного в него тела (рис. 8.8 б). Если жидкость, заполняющая полость а А' на рис. 8.8 б, пребывает в равновесии, то значит силы, действующие на полость А', как раз и

удерживают ее собственный вес. Ввиду скалярности давления (8.18) и отсутствия касательных напряжений, неважно, чем заполнена полость А', так что и на тело А будут действовать так же распределенные силы, имеющие ту же равнодействующую.

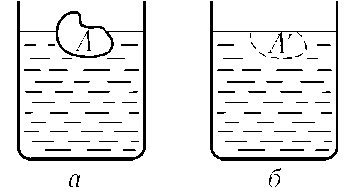Рис. 8.8

Хотя приведенные выше рассуждения и дают нам аргументы в пользу закона Архимеда, они не могут считаться доказательством. В дополнение к ним хотелось бы дать современную трактовку архимедовой силы, пригодную для решения динамических задач. Мы сделаем это, опираясь на закон Паскаля. Пусть давлениие в жидкости или газе зависит от координаты:

P = P(x)

(рис. 8.9). Выделим мысленно в жидкости некоторый параллелепипед со сторонами dx, dy, dz, ориентированными по координатным осям. Тогда в напралении оси х на него будет действовать сила P(x) • dy dz, а навстречу ей —P(x + dx) • dy dz, суммарная же сила будет равна их разности, которая, в силу малости dx, может быть линеаризована:

Fx = P(x) dydz - P(x + dx) • dy dz =

- (dP/dx) • dxdydz + О(х).

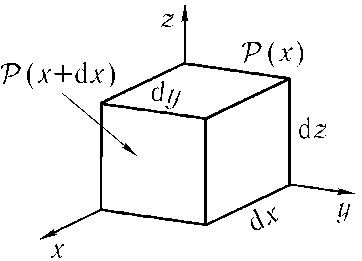
Рис. 8.9

Удобно ввести понятие объемной плотности силы:

fx = dFx/dV = -dP/dx. (8.19)

Это и есть сила Архимеда. В случае зависимости давления от трех координат, вместо обычной производной в (8.19), следует использовать операцию градиента — см. (8.25).

Представим себе, например, несжимаемую жидкость в поле тяжести. При р(х) = const объемная плотность силы тяжести есть просто рg. Пусть ось х направлена вглубь жидкости. Запишем условие равновесия любого малого элемента объема dV:

ρgdV - (dP/dx) • dV = 0.

Сокращая dV и интегрируя, получаем хрестоматийный результат:

P = P0 + ρgх,(8.20)

где Po — давление на поверхности жидкости. Из (8.20) можно получить решение упомянутых выше статических задач. Рассмотрим в качестве примера два открытых сосуда, соединенных посредством сифона (рис. 8.10). Давление жидкости в точке А,

с точностью до отношения ширины трубки к высоте ее над уровнем жидкости в сосудах h, равно

P0 + ρgхА =P0- ρgh,

безоносительно к точке свободной поверхности, от которой мы отсчитываем хА. Тем самым подтверждается, что в сосудах, соединенных так, как показано на рис. 8.10, жидкость в равновесии оказывается на одном уровне, а при нарушении этого условия должно возникнуть течение, перекачивающее жидкость в сосуд с более низким уровнем через трубку. На этом и основан принцип сифона. Рассмотрим эффекты, обусловленные работой давления. Прежде всего представим себе жидкость или газ, занимающие в состоянии равновесия некий цилиндр с площадью основания S (рис. 8.11 а). Давление в пределах данного цилиндрического объема будем считать постоянным и равнымP.

Пусть одно из оснований смещается на малое расстояние dx, но при этом

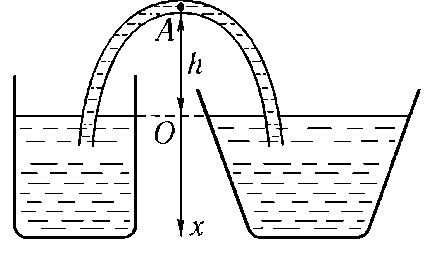
Рис. 8.10 два открытых сосуда, соединенных посредством сифона

количество текучего вещества внутри цилиндра сохраняется, т. е. жидкость

(газ) не течет через движущуюся границу. Сила давления вещества, заполняющего цилиндр, на границу равна P•S, соответственно, работа, совершаемая веществом при расширении, есть

δA = P S dx = P dV,(8.21)

где dV — изменение объема жидкости или газа. Если в процессе расширения

как-то изменится и давление, P—>•P+ d'P, то это даст поправку в (8.21)

всего лишь второго порядка. Пусть теперь слегка меняет объем жидкое или

газообразное тело произвольной формы — на рис. 8.11 б начальное и конечное состояние показаны соответственно сплошной и пунктирной линиями. В силу закона Паскаля,

давление на любой участок границы действует в направлении нормали. Поэтому на любой малой площадочке, принадлежащей границе, мы можем построить цилиндрик с образу-

образующей, параллельной направлению нормали ξ (рис. 8.11 б).

Дальнейшие рассуждения аналогичны выводу (8.21), а затем можно вклад всех цилиндриков просуммировать (с учетом знака!) и получить тот же ответ:

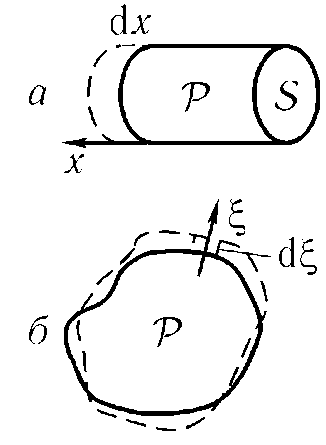Рис. 8.11

δA = P dV

где под dV подразумевается полное изменение объема жидкого элемента.

Рассмотрим стационарное течение жидкости или газабез диссипации. Вы-

Выделим некоторую трубку тока (рис. 8.12).

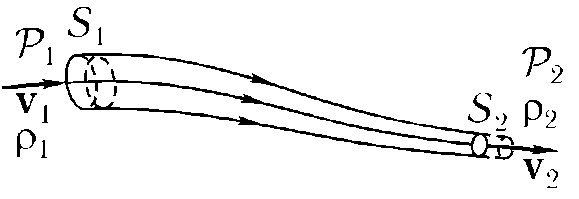
Рис. 8. 12

Пусть S1и S2— два произвольных сечения, нормальных к потоку, ρ1, v1 и ρ2, V2— соответственно, плотность и скорость в сечениях S1и S2. За время dt через сечение S1протек объем S1v1dt, при этом втекающий газ совершил работу Р1S1v1dt. За то же вре-

время из сечения S2вытек объем S2v2dt, совершив при этом работуP2S2v2dt над всем вытекающим газом. При стационарном течении массы ρ2S2v2dt и ρ1S1v1dt, очевидно, равны. Введем плотность энергии текучей среды:

dE/dV = ρε + ρv2/2,

где ε включает отнесенную к единице массы внутреннюю энергию плюс энергию во внешних полях, т. е. всю энергию, кроме кинетической, плотность которой равна ρv2/2. Поскольку мы положили диссипативные эффекты несущественными, используем закон сохранения энергии:

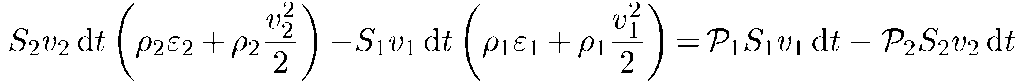
(8.22)

Разделим это уравнение почленно на величину dm протекающей через сечение за время dt массы. Удобно первый член левой части и второй член правой части (8.22) разделить на dm = ρ2S2v2dt, а второй член левой части и первый член правой части (8.22) разделить на dm = ρ1S1v1dt. В результате получаем уравнение Бернулли

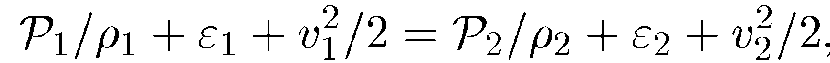
или, что то же,

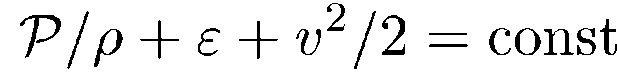
(8.23)

Важный частный случай уравнения Бернулли — течение в поле силы тяжести при неизменной массовой плотности внутренней энергии (для идеального газа это обусловлено постоянством температуры). Тогда

dE/dV = ρgh + ρv2/2,

где h — высота по отношению к некоторому заранее определенному нулевому уровню. Как следствие, получаем

P/ρ + gh + v2/2 = const. (8.24)

Если к тому же, жидкость несжимаема, то (8.24) можно использовать в виде

P + ρgh + pv2/2 = const.(8.25)

Именно эту форму записи чаще всего связывают с именем Бернулли; подчеркнем, однако, что уравнение (8.23) гораздо более универсально.

Уравнение (8.25) позволяет легко получить формулу Торричеллидля скорости вытекания несжимаемой жидкости из сосуда через малое отверстие (она, правда, была выведена за сто лет до уравнения Бернулли). Постановка задачи ясна из рис. 8.13. Пусть высота

уровня воды в сосуде равна h1, а высота, на которой расположено отвестие —h2, так что h1-h2= h. Отверстие должно быть достаточно малым, чтобы выполнялось условие h << v. Из уравнения непрерывности (8.14) легко усмотреть, что для этого необходимо, чтобы

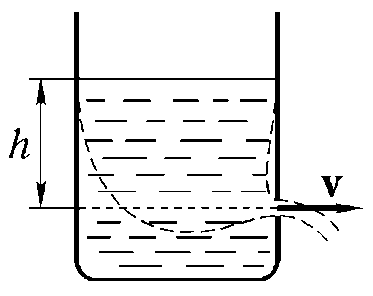
Рис 8 13

сечение отверстия было много меньше сечения сосуда. Таким образом обеспечивается с необходимой точностью, во-первых, стационарность течения и тем самым применимость уравнения Бернулли. Во-вторых, при медленном вытекании мы можем избежать вихревых течений, что позволяет рассматривать наше течение как одну-единственную трубку тока (обозначена пунктиром на рис. 8.13). Это очень важный аспект данной задачи; напомним, что уравнения (8.23)-(8.25) задают инвариант только в пределах трубки тока, который не всегда можно распространить на поток как целое.

Итак, ρ(h1) = ρ(h2), на уровне h1v ~ 0, а на уровнеh2, как следует

из (8.24),

v = √(2gh),(8.26)

т. е. скорость вытекания несжимаемой жидкости из малого отверстия совпадает со скоростью тела, свободно упавшего с высоты h. Это и есть формула Торричелли.

Отметим в заключение, что величина ρv2/2 иногда называется динамическим давлением, а формула (8.25) трактуется как инвариантность суммы статического и динамического давлений. В стационарном потоке несжимаемой жидкости давлениеPдолжно быть меньше там, где больше скорость.

Так объясняют принцип работы пульверизатора, эффект «присасывания» кораблей при близком прохождении параллельными курсами и т. д.

 

Уравнение неразрывности

Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.

Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.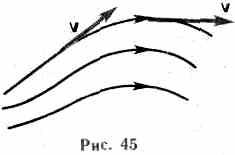

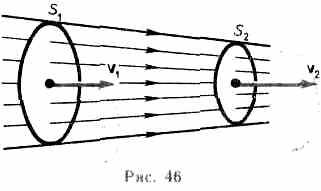
Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 46).

DЗа время t через сечение S проходит объем жидкости SvDt; следовательно, за 1 с через S1 пройдет объем жидкости S1v1, где v1 — скорость течения жидкости в месте сечения S1. Через сечение S2 за 1 с пройдет объем жидкости S2v2,где v2 — скорость течения жидкости в месте сечения S2=const), то через сечениеr. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (S2 пройдет такой же объем жидкости, как и через сечение S1, т. е.

S1v1 = S2v2=const (29.1)

Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (29.1) называется уравнением неразрывности для несжимаемой жидкости.

 

 

24.Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей.

 

 

Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей

Вязкость(внутреннее трение) — это свойство реальных жидкостей оказывать сопротив­ление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявля­ется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медлен­нее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения Fтем больше, чем больше рассматриваемая площадь поверхности слояSD(рис. 52), и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою. На рисунке представлены два слоя, отстоящие друг от друга на расстоянииxи движущиеся со скоростямиv1иv2. При этомv1—v2v. Направление, в котором отсчитывается расстояние между слоями,D=перпендикулярноскорости течения слоев. Величина 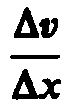показывает, как быстро меняется скорость при переходе от слоя к слою в направлениих,перпендикулярном направле­нию движения слоев, и называетсяградиентом скорости. Таким образом, модуль силы внутреннего трения

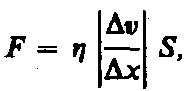(31.1)

где коэффициент пропорциональности m, зависящий от природы жидкости, называетсядинамической вязкостью(или простовязкостью).

с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м×с): 1 Па×Единица вязкости — паскаль-секунда (Па2с/м×с= 1 Н×поверхности касания слоев (1 Па2).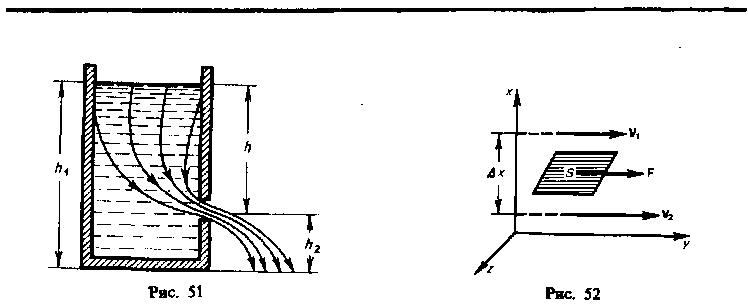

Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей hс увеличе­нием температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Например, вязкость касторового масла в интервале 18—40°С падает в четыре раза. Российский физик П. Л. Капица (1894—1984; Нобелевская пре­мия 1978 г.) открыл, что при температуре 2,17 К жидкий гелий переходит в сверх­текучее состояние, в котором его вязкость равна нулю.

Существует два режима течения жидкостей. Течение называется ламинарным(слоис­тым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, итурбулентным(вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скоро­сти последующих слоев тем больше, чем больше их расстояние до поверхности трубы, и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоро­стей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверх­ности трубы, затем изменяется довольно незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличают­ся. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Профиль усредненной скорости при турбулентном течении в трубах (рис. 53) отличается от параболического профиля при ламинарном течении более быстрым возрастанием скорости у стенок трубы и меньшей кривизной в центральной части течения. Характер течения зависит от безразмерной величины, называемой числом Рейнольдса(О. Рейнольдс (1842—1912) — английский ученый):

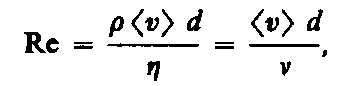
где n = h/p—кинематическая вязкость;р—плотность жидкости; <v>—средняя по сечению трубы скорость жидкости;d—характерный линейный размер, например диаметр трубы.

При малых значениях числа Рейнольдса 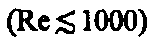наблюдается ламинарное тече­ние, переход от ламинарного течения к турбулентному происходит в област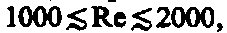и а при 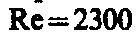(для гладких труб) течение—турбулентное. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков.